外积专题
Numpy 向量化操作加速计算,解决向量外积求和慢的问题
在计算函数二阶导的时候,我们通常需要计算Hessian 矩阵,此时会遇到向量外积求和的问题 ∑ i = 1 n u i v i , u i ∈ R n × 1 , v i ∈ R 1 × n \sum_{i=1}^n u_i v_i, u_i \in \mathbb{R}^{n\times 1}, v_i \in \mathbb{R}^{1\times n} i=1∑nuivi,u
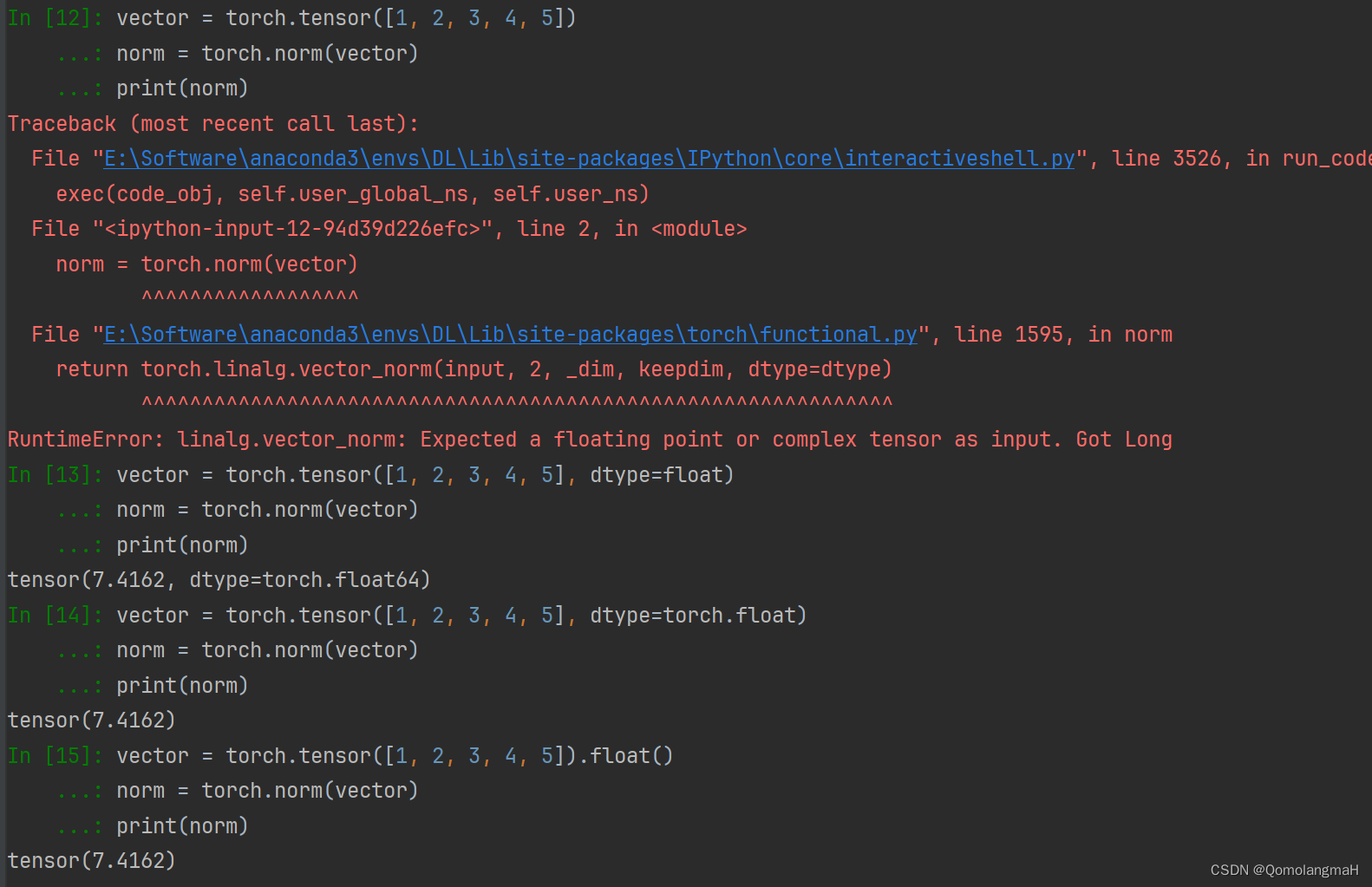
【深度学习】Pytorch 系列教程(三):PyTorch数据结构:2、张量的数学运算(1):向量运算(加减乘除、数乘、内积、外积、范数、广播机制)
文章目录 一、前言二、实验环境三、PyTorch数据结构0、分类1、Tensor(张量)1. 维度(Dimensions)2. 数据类型(Data Types)3. GPU加速(GPU Acceleration) 2、张量的数学运算1. 向量运算a. 简单运算b. 广播操作c. 运算函数加法add乘法mul内积(点积)dot外积(叉积)cross范数norm 一、前言
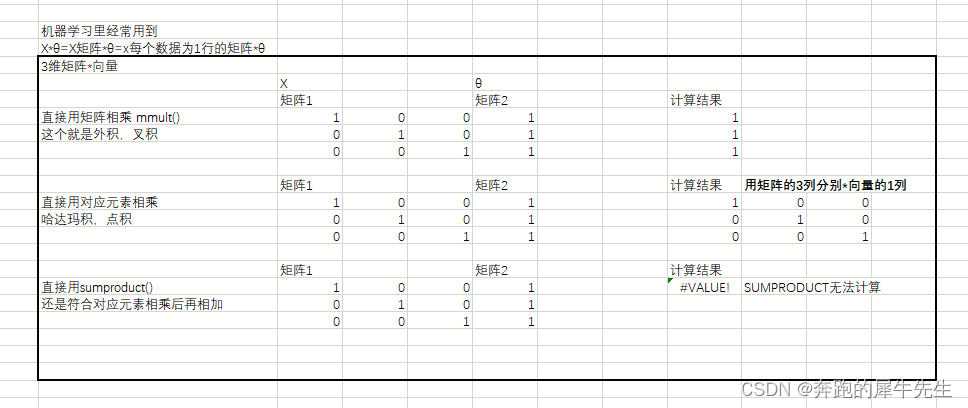
线性代数的学习和整理23:用EXCEL和python 计算向量/矩阵的:内积/点积,外积/叉积
目录 1 乘法 1.1 标量乘法(中小学乘法) 1.1.1 乘法的定义 1.1.2 乘法符合的规律 1.2 向量乘法 1.2.1 向量:有方向和大小的对象 1.2.2 向量的标量乘法 1.2.3 常见的向量乘法及结果 1.2.4 向量的其他乘法及结果 1.2.5 向量的模长(长度) 模长的计算公式 1.2.6 距离 2 向量的各种乘法 2.1 向量的标量乘法(
向量的内积(点乘)与外积(叉乘)
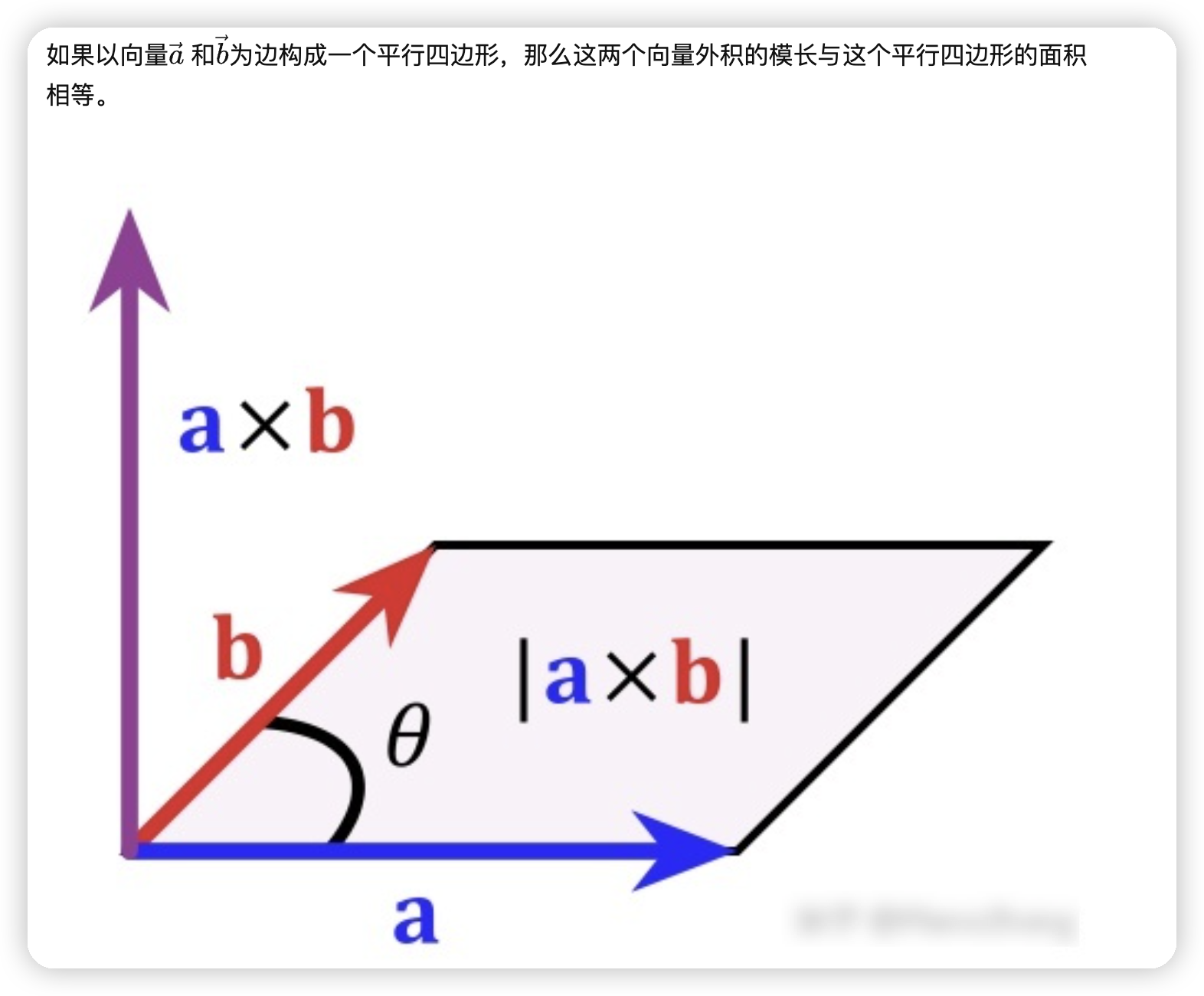
向量的内积(点乘)与外积(叉乘) 向量的内积=点乘 向量的外积=叉乘 向量的内积(点乘) 内积的几何意义: 用来表征或计算两个向量之间的夹角在b向量在a向量方向上的投影。 向量的外积(叉乘) 两个向量的外积,又叫向量积、叉乘等。外积的运算结果是一个向量。并且两个向量的叉积与这两个向量组成的坐标平面垂直(右手定理) 叉乘的几何意义: 向量a和向量b的叉乘结果是一个向量
【数学】 4、向量的内积、外积、模长
文章目录 一、向量点乘(内积)1.1 几何意义1.2 点乘的代数定义,推导几何定义(用于求向量夹角)1.2.1 余弦定理 1.3 程序计算 二、向量叉乘(外积)2.1 几何意义 三、通俗理解内积和外积四、向量的模长 向量点乘、叉乘的概念和意义 一、向量点乘(内积) 点乘(Dot Product)的结果是点积,又称数量积或标量积(Scalar Product)。 1.1
R语言中两个数组(或向量)的外积如何计算
所谓数组(或向量)a和b的外积,指的是a的每一个元素和b的每一个元素搭配在一起相乘得到的新元素.当然运算规则也可自定义.外积运算符为 %o%(注意:百分号中间的字母是小写的字母o).例如: > a <- 1:2> b <- 3:5> d <- a %o% b> d[,1] [,2] [,3][1,] 3 4 5[2,] 6 8 10 注意维数公