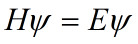哈密顿专题
图论 —— 图的遍历 —— 哈密顿问题
【基本概念】 哈密尔顿通路:经过图中每个结点且仅经过一次的通路。哈密尔顿回路:经过图中每个结点且仅经过一次的回路。哈密尔顿图:存在哈密尔顿回路的图。竞赛图:每对顶点之间都有一条边相连的有向图,n 个顶点的竞赛图称为 n 阶竞赛图。与欧拉回路的对比:欧拉回路是指不重复地走过所有路径的回路;哈密尔顿回路是指不重复地走过所有点并且最后回到起点的回路。 【判定】 1.哈密尔顿通路的判定 设一无向图
hdu 2181 哈密顿绕行世界问题 (深搜)
回朔搜索; #include"stdio.h" #include"string.h" int map[1000][10]; int mark[1000],sum[1000],m,t; void bfs(int x,int s) { int i; if(s==20&&(map[x][1]==m||map[x][2]==m||map[x][3]==m)) {
hdu2181哈密顿绕行世界问题(DFS)
Problem Description 一个规则的实心十二面体,它的 20个顶点标出世界著名的20个城市,你从一个城市出发经过每个城市刚好一次后回到出发的城市。 Input 前20行的第i行有3个数,表示与第i个城市相邻的3个城市.第20行以后每行有1个数m,m<=20,m>=1.m=0退出. Output 输出从第m个城市出发经过每个城市1次又回
哈密顿函数和正则方程
9-2 哈密顿函数和正则方程_哔哩哔哩_bilibili 拉格朗日函数是广义坐标和广义速度的函数 哈密顿函数是广义坐标和广义动量的函数 拉格朗日函数经过勒让德变换得到哈密顿函数
数据结构:哈密顿回路基础
什么是哈密顿回路? 哈密顿回路(Hamiltonian Cycle)是图论中的一个概念,指的是在一个图中通过图的每个顶点恰好一次且仅一次,并最终回到起始顶点的闭合回路。在一个哈密顿回路中,除了起始和结束的顶点必须是同一个顶点,并且这个顶点恰好出现两次之外,其他每个顶点都恰好出现一次。哈密顿回路的命名来自于爱尔兰数学家威廉·罗伊兰·哈密顿。 判断是否存在哈密顿环问题是一个经典的NP完全问题,这意
有趣的安全游戏--哈密顿行动(一)神秘的网页
高高兴兴注册成功后,进来第一题就是一个输入密码的页面 点开查看源码后发现主要逻辑集中在js中,我看到的第一眼简单,随便写了个解密脚本运行得到ORAFEBETLFAEBERFETOLLLRAF然后提交结果显示wrong 难道JS还有隐藏语法这一说?后来才发现下面还有代码 对于这种我果断选择了忽略,那怎么解题呢?想到一种做法,直接将网页源码复制,然后在网页中插入显示密码,如 运
哈密顿算子的计算公式及一些常用公式总结
目录 哈密顿算子的定义式如下: 梯度定义: 散度定义: 旋度定义: 常用的一些公式: 注意文中字母上面没有→的是标量,有→的都表示矢量 哈密顿算子的定义式如下: 快速了解哈密顿算符:数量场(标量场)的方向导数及梯度推导、哈密顿算符定义-CSDN博客 梯度定义: 快速了解梯度:数量场(标量场)的方向导数及梯度推导、哈密顿算符定义-CSDN博客 散度定
HDOJnbsp;nbsp;2181nbsp;nbsp;nbsp;哈密顿绕行世界问题
题目:http://acm.hdu.edu.cn/showproblem.php?pid=2181 有两种代码,感觉都挺好的 #include <iostream> #include <cstring> using namespace std; const int MAXN = 23; bool visit[MAXN]; int n,g,p[MAXN][3],pas[MAXN]; void df
回溯法寻找连通图中是否存在哈密顿回路
使用了回溯法寻找连通图中是否存在哈密顿回路. 哈密顿回路:除了始末点,其他所有点只经过一次 需要注意的地方: ①由哈密顿回路的定义,既然经过了n个点,除了始末两点都不重合,那么这条回路有n条边,在回到初始点前的那一个点处,已经经过了n-1条边 ②起始点start并没有存在数组中,需要手动额外打印 ③一定要记得使用memset初始化 ④检查所有点是否都遍历完的for循环需要放在遍历图的
快乐暑假(八)——欧拉回路和哈密顿回路
欧拉回路 定义 欧拉回路:图G中每条边且只通过一次,并且经过每一顶点的回路 欧拉通路:(欧拉路径):图G中每条边且只通过一次,并且经过每一顶点的通路 欧拉图:存在欧拉回路的图 半欧拉图:存在欧拉通路的图 极大连通子图:在一个连通子图中,包含和顶点有关所有的边(the more the better),那就是极大连通子图。 判定一个图是否是(半)欧拉图 无向图: 定理1:无向图G为欧拉
第十部分 欧拉图与哈密顿图
欧拉图: 历史背景: 哥尼斯堡七桥问题与欧拉图 问题提出后,很多人对此很感兴趣,纷纷进行试验,但在相当长的时间里,始终未能解决。而利用普通数学知识,每座桥均走一次,那这七座桥所有的走法一共有7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040(种)。而这么多情况,要一一试验,这将会是很大的工作量。但怎么才能找到成功走过每座桥而不重复的路线呢?因而形成了著名的“哥尼斯堡七桥
介绍一下TSP问题介绍一下哈密顿回路介绍一下解空间树回溯法解TSP问题时的解空间树为什么是子集树斯德哥尔摩综合征病因临床表现历史记录
目录 介绍一下TSP问题 介绍一下哈密顿回路 介绍一下解空间树 回溯法解TSP问题时的解空间树为什么是子集树 斯德哥尔摩综合征 病因 临床表现 历史记录 介绍一下TSP问题 TSP问题,即旅行商问题(Traveling Salesman Problem),是一个经典的组合优化问题12。它可以描述为:假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每
混沌系统在图像加密中的应用(基于哈密顿能量函数的混沌系统构造1.5)
混沌系统在图像加密中的应用(基于哈密顿能量函数的混沌系统构造1.5) 前言一、自治非哈密顿系统的构造、动态特性分析1.相关理论基础2.两个四维自治非哈密顿系统3.数值分析 python代码 前言 续接混沌系统在图像加密中的应用(基于哈密顿能量函数的混沌系统构造1.4) 一、自治非哈密顿系统的构造、动态特性分析 1.相关理论基础 2.两个四维自治非哈密顿系统
状压DP解决哈密顿回路问题(C/C++实现)
文章目录 一、序言1. 什么是Hamilton图?2. 题目描述 二、为什么可以使用**状压DP**?三、解题思路1.判断是否存在哈密顿路径(状压DP)2.判断是否有哈密顿回路 四、后记 一、序言 1. 什么是Hamilton图? 哈密顿图:图G的一个回路,若它通过图的每一个节点一次,且仅一次,就是哈密顿回路.存在哈密顿回路的图就是哈密顿图. 2. 题目描述 刚看到这个
围棋中的哈密顿算符波函数和能级
薛定谔方程表达的是具有离散特征的运动方程。围棋盘面里只有几百个格子,两个格子之间没有平滑的过渡,不能把棋子下到线上,只能在格子之间跳来跳去.这种运动不是连续的,所以有理由适用薛定谔方程。 H是哈密顿算符,这个算符表达的就是空间和时间对微观粒子运动的约束。具体到围棋盘面,比如把黑棋当作粒子,此时黑棋的运动显然仅受到白旗盘面和围棋规则的约束。因此围棋中的哈密顿算符就是对方的盘面和规则
矩阵对应多项式?多项式?→从特征多项式和哈密顿凯莱定理开始
首先将一个矩阵和一个多项式对应起来(矩阵的多项式,矩阵的零化多项式,相似的矩阵对应零化多项式有相同的最小多项式[https://zhidao.baidu.com/question/273308991.html]) 矩阵与对角化 两个相似的矩阵就是同一个线性映射在两组不同基底下的矩阵;寻找空间 中一个合适的基,使得映射在这个基下对应于一个对角矩阵 空间太大,处理起来麻烦。分解成直和后,就可以先