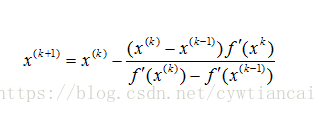图的割点问题 邻接矩阵表示图 package com.hyl.algorithm.other;import java.util.Arrays;import com.hyl.algorithm.search.base.SearchIntf;import com.hyl.algorithm.search.base.SearchIntfFactory;/*** 寻找图的割点* <p>** @aut

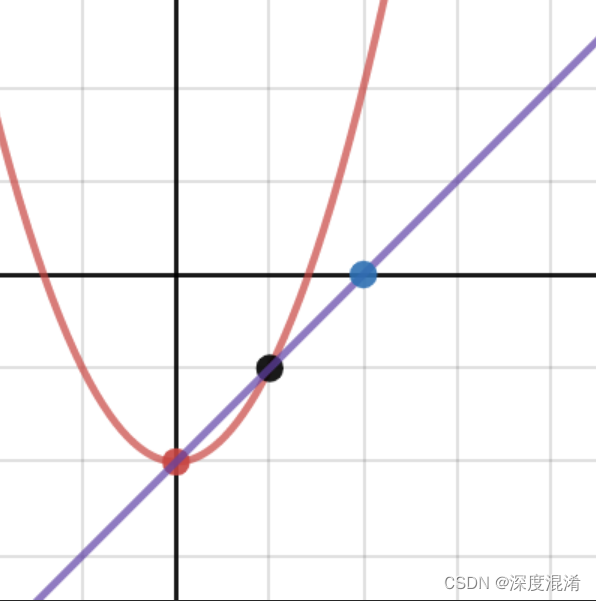
1 割线法 割线法用于求方程 f(x) = 0 的根。它是从根的两个不同估计 x1 和 x2 开始的。这是一个迭代过程，包括对根的线性插值。如果两个中间值之间的差值小于收敛因子，则迭代停止。 亦称弦截法，又称线性插值法.一种迭代法.指用割线近似曲线求方程根的2步迭代法.此法用通过点(xk，f(xk))及(xk-1，f(xk-1))的割线 近似曲线y=f(x)，用割线的根作为方程根

基础介绍： 给定给定区间，函数连续且，那么根据介值定理，函数必然在区间内有根。 二分法：将区间不断二分，使端点不断逼近零点。下一次迭代的区间为或，其中。割线法（线性插值）：基本思想是用弦的斜率近似代替目标函数的切线斜率，并用割线与横轴交点的横坐标作为方程式的根的近似。即给定两个点,。其割线方程为，那么令，x的值即为下一次迭代的结果。逆二次插值法：为割线法的进化版本。使用三个点确定一个二次函数，

1. 基本问题 收敛阶 lim ⁡ k → ∞ ∣ e k + 1 ∣ ∣ e k ∣ r = C > 0 , r 为收敛阶 \lim_{k\to\infty} \frac{|e_{k+1}|}{|e_k|}^r=C>0 \,\,,\,\, r为收敛阶 k→∞lim​∣ek​∣∣ek+1​∣​r=C>0,r为收敛阶 2. 二分法 二分法是线性收敛的，如果指定精度 ϵ { \epsilon

解题思路 定义一个范围和初始点X0，X1 当其迭代公式导数足够小时，我们可以认为此刻的导数已经非常接近于0，为极值点 此时停止循环，得出X代入方程为极小值 割线法的迭代公式： 、 import numpy as npfrom sympy import *eps=0.001def minGX(f,x0,x1):x=Symbol('x')k=0D=1while D>eps:dfx1=d

二分法、试位法、不动点迭代法、牛顿法、割线法 问题回顾问题分析1.二分法2.试位法3.不动点迭代4.Newton-Raphson法5.割线法小结 问题回顾 一段质量均匀分布的电缆线悬挂在两点之间，构成一段悬链，其满足如下微分方程： 问题分析 1.二分法 首先确定有根区间，将区间二等分，通过判断f(x)的符号，逐步将有根区间缩小，直至有根区间足够地小，便可求出满足精