信息论专题
信息论与大数据安全知识点
文章目录 第一章 绪论大数据概述大数据安全与加密技术 安全存储与访问控制技术访问控制概念早期的四种访问控制模型局限性总结 大数据场景下的访问控制技术 安全检索技术密文检索基础 安全处理技术同态加密 隐私保护技术 第一章 绪论 大数据概述 大数据的数据源可以分为 结构化数据 、 非结构化数据 、 半结构化数据 大数据生命周期分为 数据采集 、 数据传输 、 数据存储 、 数
深入理解交叉熵损失CrossEntropyLoss - 信息论(交叉熵)
深入理解交叉熵损失CrossEntropyLoss - 信息论(交叉熵) 信息论 深入理解交叉熵损失CrossEntropyLoss - 信息论(交叉熵)一、自信息(Self-Information)1. 符号取负2. 对数的性质3. 信息的度量数学推导与例子 二、熵(Entropy)的定义例子直观理解熵的性质例子 三、KL 散度由来和意义名字的由来KL 散度的定义直观理解实际应用 四、交
【AI算法岗面试八股面经【超全整理】——信息论】
AI算法岗面试八股面经【超全整理】 概率论信息论机器学习CVNLP 目录 1、自信息、信息熵2、相对熵(KL散度)、交叉熵3、联合熵与条件熵4、互信息 1、自信息、信息熵 自信息 概率与信息量的关系:概率越大的事件,提供的信息量越小;概率越小的事件,信息量越大 信息量计算公式: I ( x ) = − log p ( x ) I(x)=-\log p(x) I(x)=
信息论基础:生日问题
生日问题 我的小学同班同学小琦,和我是同一天生日。每次聚会,我俩同时在场时,我们都会向其他人提起这一点。我们觉得这是很幸运的。 这个概率大吗?要回答这样的问题,需要把几个问题区分清楚。 问题1:对于特定的某个同学,他与我生日相同的概率是多少?这个概率是1/365,并不大。问题2:某班有𝑆个学生,有人与我生日相同的概率是多少?这个概率大约是(𝑆-1)/365,并不小。问题3:某班有𝑆个学
PRML1.6 信息论简介
最近需要比较两个集合的KL散度,特意翻了一下PRML中的相关章节,做个小结。如果不够的化还得翻information theory的书TAT 离散随机变量的信息量 首先从最简单的离散随机变量 X ∈ { x 1 , x 2 , . . . x M } X\in\{x_1,x_2,...x_M\} X∈{x1,x2,...xM}说起,假设 P r ( x i ) = p i Pr(x_i)
【通信原理 入坑之路】—— 信息论部分 线性分组码各种计算的解法
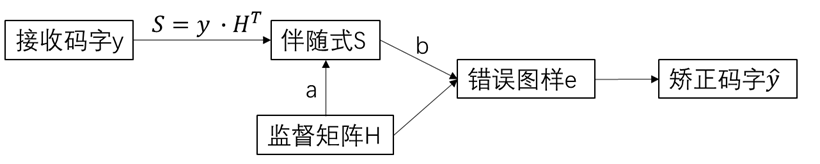
在开始本文之前,我们先给出下面的几个名词,他们将会在后续的分析中反复出现: 【1】生成矩阵 【2】监督矩阵 【3】许用码字 【4】最小汉明距离 【5】伴随式 【6】错误图样 我们先重点看看接收端中,上面这些名词的关联: 首先,当我们接收到码字 y 时,我们可以通过监督矩阵计算出伴随式 S,通过伴随式,我们又可以得到错误图样,错误图样的意义就是它能够指出接收码字中哪一位出错了。从而去修改对应位置
【科研基础|课程】信息论
信息论课程 -上海交大 - 2020春季学期 F:\B\2.sources\CS258信息论 文章目录 1- 信息熵 | 联合熵 | 条件熵 | 链式法则1.1-Entropy 1- 信息熵 | 联合熵 | 条件熵 | 链式法则 P3 信息熵 | 联合熵 | 条件熵 | 链式法则 1.1-Entropy Entropy: Brief History 熵的由来,由热力学
[信息论与编码理论专题-4]:信道、信道模型与信道容量
作者主页(文火冰糖的硅基工坊):https://blog.csdn.net/HiWangWenBing 本文网址:https://blog.csdn.net/HiWangWenBing/article/details/118559972 目录 第1部分 信道的数学模型与分类 第2部分 信道与信道容量 第3部分 离散无记忆信道的信道容量 第4部分 组合信道的信道容量 第5部分 时间
信息论基础:信道模型与信道容量
实际中的信道 信息论是用概率的方法研究信源和信道。前面已经研究了信源的概率模型,现在开始研究信道的概率模型。 首先考虑的是离散信道,它的输入和输出是离散的随机变量。离散信道 Q Q Q是由输入字母表 A X A_X AX、输出字母表 A Y A_Y AY和转移概率矩阵 Q j ∣ i = P ( y = b j ∣ x = a i ) Q_{j|i} = P(y=b_j|x=a_i) Qj
信息论与编码_第五届信息论与编码中大论坛成功举办
2020年8月15日至16日,中山大学数据科学与计算机学院主办,中国电子学会信息论分会、IEEE信息论学会广州分会协办的“第五届信息论与编码中大论坛”通过线上会议成功举办,一百余位专家学者在“云端”共享这场学术盛宴。 本次论坛由中山大学马啸教授、中国电子学会信息论分会主任委员白宝明教授联合主持。 西安电子科技大学耿艳林教授、中国科学技术大学张文逸教授、西安电子科技大学白宝明教授、北京航空航天
信息论与编码_庆祝中山大学计算机科学系成立40周年系列活动 第四届“信息论与编码中大论坛”成功举办...
盛夏的广州,风轻云淡,万物热情似火。白云山下,人才荟萃,庆祝中山大学计算机科学系成立40周年系列活动:第四届信息论与编码中大论坛在广州逸林酒店内顺利进行。 本次论坛议程主要分为两部分:辅导和特邀报告。2019年7月26日是辅导部分,该部分主题为“机器学习与信息论”、“统计学习与编码”,主讲人分别是香港城市大学宋林琦副教授和中山大学马啸教授。 2019年7月27日,中山大学马啸教授向与会嘉宾
【信息论与编码】【北京航空航天大学】实验二、哈夫曼编码【C语言实现】(下)图像编码压缩
实验2 哈夫曼编码(下)(图像编码) 实验简介: 本次实验为实验1:哈夫曼编码的后续补充,实验1见博客:实验一、哈夫曼编码【C语言实现】(上) 说明: 实验代码仅作为学习使用,欢迎转载、改进,禁止用于任何商业用途。 一、实验内容 “不同格式的压缩”: 1、问题: 使用画图软件或者其他工具进行一些简单的艺术创作(推荐使用三四种颜色,不要太多,尽量使用较大的分辨率(例如3840 x 2160
信息论与编码期末复习——计算题+基础汇总(二)
个人名片: 🦁作者简介:一名喜欢分享和记录学习的在校大学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755@qq.com 🦉个人WeChat:Vir2021GKBS 🐼本文由妄北y原创,首发CSDN🎊🎊🎊 🐨座右铭:大多数人想要改造这个世界,但却罕有人想改造自己。 专栏导航: 妄北y系列专栏导航: C/C++的基础算法
信息论与编码期末复习——概念论述简答题(一)
个人名片: 🦁作者简介:一名喜欢分享和记录学习的在校大学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755@qq.com 🦉个人WeChat:Vir2021GKBS 🐼本文由妄北y原创,首发CSDN🎊🎊🎊 🐨座右铭:起点不那么重要,迭代更重要。 专栏导航: 妄北y系列专栏导航: C/C++的基础算法:C/C++是一种常
联合熵与条件熵:信息论中的重要概念探析
在信息论中,联合熵和条件熵是重要的概念,用于描述随机变量的不确定性和信息量。本文将以联合熵和条件熵为主题,从定义、计算方法、应用领域等方面进行探析,帮助读者更好地理解和运用这些概念。 第一部分:联合熵的定义与计算方法 联合熵是指多个随机变量的联合分布的不确定性度量。它表示了在给定所有变量的情况下,所需的平均信息量。联合熵的计算方法可以通过对联合概率分布进行求和和取负数来获得,具体计算公式为:H(
从香农熵到手推KL散度:一文带你纵览机器学习中的信息论
点击上方“中兴开发者社区”,关注我们 每天读一篇一线开发者原创好文 机器之心编译 参与:Nurhachu Null、蒋思源 信息论与信息熵是 AI 或机器学习中非常重要的概念,我们经常需要使用它的关键思想来描述概率分布或者量化概率分布之间的相似性。在本文中,我们从最基本的自信息和信息熵到交叉熵讨论了信息论的基础,再由最大似然估计推导出 KL 散度而加强我们对量
联合基于信息论的安全和隐蔽通信的框架
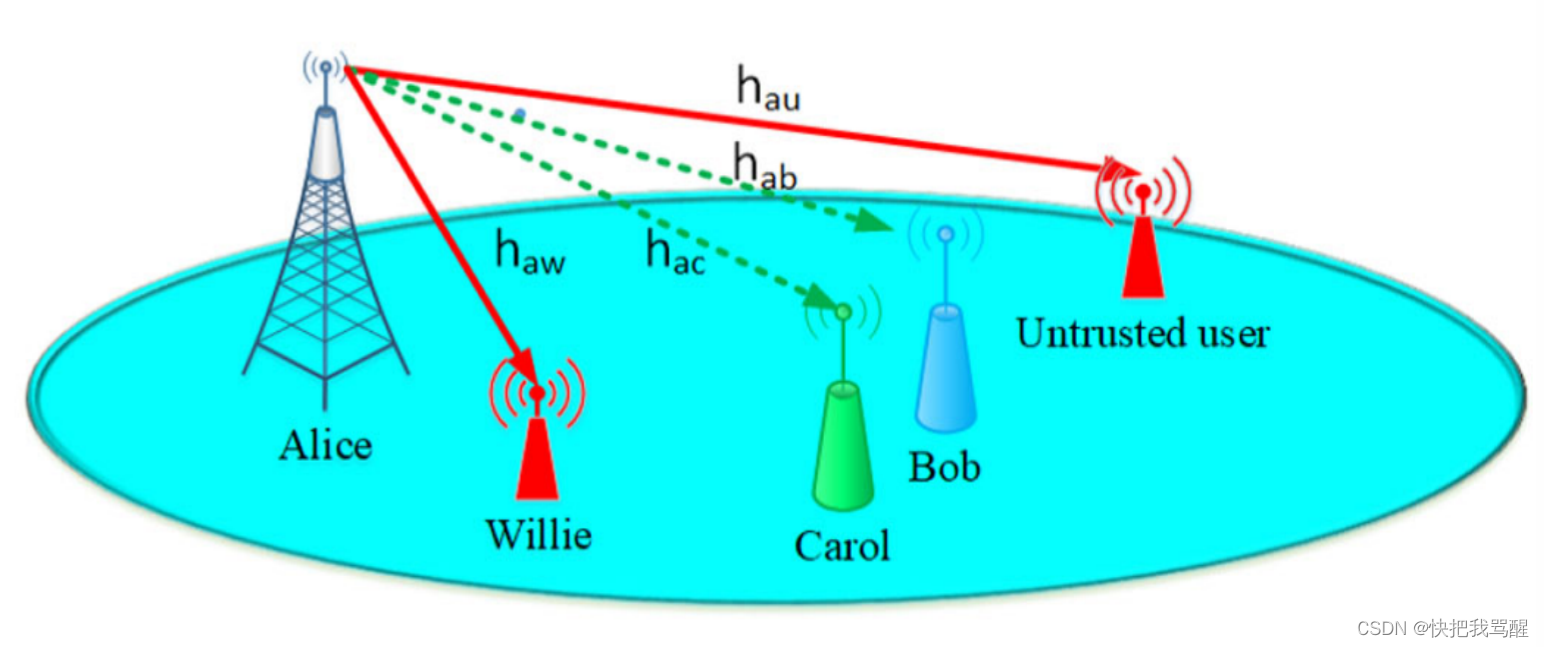
这个标题很帅 abstractintroductionsystem modelPROPOSED JOINT OPTIMIZATION OF ITS AND COVERT TRANSMISSION RATE信息论安全 (ITS)隐蔽通信需要(CC) Joint Information-Theoretic Secrecy and Covert Communication in th
图解AI数学基础(3) | 信息论(要点速查清单·完结)
作者:韩信子@ShowMeAI教程地址:https://www.showmeai.tech/tutorials/83本文地址:https://www.showmeai.tech/article-detail/164声明:版权所有,转载请联系平台与作者并注明出处 信息论是运用概率论与数理统计的方法研究信息、信息熵、通信系统、数据传输、密码学、数据压缩等问题的应用数学学科。信息论中包含的知识
机器学习基础-22:信息论和信息熵
信息论和信息熵 机器学习原理与实践(开源图书)-总目录,建议收藏,告别碎片阅读! 熵的概念最早起源于物理学,用于度量一个热力学系统的无序程度。在信息论里则叫信息量,即熵是对不确定性的度量。从控制论的角度来看,应叫不确定性。信息论的创始人香农在其著作《通信的数学理论》中提出了建立在概率统计模型上的信息度量。他把信息定义为“用来消除不确定性的东西”。在信息世界,熵越高,则能传输越多的信息,熵
《机器学习实战》基于信息论的三种决策树算法(ID3,C4.5,CART)
===================================================================== 《机器学习实战》系列博客是博主阅读《机器学习实战》这本书的笔记也包含一些其他python实现的机器学习算法 github 源码同步:https://github.com/Thinkgamer/Machine-Learning
信息论创始人克劳德·香农:真正的天才是如何思考的?
编者按:克劳德·香农(Claude Shannon),美国数学家、电子工程师和密码学家,被誉为信息论的创始人。1948年,香农发表了划时代的论文《通信的数学原理》,奠定了现代信息论的基础。不仅如此,香农还被认为是数字计算机理论和数字电路设计理论的创始人,也为军事领域的密码分析, 包括密码破译和保密通信,做出了很大贡献。他思考的时候,都从哪些角度入手,又如何得出结论?本文编译自medium原题为“C




![[信息论与编码理论专题-4]:信道、信道模型与信道容量](https://img-blog.csdnimg.cn/20210710161132868.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L0hpV2FuZ1dlbkJpbmc=,size_16,color_FFFFFF,t_70)