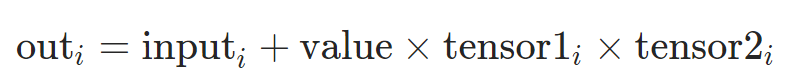之眼专题
毕马威:《智慧之眼:开启汽车感知新时代》
在全球科技飞速发展和产业革新的大潮中,汽车产业正在以前所未有的速度向网联化、智能化的方向转型。汽车传感器作为智能联网汽车发展的关键环节之一,扮演着举足轻重的角色。 毕马威一直关注汽车产业的变化与发展,为了更好地为汽车行业赋能,毕马威中国编写了《智慧之眼:开启汽车感知新时代》。本报告致力于深度探索汽车传感器行业的演进历程,全面解析当下的市场结构与竞争态势。同时,将积极洞察未来行业的主导发展趋势
用上帝之眼进行自动化测试
最近,SIKULI引起很多人的注意。 SIKULI是MIT推出的面向大众的编程语言,也被称为“Picture -Driven Programming”、“图形化编程” 开源主页: http://groups.csail.mit.edu/uid/sikuli/ 官方介绍: Sikuli is a visual technology to search and automa
深度之眼Paper带读笔记NLP.17:GNMT
文章目录 前言第一课 论文导读神经机器翻译简介神经机器翻译相关方法(之前有,看带读15课)多层LSTM模型Attention处理OOV词 前期知识储备 第二课 论文精读论文整体框架模型残差连接双向LSTM束搜索 实验和结果数据集实验结果 讨论和总结 前言 Google’s Neural Machine Translation System:Bridging the Gap be
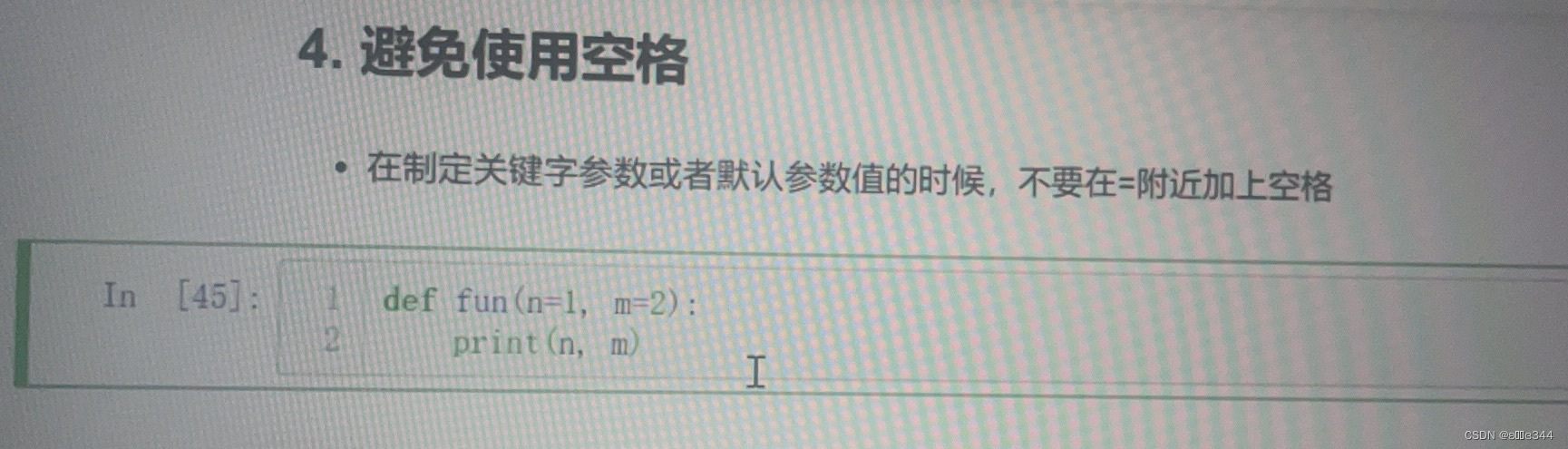
深度之眼(第一节课)Python基础语法元素
一、数据类型 1.1数字类型 int整型 整数float浮点型 带小数的数complex复数 a+bj 1.2字符串类型 用""或者''表达,其中由数字、字母、空格、其他字符等组合而成 1.3布尔类型 两个结果:true、false 2.1组合类型: list列表:[数据有位置顺序]用,分开tuple元组:(元组不可以修改)dict字典:{键:"值"}用键来访问值 ⚠️无序s
深度之眼Paper带读笔记GNN.08.GCN(上)
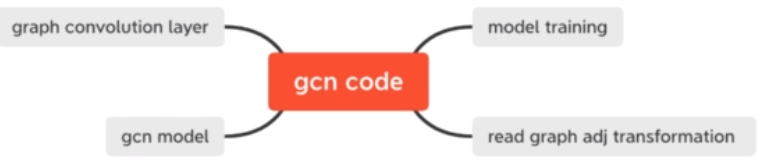
文章目录 前言前期知识基础要求论文结构学习目标研究背景研究意义 泛读摘要论文标题 精读模型总览网上例子原文例子频域和空域Spatial vs Spectral 细节一:R-GCN模型结构细节二:拉普拉斯矩阵Laplacian matrix拉普拉斯算子拉普拉斯矩阵拉普拉斯矩阵的性质拉普拉斯矩阵例子 细节三:图的频域变换图的频域变换Graph spectral图频域变换证明小结 前
深度之眼Pytorch打卡(三):Pytorch张量操作(包括torch.stack()理解、广播(broadcastable)的理解)
前言 张量的操作主要包括张量的形状改变和张量的计算,前者包括张量的拼接(包括torch.stack()理解)、拆分、索引和变换等,后者包括加法、减法,乘加、除加等。本笔记的框架主要来源于深度之眼,并作了一些相关的拓展,拓展内容主要源自对torch文档的翻译和理解。 文中涉及张量创建函数的使用方法见:深度之眼Pytorch打卡(二):Pytorch张量与张量的创建 张量拼接
深度之眼Pytorch打卡(二):Pytorch张量与张量的创建
前言 张量既是Pytorch中的一种基本数据结构,表示多维数组,也是一种自动求梯度的方式。本笔记框架主要来源于深度之眼,并作了一些相关的拓展。内容包括:张量的含义,0维,1维,2维,3维,4维,5维张量的形状;张量的若干参数和自动求梯度的方法;张量的若干常用创建方法。 Pytorch张量 在各种深度学习框架中,张量(tensor)一般是被定义成多维
城市之眼:数据可视化在智慧城市的角色
作为智慧城市建设的核心组成部分,数据可视化扮演着至关重要的角色。在城市中,数据源源不断地产生,涵盖了从交通流量、环境质量到市民需求等各个方面。而数据可视化作为将这些数据呈现出来的手段,对智慧城市的发展起着关键性的作用。我在可视化设计上从业多年,也接手过不少智慧城市的项目,下面就和大家分享一下我对数据可视化在智慧城市项目中作用的看法。 首先,数据可视化为智慧城市提供了深入洞察的方式。通过图
《OpenCv视觉之眼》Python图像处理十五 :Opencv图像处理之图像缩放、旋转和平移原理及实现
本专栏主要介绍如果通过OpenCv-Python进行图像处理,通过原理理解OpenCv-Python的函数处理原型,在具体情况中,针对不同的图像进行不同等级的、不同方法的处理,以达到对图像进行去噪、锐化等一系列的操作。同时,希望观看本专栏的小伙伴可以理解到OpenCv进行图像处理的强大哦,如有转载,请注明出处(原文链接和作者署名),感谢各位小伙伴啦! 前文参考: 《OpenCv视觉之眼》Pytho
深度之眼Paper带读笔记GNN.08.GCN
文章目录 前言前期知识基础要求论文结构学习目标研究背景研究意义 泛读摘要论文标题 精读模型总览网上例子原文例子频域和空域Spatial vs Spectral 细节一:R-GCN模型结构细节二:拉普拉斯矩阵Laplacian matrix拉普拉斯算子拉普拉斯矩阵拉普拉斯矩阵的性质拉普拉斯矩阵例子 细节三:图的频域变换图的频域变换Graph spectral图频域变换证明小结 细节四:卷积核介
深度之眼AI自媒体联合科赛平台银行客户二分类算法比赛参赛经验分享
比赛简介 近段时间参加了"深度之眼"联合"科赛"推出的银行客户二分类算法比赛,在“深度之眼”指导李老师的视频教学指导下,有幸复现出baseline。这里首先感谢平台和李老师。比赛链接:「二分类算法」提供银行精准营销解决方案。 赛题描述 数据集:选自UCI机器学习库中的「银行营销数据集(Bank Marketing Data Set)」 这些数据与葡萄牙银行机构的营销活动相关。这些营销
全平台自动化测试软件的未来王者--上帝之眼( Sikuli )的简介与安装
上面的版权声明真讨厌,又不能修改。此文章在注明出处的情况下可以无限制转发:http://blog.csdn.net/actionwind/article/details/52059731 Sikuli 是美国大名鼎鼎的麻省理工学院一个开发团队所开发的一个自动化测试软件,Sikuli 是一个墨西哥单词,即上帝之眼的意思(将在以后的文章中称之为神眼),它具有以下优点:
尿检设备“智能之眼”:维视智造推出MV-MC 系列医疗专用相机
尿液分析是临床检验的基础常规项目,随着医疗设备的不断发展,尿液分析相关仪器的国产化和自动化程度也进一步提升。2022 年国内尿液分析市场的规模约为 28 亿元,激烈的竞争推动了尿检仪器自动化、智能化升级,在仪器中加入机器视觉、AI 等技术来进一步提高尿液检验效率,已成为行业发展的主流趋势。 为了更好地满足医疗行业的需求,维视智造基于15年来针对尿检这一细分领域的机器视觉技术积淀
深度之眼Kaggle比赛实战项目记录—6—第二周第一节 构建baseline
任务 学习时长:1/6——1/7 任务名称:构建baseline 任务简介:完成一个基本的baseline提交到kaggle上然后有成绩 详细说明: 本节将会向大家介绍利用python数据清洗和数据预处理以及模型的构建,拟合数据,进行对test数据集进行预测,提交到成绩有排名。会先从理论讲起,再到实际的的一个操作。 数据清洗和数据处理是比赛以及任何一种机器学习模型的必须要经过的过程,而
深度之眼吴恩达机器学习课程学习记录——(1)——开营直播
目录 课程目的学习方式课程福利课程安排推荐资料 课程目的 通过近两个月的学习,掌握机器学习基础知识。 学习方式 学习公开课 + 完成作业 + 作业讲解视频 + 答疑 带学讲师 课程福利 打卡返现 对于能坚持到最后,按要求完成全勤打卡且排名前20的,保质保量完成学习的,我们全额返现! 积分活动 课程安排 推荐资料
深度之眼Kaggle比赛实战项目记录—5—第一周【一周学习任务总结】
任务 任务时长:1/5 任务简介: 温故而知新,详细总结回顾本阶段所学习内容,与同学分享自己在学习和作业中遇到的问题。 详细说明: 每第一阶段的学习任务都比较重,第一次学过之后特别容易忘,所以及时做一个要点回顾,会让学习效率大大的提升。 如果复习时还有很多不会的,一定要和小伙伴交流或询问助教和老师,不要把问题留到下一阶段。 打卡截止时间:1/5 打卡内容:图片至少1张,一周总结反思
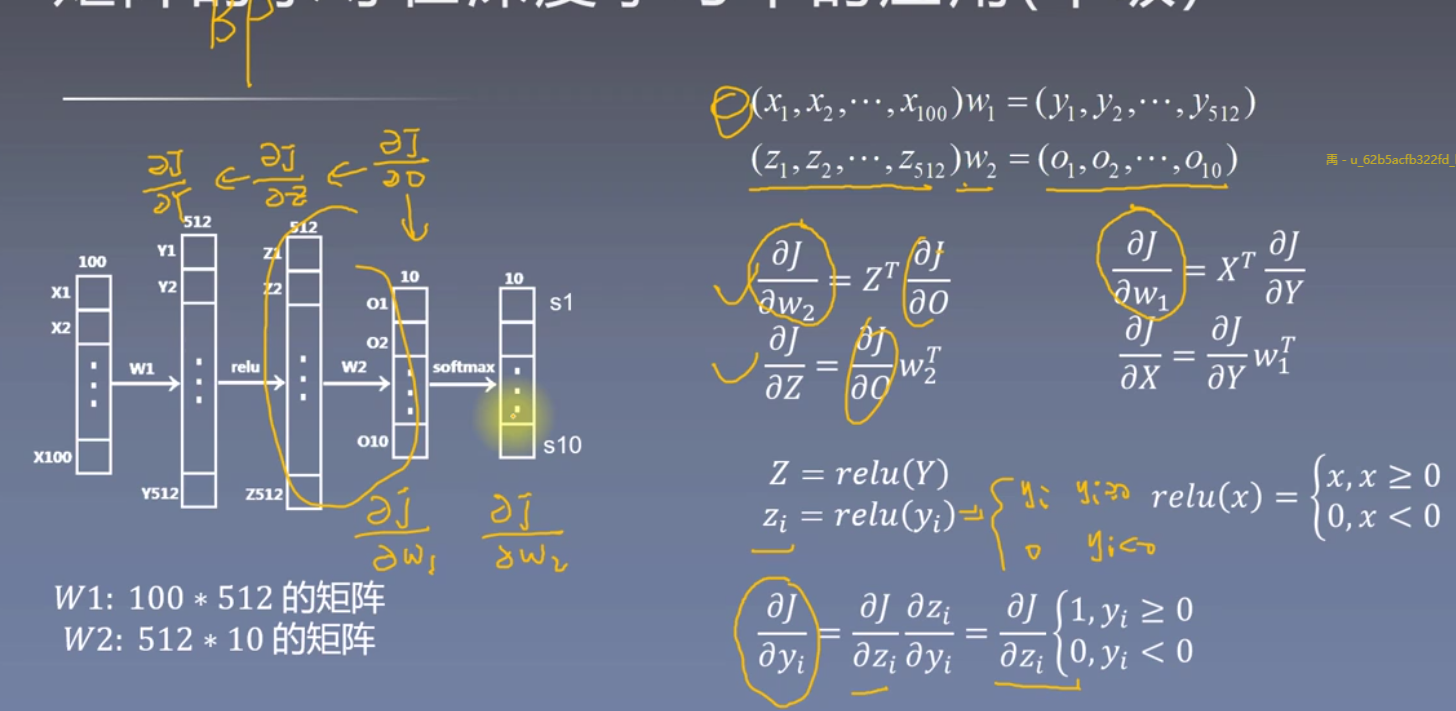
深度之眼(十八)——偏导数与矩阵的求导
文章目录 一、偏导数二、多元复合函数的求导法则,链式求导法则三、方向导数与梯度及其应用四、多元函数泰勒公式与海森炬阵五、多元角数的极值六、距阵的求导七、矩阵的求导在深度学习中的应用 一、偏导数 对某个变量求偏导,则其余变量看成常数 可以直接认为成立,不必拘泥条件 二、多元复合函数的求导法则,链式求导法则 这里举了一个不错的技巧,可以看z到t有几