个泰波专题

1137. 第 N 个泰波那契数

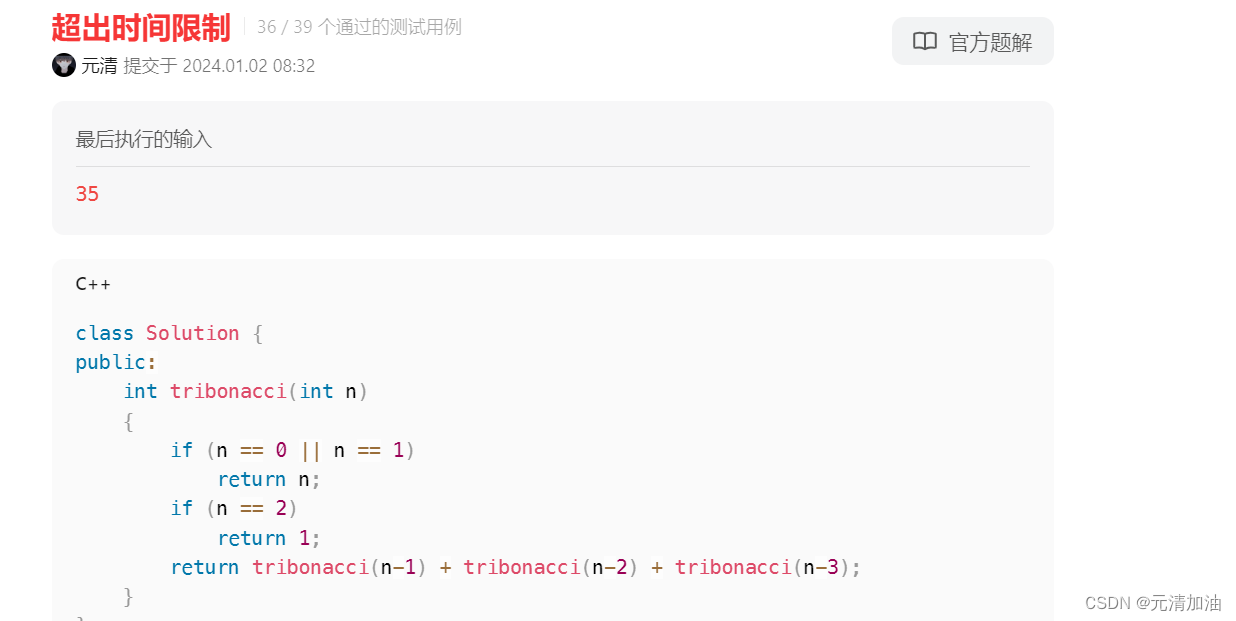
泰波那契序列 Tn 定义如下： T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2 给你整数 n，请返回第 n 个泰波那契数 Tn 的值。示例 1：输入：n = 4 输出：4 解释： T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4 示例 2：输入：n = 25 输出：13895

动态规划1：1137. 第 N 个泰波那契数

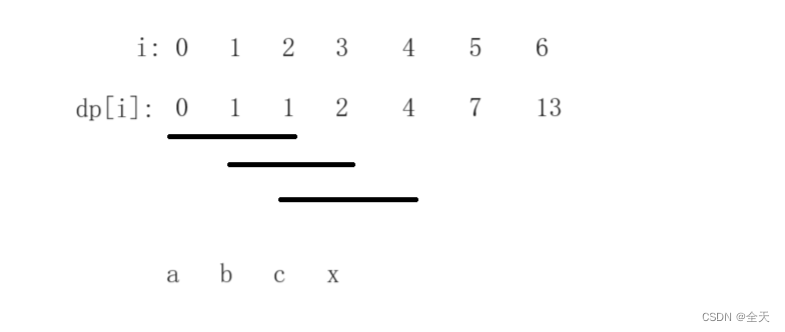
动态规划解题步骤： 1.确定状态表示：dp[i]是什么 2.确定状态转移方程：dp[i]等于什么 3.初始化：确保状态转移方程不越界 4.确定填表顺序：根据状态转移方程即可确定填表顺序 5.确定返回值题目链接：1137. 第 N 个泰波那契数 - 力扣（LeetCode）题解： 1.状态表示：dp[i]表示第i个泰波那契数的值 2.状态转移方程：dp[i]=dp[i-

[Algorithm][递归][斐波那契数列模型][第N个泰波那契数][三步问题][使用最小花费爬楼][解码方法]详细讲解

目录 1.第 N 个泰波那契数1.题目链接2.算法原理详解3.代码实现 2.三步问题1.题目链接2.算法原理详解3.代码实现 3.使用最小花费爬楼梯1.题目链接2.算法原理详解3.代码实现 4.解码方法1.题目链接2.算法原理详解3.代码实现 1.第 N 个泰波那契数 1.题目链接第 N 个泰波那契数 2.算法原理详解题目解析：思路：确定状态表示 -

【力扣】1137. 第n个泰波那契数

原题链接：. - 力扣（LeetCode）目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述泰波那契序列 Tn 定义如下： T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2 给你整数 n，请返回第 n 个泰波那契数 Tn 的值。示例 1：输入：n = 4输出：4

力扣740删除并获得整数和力扣1173第N个泰波那契数

力扣740删除并获得整数给你一个整数数组 nums ，你可以对它进行一些操作。每次操作中，选择任意一个 nums[i] ，删除它并获得 nums[i] 的点数。之后，你必须删除所有等于 nums[i] - 1 和 nums[i] + 1 的元素。开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。示例 1：输入：nums = [3,4,2] 输出：6 解释：删除

【Python】【难度：简单】Leetcode 1137. 第 N 个泰波那契数

泰波那契序列 Tn 定义如下： T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2 给你整数 n，请返回第 n 个泰波那契数 Tn 的值。示例 1：输入：n = 4 输出：4 解释： T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4 示例 2：输入：n = 25 输出：1

斐波那契数列模型-----第N个泰波那契数

1137. 第 N 个泰波那契数 - 力扣（LeetCode）动态规划五个关键点： 1、状态表示：可以理解为dp数组中每一个数dp[i]的含义。怎么得来？（1、题目要求。2、经验+题目要求。3、分析问题的过程中，发现重复子问题。） 2、状态转移方程：即可以认为dp[i] = ？ 3、初始化：怎么样初始化dp表，需要根据状态转移方程和题意来确定。 4、填表顺序：为了填写当前状态的时，要保

每日OJ题_斐波那契dp①_力扣1137. 第 N 个泰波那契数

目录动态规划dp算法原理力扣1137. 第 N 个泰波那契数解析代码1 解析代码2 动态规划dp算法原理动态规划（Dynamic Programming）算法的核心思想是：将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法动态规划算法与分治算法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题

LeetCode刷题--- 第 N 个泰波那契数

个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客个人专栏力扣递归算法题 http://t.csdnimg.cn/yUl2I 【C++】 http://t.csdnimg.cn/6AbpV 数据结构与算法 http://t.csdnimg.cn/hKh2l 前言：这个专栏主要讲述动态规划算法，所以下面题目主要也是这些算

【算法学习】第N个泰波那契数

一、题目描述题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台二、解析题目常规并且简单的动态规划题目，根据动规步骤一步步来即可。动态规划的题围绕着dp表展开的。此题根据题目信息是一个线性的递推过程，一维dp表即可。 1.状态表示对于状态，我的通俗理解是dp表中值的意义或者什么意思。因为我们是要求解第n

动态规划 - 1137.第N个泰波那契数(C#和C实现)

动态规划 - 1137.第N个泰波那契数(C#和C实现) 题目描述泰波那契序列 Tn 定义如下： T0 = 0, T1 = 1, T2 = 1，且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2。给你整数 n，请返回第 n 个泰波那契数 Tn 的值。示例 1: 输入：n = 4输出：4解释：T_3 = 0 + 1 + 1 = 2T_4 = 1

Leetcode#1137:第N个泰波那契数

题目描述泰波那契序列 Tn 定义如下： T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2 给你整数 n，请返回第 n 个泰波那契数 Tn 的值。题解 python3 class Solution:def tribonacci(self, n: int) -> int:# 空间复杂度 O(n）# res = [

动态规划——斐波那契数列模型：1137.第N个泰波那契数

文章目录题目描述算法原理1.状态表示(最重要的）什么是状态表示？状态表示怎么来的呢？本题的状态表示 2.状态转移方程(最难的）本题的状态转移方程 3.初始化(后三步完成剩下百分之一的细节问题）本题的初始化 4.填表顺序本题的填表顺序 5.返回值本题返回值代码实现空间优化题目描述题目链接：1137.第N个泰波那契数算法原理如果我们采用动态规划的思想来解决这道问题

【动态规划】01第 N 个泰波那契数（easy）

题目链接：leetcode第 N 个泰波那契数目录题目解析：算法原理 1.状态表示 2.状态转移方程 3.初始化 4.填表顺序 5.返回值编写代码题目解析：题目让我们求第n个数的泰波那契数。由题可得：我们可以把它改写为：接着我们举几个例子，带入上面的公式来分析：我们可以得到，当我们想得到当前位置的值就需要将前三个位

Leetcode刷题详解——第 N 个泰波那契数

1. 题目链接：1137. 第 N 个泰波那契数 2. 题目描述：泰波那契序列 Tn 定义如下： T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2 给你整数 n，请返回第 n 个泰波那契数 Tn 的值。示例 1：输入：n = 4输出：4解释：T_3 = 0 + 1 + 1 = 2T_4 = 1 + 1

Leetcode刷题详解——第 N 个泰波那契数

1. 题目链接：1137. 第 N 个泰波那契数 2. 题目描述：泰波那契序列 Tn 定义如下： T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2 给你整数 n，请返回第 n 个泰波那契数 Tn 的值。示例 1：输入：n = 4输出：4解释：T_3 = 0 + 1 + 1 = 2T_4 = 1 + 1

[动态规划] (一) LeetCode 1137.第N个泰波那契数

[动态规划] (一) LeetCode 1137.第N个泰波那契数文章目录 [动态规划] (一) LeetCode 1137.第N个泰波那契数题目解析解题思路状态表示状态转移方程初始化和填表顺序返回值代码实现总结空间优化代码实现总结 1137. 第 N 个泰波那契数题目解析解题思路状态表示 (1) 题目要求 (2) 经验+题目要求 (3) 分

【算法挨揍日记】day17——1137. 第 N 个泰波那契数、面试题 08.01. 三步问题

1137. 第 N 个泰波那契数 1137. 第 N 个泰波那契数题目描述：泰波那契序列 Tn 定义如下： T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2 给你整数 n，请返回第 n 个泰波那契数 Tn 的值。解题思路：本题很明显状态表示dp【i】为第n个泰波那契数，本题是第