严谨专题
[思考记录]严谨、讲因果
上周清理罗列了一些程序上的问题,后续又进一步对其中的每一项再次进行了推敲整理。通过整理,帮助逐步还原了某些问题的“真面目”,也让思路更为清晰了。 整理过程(第3步还在进行中): 1、追溯原始问题。为什么会存在这个问题(当时为什么要这样做)、背后想要解决的问题是什么?以此追溯,还原到最开始想要去解决的问题。 2、重新探究解决问题的途径。跳出来,重新审视。因为办法通常不止一种,虽然当
关于thinkPHP3.2中的rewrite不严谨问题会导致网站被注入以及nginx配置中的if多条件判断问题-阿里云阻止指host访问
一、关于thinkPHP3.2中的rewrite不严谨问题会导致网站被注入 thinkPHP3.2的rewrite问题,之前也没在意过,但是今天浏览了一下服务器的一套CMS的相关东西,因为这套CMS是使用thinkPHP3.2搭建的,在浏览代码时发现其目录架构与目前的流行架构不一样,其index.php是写在应用程序的根目录下,而现在的index.php一般都写在public目录(只允许
中点画线中的一些不严谨的地方
我认为对于初学者,特别是自学的人,因为没有老师可以请教,所以任何一点不严谨的地方都会让人困惑很久,我个人认为计算机图学中关于中点画线有如下的不严谨的地方: 1、假设直线的一般方程AX+BY+C = 0,那么A=-(deltaY),B=(deltaX),C=-B(deltaX),这个前提是斜率存在的情况下,但是我见过的老师和教材的讲解,却没有前提,具体推导如下: 假设直线上的两点(x1,y1),
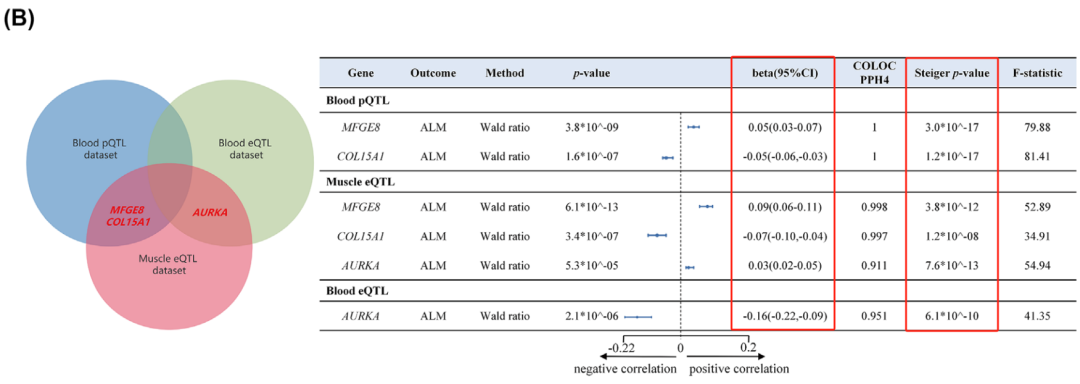
设计严谨,思路绝妙!这篇高级孟德尔随机化研究:药靶、共定位,发文一区(IF=8.9)!...
现在越来越多的学者在用孟德尔随机化高级方法发文,今天我们看的这篇这篇药靶孟德尔随机化,还用了共定位分析方法,亮点在于它的设计严谨,思路绝妙,一起看下去吧! 2024年4月21日,四川大学华西医院陈永平团队做了一项药靶孟德尔随机化研究,在期刊《Journal of CachexiaSarcopenia And Muscle》(医学一区,IF=8.9)发表了题为:“Systematic drugg
leetcode 458. 可怜的小猪 及 题目的不严谨
这道题很有意思,感觉是之前老鼠喝毒药的进阶版,增加了个时间属性,不错解法差不多,主要是看看在测试时间内,有多少批猪死亡,例如:60分钟内,死亡时间为15,则增加了4个状态,则变成了5个状态,所以就要对log(1000) / log(5)上取整,有这么多头猪就可以了。 class Solution {public: int poorPigs(int buckets, int minutesT
抽象模型,严谨代码,开源分享
前言 首先,感谢Eric对我代码上的建议,感谢Stone在FTP Lab环境部署上对我的指导。 今年4月份的时候,做了一个小的项目,当时也没有去总结整理,现在想想总结整理是很有必要的,这也是一个很好的工作研究的习惯。 关于项目,不论大小,其实做到极致也不是一件容易的事。只有做到极致,才算真正的项目经验;只有做到极致,才能让编程真正成为一门艺术;只有体会编
GSC波束形成严谨推导深入细节
GSC广义旁瓣相消器的结构 如下图所示: u ( t ) = x d ( t ) ⋅ a ( θ d ) + ∑ j = 1 M − 1 x j ( t ) ⋅ a ( θ j ) + N ( t ) u(t)=x_{d}(t) \cdot a\left(\theta_{d}\right)+\sum_{j=1}^{M-1} x_{j}(t) \cdot a\left(\theta_{j}\
ThinkPHP5.0.0~5.0.23路由控制不严谨导致的RCE
本次我们继续以漏洞挖掘者的视角,来分析thinkphp的RCE 敏感函数发现 在调用入口函数:/ThinkPHP_full_v5.0.22/public/index.php 时 发现了框架底层调用了\thinkphp\library\think\App.php的app类中的incokeMethod方法 注意传递的参数,ReflectionMethod接受的参数。如果是数组的形式, 那么
严谨的办事态度能减少90%的工作烦恼,避免给公司和团队带来不必要的麻烦
职场生存发展指南包括以下建议: 严谨办事:在工作中,要尽量避免因粗心大意而引起的错误,如忘记投递重要文件或漏办重要事项等。严谨的办事态度能减少90%的工作烦恼,避免给公司和团队带来不必要的麻烦。设定目标:无论是人生目标、阶段性目标还是短期目标,都需要明确并时刻牢记。职场就像一片巨大的原始森林,没有目标的人容易迷失方向。只有那些有明确目标的人,才能在这片森林中找准方向,走出属于自己的成功之路。不要
工业缺陷检测深度学习方法综述——学习笔记(评价:这篇华科大的文章错误百出,学术一点都不严谨,别误人子弟了好吧。。。)
文章目录 摘要1 引言2 问题定义与研究现状2.1 问题定义2.2 问题难点与挑战2.2.1 数据难点2.2.2 任务挑战 2.3 研究概述 3 检测算法3.1 缺陷模式已知3.1.1 传统方法简述3.1.2 深度学习方法 3.2 缺陷模式未知3.2.1 传统方法简述3.2.2 深度学习方法(1) 基于图像相似度的方法(i) 基于图像重建的方法.(ii) 基于图像恢复的方法. (2) 基于特
Struts2 S2-045 漏洞触发流程不严谨推测
// 根据 已有的一些信息和修复版本的代码,推测应该是如下的触发流程// 因为没有测试环境,也只是不严谨的代码触发流程推测,不保证正确性,欢迎大神交流分享。//core\src\main\java\org\apache\struts2\dispatcher\multipart\JakartaMultiPartRequest.javapublic void parse(HttpServletRe
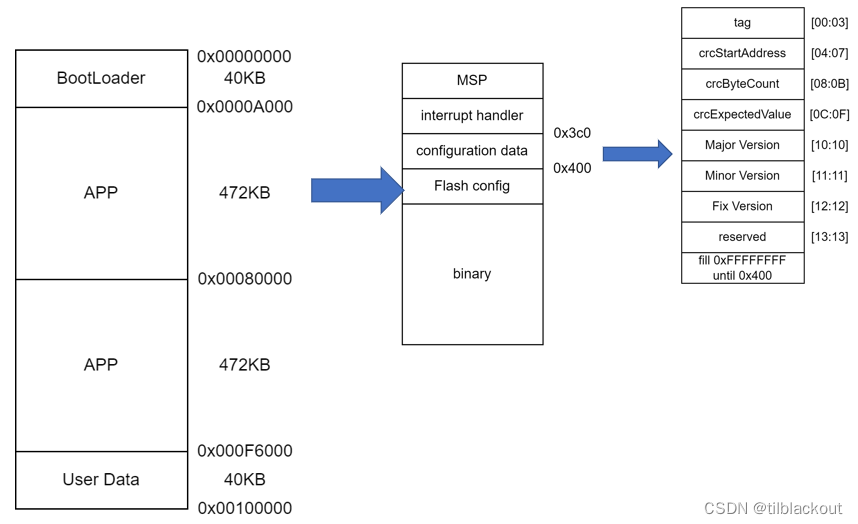
单片机(STM32,GD32,NXP等)中BootLoader的严谨实现详解
Bootloader(引导加载程序)的主要任务是引导加载并运行应用程序,我们的软件升级逻辑也一般在BootLoader中实现。本文将详细介绍BootLoader在单片机中的实现,包括STM32、GD32、NXP Kinetis等等的所有单片机,因为无论是什么样的芯片,它实现的逻辑都是一样的。 注意,本篇文章主要是介绍实现一个严谨的BootLoader需要掌握的基本知识和需要考虑的细节,如果不注意
考研数学/*实验体,每天23:00更新ing~*/洗筋伐髓篇/*数竞*//*此篇内容均可通过严谨的推理与证明以自洽*//*自封为新时代欧几里得《几何原本》之《数研原本》100%推理原创*/
高等数学/*第一篇*/ 第一章: 第一节: Function concept and common function: Introdution: 初等数学与高等数学的区别在于两者的研究对象不同。不变的量->变动的量。计算:方程算的是某个固定的量,而函数算的却是变化的量//初等函数相当于集合中的元素初等数学:四则运算,方程,基本函数,简单几何函数是映射的一种特殊的情况,要理解函数
ROS中/odom,/map,/base_link几个坐标系的含义:从ROS的REP105严谨介绍
这两日看lego-loam,其中的坐标系定义很混乱。 在lego-loam的一个issue中,作者指出他坐标系定义是完全按照ROS的REP103和105的建议的。 然后又看到了关于/odom, /map, /base_link 几个坐标系的含义的说明,因此整理一下。 关于ROS的REP 关于REP:https://ros.org/reps/rep-0000.html The REP con
比较严谨的检验身份证号的真实性与合法性
我们都知道,身份证号是我们每个人的唯一的标识,既然要做到唯一性,身份证号的设计肯定不会仅仅只是设计成18位,最后一位是数字或者“X”这么简单,仅仅只是这么来设计就太low了,而且很容易出现重复的情况,先看看身份证号每一位代表的意思 身份证号码各位数字代表含义 再看看身份证号的校验计算方法 身份证号校验计算方法 1、将前面的身份证号码17位数分别乘以不同的系数。从第一位到
![[思考记录]严谨、讲因果](/front/images/it_default.jpg)