Strassen矩阵乘法简要解析 Strassen矩阵乘法具体描述如下： 两个n×n 阶的矩阵A与B的乘积是另一个n×n 阶矩阵C，C可表示为假如每一个C(i, j) 都用此公式计算，则计算C所需要的操作次数为n3 m+n2 (n- 1) a，其中m表示一次乘法，a 表示一次加法或减法。 为了使讨论简便，假设n 是2的幂（也就是说， n是1，2，4，8，1 6，...）。 首先，假设

机器学习中需要训练大量数据，涉及大量复杂运算，例如卷积、矩阵等。这些复杂运算不仅多，而且每次计算的数据量很大，如果能针对这些运算进行优化，可以大幅提高性能。 一、矩阵乘法 如下图所示： Figure 1 Matrix Multiplication 二、Strassen算法 Figure 2 x^3 vs. x^2.807 三、Strassen原理详解

今天看了strassen算法，用java实现了一下。 另外题目4.2-3，如何修改Strassen算法，使之适应矩阵规模n不是2的幂的情况？ 答：添加额外的行或列使之成为2的幂的方阵，添加的行或列均为0即可。   文章中提到在分解矩阵时使用复杂度为θ(1)的下标运算，本人为了方便，是采用拷贝赋值的方式进行的矩阵分解。   package answers.chapter04;imp

4.2 矩阵乘法，代码如下： //求两个方阵的乘积public static int[][] squareMatrixMultiply(int[][] a, int[][] b){int n = a.length;int[][] c = new int[n][n];for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){c[i][j]

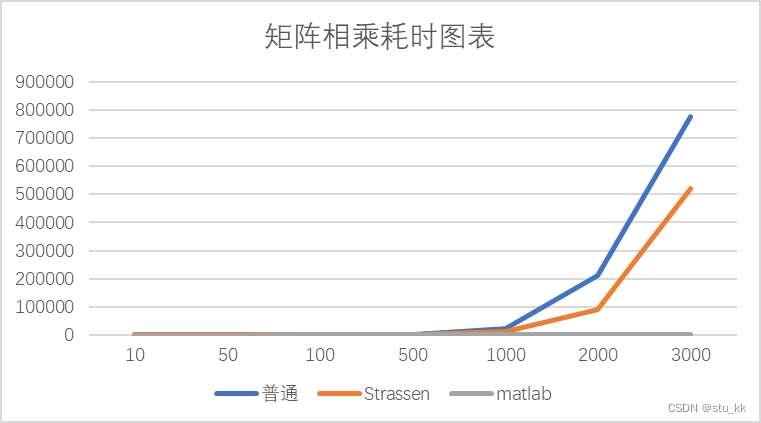
【题目描述】 根据课本“Strassen矩阵乘法”的基本原理，设计并实现一个矩阵快速乘法的工具。并演示至少10000维的矩阵快速乘法对比样例。 【功能要求】 实现普通矩阵乘法算法和“Strassen矩阵乘法”算法对相同的矩阵，分别用普通矩阵乘法算法，“Strassen矩阵乘法”算法和Matlab进行运算，比较时间差异（多次计算求平均值）； 【选做功能】 突破2n的维数限制，能够对其他维数

Volker Strassen 1 矩阵乘法 矩阵乘法是机器学习中最基本的运算之一，对其进行优化是多种优化的关键。通常，将两个大小为N X N的矩阵相乘需要N^3次运算。从那以后，我们在更好、更聪明的矩阵乘法算法方面取得了长足的进步。沃尔克·斯特拉森于1969年首次发表了他的算法。这是第一个证明基本O（n^3）运行时不是optiomal的算法。 Strassen算法的基本思想是将A和B分

引言 Strassen矩阵乘法是一种典型的分治算法。目前为止，我们已经见过一些分治策略的算法了，例如归并排序和Karatsuba大数快速乘法。现在，让我们看看分治策略的背后原理是什么。 同动态规划不同，在动态规划中，为了得到最终的答案，我们需要把一个大的问题“展开”为几个子问题（“expand” the solutions of sub-problems），但是在这里，我们会更多的谈到如何把一

考虑两个 n 级矩阵 A, B, 矩阵 C = A * B. 则有 c i j = ∑ k = 1 n a i j ∗ b k j c_{ij} = \sum_{k=1} ^n a_{ij}*b_{kj} cij​=∑k=1n​aij​∗bkj​. 对于两个矩阵相乘的问题，我们给出三个解决办法：迭代算法、简单分治算法、strassen分治算法。 解法一：迭代算法，即使用三层循环，这是最简单的