本文主要是介绍[算法系列之十五]Strassen矩阵相乘算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
引言
Strassen矩阵乘法是一种典型的分治算法。目前为止,我们已经见过一些分治策略的算法了,例如归并排序和Karatsuba大数快速乘法。现在,让我们看看分治策略的背后原理是什么。
同动态规划不同,在动态规划中,为了得到最终的答案,我们需要把一个大的问题“展开”为几个子问题(“expand” the solutions of sub-problems),但是在这里,我们会更多的谈到如何把一些子解决方案组合到一起。对于一般问题,他们的子问题的解决方案是对等的,他们的归并方式也是通过某种方式定义好的。
一个典型的例子就是归并排序算法。在归并排序中,我们有两个有序数组,我们想要这两个数组在合并之后仍然保持有序。当然了,在归并排序中,最复杂的地方当属自我合并,而原因在于,我们不得不传递两个数组,A和B,然后去比较每一“对”分别来自数组A和数组B的元素。有一点离题,但是,这是归并排序的一个弱点,虽然,它的最坏情况的时间复杂度是 O(n.log(n)),但是,快速排序却往往是实践中更为有效的排序方法,因为,它没有“合并”的过程。快速排序仅仅把两个子数组连接到一起,请注意,在快速排序中,子数组一般并不具有相同的长度,虽然他的最坏时间复杂度是O(n^2),但它的性能却经常好于归并排序。
在上文中,那个简单的例子告诉我们:有时候如何合并两个子问题并不是一个简单的事情。因此,当我们使用分治策略的时候,我们必须非常谨慎。
历史
Volker Strassen是一位出生于1936年的德国数学家。他因为在概率论上的工作而广为人知,但是在计算机科学和算法领域,他却因为矩阵相乘算法而被大部分人认识,这个算法目前仍然是比通用矩阵相乘算法性能好的主要算法之一。
Strassen在1969年第一次发表关于这个算法的文章,并证明了复杂度为n^3的算法并不是最优算法。虽然,事实上Strassen给出的解决方案只会好一点点,但是,他的贡献却是相当巨大的,就是因为这导致了矩阵相乘领域更多的研究,产生了更快的算法,比如复杂度为O(n^2,3737)的Coppersmith-Winograd算法。
概述
两个矩阵 A[NxN] 和 B[NxN] 相乘的通用算法是非常简单的。虽然矩阵相乘比两个数字相乘要复杂得多,而且也不满足交换律,但它仍然非常简单——同时也很慢。
让我们先来定义一下什么是A[NxN]矩阵。当我们提到NxN矩阵,我们首先想到的是一个有N行N列的网格。在每一行和每一列的A[i][j],我们都有一个值。
当然,作为一个开发者,我们会把一个矩阵看成一个二维数组。
int array[][] ={{1,2,3,4},{5,6,7,8},{9,10,11,12}};不要忘记,NxN的矩阵仅仅是任意矩阵中的一种情况,同样的,我们可以有其他任何大小的NxM矩阵(N <> M)。
然而,为了能够和另外一个矩阵相乘,矩阵的大小是非常重要的,为什么?
正如我上面提到的一样,矩阵相乘不同于数字相乘。首先,这个操作不满足交换律。
第二个问题是,让矩阵A和B相乘的方法。
仅仅因为这种方法只对NxN阶矩阵有效,因此我们能看到把矩形矩阵相乘产生的问题(Just because this works with NxN matrices we can see the problem with multiplying rectangular matrices)。确实,如果A矩阵的第二维和B矩阵的第一维不相等,这是不可能的完成的。
不过好在我们现在正在讨论的是具有相同维数的方形矩阵。
好了,现在我们知道如何让两个方形矩阵相乘(具有相同维数NxN),现在,让我们一起去评估一下一般矩阵相乘算法的时间复杂度。
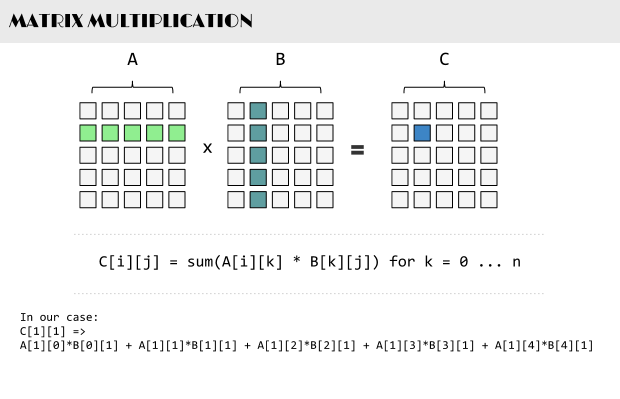
我们知道A.B = C,当且仅当:
C[i][j] = sum(A[i][k] * B[k][j]) for k = 0 .. n于是,我们有一个n^3复杂度的操作。现在,让我们尽力找一个分治策略的算法。
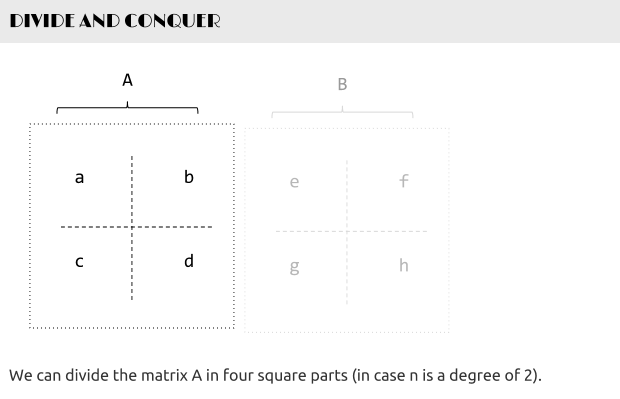
这个对于矩阵来说确实并不难,因为我们知道,一个矩阵可以被分成很多更小的子矩阵。
现在,我们有什么?
再一次,同样的时间复杂度——8个乘积和4个和,那么,计算量在哪?
当然, 为了得到更快的解决方案,我们不得不看一下Strassen在1969做过的工作。他如下图定义了P1, P2, P3, P4, P5, P6 和 P7。
时间复杂度
正如我以上提到的,Strassen算法仅仅比一般矩阵相乘算法好一点点。一般矩阵相乘算法时间复杂度是O(n^3),然而Strassen算法复杂度则是O(n^2.80)。
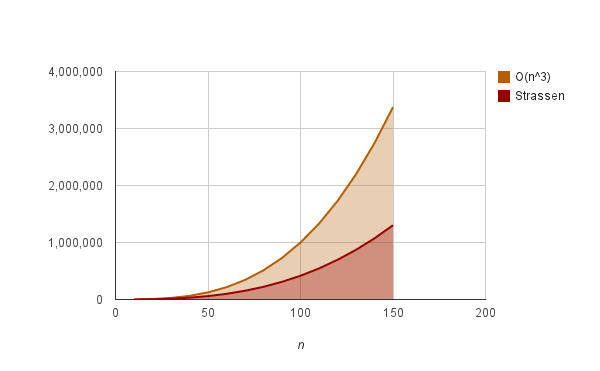
你能在下图观察到,随着n的变大,Strassen算法是如何比一般矩阵相乘算法变得更有效率的。
应用
虽然这个算法看起来更接近纯数学领域,而不是计算机领域。但在实际应用中,任何用到NxN数组的地方,我们都可以从矩阵相乘算法中获益。
另一方面,Strassen算法并不比n^3复杂度的通用矩阵相乘算法快很多。这很重要,因为对于一个很小的n(通常n<45)来说,通用矩阵相乘算法在实践中往往是更好的选择。然而,你可以从以上的图片中看到,对于n>100的情况来说,这两个算法的差别还是相当大的。
同时,当我们谈到|V| = n的邻接矩阵,以及一些依赖矩阵相乘的图论算法的时候,NxN数组经常会在这些领域中使用。
原文链接
Computer Algorithms: Strassen’s Matrix Multiplication
这篇关于[算法系列之十五]Strassen矩阵相乘算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!