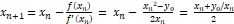sqrt专题

gcc 编译器对 sqrt 未定义的引用

man sqrt Link with -lm. gcc -o test test.c -lm 原因：缺少某个库，用 -l 参数将库加入。Linux的库命名是一致的, 一般为 libxxx.so, 或 libxxx.a, libxxx.la, 要链接某个库就用 -lxxx，去掉头 lib 及 "." 后面的 so, la, a 等即可。常见的库链接方法为

求素数的几个方法（最朴素版、n*sqrt(n)版、埃氏筛、欧拉筛）

最朴素版O(n^2) #include <bits/stdc++.h>using namespace std;int n, cnt, prim[6000000];bool flag; //true 表示质数int main(){scanf("%d", &n);for(int i=2; i<=n; ++i){flag=true; //默认为质数for(int j=2; j<=i-

Pytorch：Tensor基本运算【add/sub/mul/div：加减乘除】【mm/matmul：矩阵相乘】【Pow/Sqrt/rsqrt：次方】【近似：floor...】【裁剪：clamp】

一、基本运算：加减乘除 1、乘法 1.1 a * b：element-wise 对应元素相乘 a * b：要求两个矩阵维度完全一致，即两个矩阵对应元素相乘，输出的维度也和原矩阵维度相同 1.2 torch.mul(a, b)：element-wise 对应元素相乘 torch.mul(a, b)：是矩阵a和b对应位相乘，a和b的维度必须相等，比如a的维度是(1, 2)，b的维度是(1,

c++质数判断使用sqrt

质数判断使用sqrt 如果一个整数能被分解成2个数的乘积，那么小的那个数一定不会超过这个数的开方。使用sqrt函数求解质数不使用sqrt函数求解质数如果一个整数能被分解成2个数的乘积，那么小的那个数一定不会超过这个数的开方。 1不是质数。 8 => 2*4, 4*2 sqrt(8) =>3.xx 9 => 3*3 sqrt(9) =>3 11 => sqrt(11)

undefined reference to 'sqrt'

在gcc下用到数学函数，如sqrt。在gcc时要加上 -lm 参数，这样告诉编译器我要用到数学函数了。如： gcc a.c -o a -lm

求一个正整数N的开方，要求不能用库函数sqrt()，结果的精度在0.001

#include<iostream> using namespace std; int main() { int N; cout<<"输入N的值："; cin>>N double x1 = 1;//初值 double x2 = x1/2.0+N/2.0; while( fabs(x2-x1)>0.001)

【c++leetcode】69. Sqrt(x)

问题入口二分搜索最困难的是能否意识到用二分搜索法解题。算术平方根的区间在[1, x] 。代码如下： class Solution {public:int mySqrt(int x) {if (x == 1 || x == 0){return x;}int64_t start = 1;int64_t end = x;while (start <= x){int64_t mid = s

(LeetCode OJ) Sqrt(x)

题目链接： http://oj.leetcode.com/problems/sqrtx/ 看题目就知道是水题一枚，做这个平台的题目还是没有习惯，毕竟这里的题目都是以面试为目的的，所以Coding的时候一定要谨慎. 这里使用二分查找，二分虽然思路很简单，但是代码还是有几个地方值得注意的，比如 mid = left + (right - left) / 2; 你是不是会使用 mid =

Leetcode: Sqrt(x)

Implement int sqrt(int x). Compute and return the square root of x. 依然二分法….这道题虽然简单，但是有一些细节需要注意，我是提交了好几遍才通过的！参考代码： class Solution {public:int mySqrt(int x) {if (x < 2) return x;int left = 1;int

【NumPy】之常见运算（min、max、mean、sum、exp、sqrt、sort、乘法、点积、对象拼接/切分）

____tz_zs 之前把 numpy 资料写在了同一篇博客里，发现非常难以查阅，于是按功能切分开来。 https://blog.csdn.net/tz_zs/article/details/73929778 https://blog.csdn.net/tz_zs/article/details/80773612 https://blog.csdn.net/tz_zs/article/det

MongoDB聚合运算符：$sqrt

MongoDB聚合运算符：$sqrt 文章目录 MongoDB聚合运算符：$sqrt语法使用举例 $sqrt聚合运算符返回数值的平方根，数值必须为正数，返回值为双精度数。语法 { $sqrt: <number> } <expression>为可解析为非负数的表达式。使用如果参数解析为 null 值或引用缺少的字段，则 $sqrt 返回 null。如果参数解

13,12_基本运算,add/minus/multiply/divide,矩阵相乘mm,matmul,pow/sqrt/rsqrt,exp/log近似值,统计属性,mean,sum,min,max

1.12.基本运算 1.12.1.add/minus/multiply/divide 1.12.2.矩阵相乘mm,matmul 1.12.3.pow/sqrt/rsqrt 1.12.4.exp/log 1.12.5.近似值floor、ceil、trunc、frac、round 1.12.6.现幅max、min、median、clamp 1.13.统计属性 1.13.1.norm 1.13.2.me

【LeetCode】69. Sqrt(x) 二分查找实现开平方函数

题目：翻译：即给定整数x，实现开平方函数。思路： 1.任何大于1的整数的开平方一定是大于1、小于x/2+1的，因此可以在[1,x/2+1]区间内使用二分查找来查找这个数。 2.这个题目还有一个关键问题是，若给定x非常大，计算平方时会溢出，因此数据类型应该设置为long long。题外话：在做这道题的时候，我可以根据x的位数

leetcode69. Sqrt(x)

思路：二分法 class Solution(object):def mySqrt(self, x):""":type x: int:rtype: int""" start=0end=(x+1)/2while(start<end):mid=start+(end-start)/2tmp=mid*midif(tmp==x):return midelif tmp<x:start=mid+1

Java面试题：实现一个sqrt开放函数，指定精度获取结果

面试一面的时候面试官拿出这道题，一开始是懵的，没有什么思路。因为平时一般都用Math.sqrt()函数，很少思考自己怎么实现一个开方函数。思路正难则反，直接求开方没有思路，我们考虑求平方。假设我们要计算5的开方的值，可以依照以下的思路：从1-5之间选择一个值，假设我们选择中值，计算2.5*2.5 = 6.25 > 5那么再从1-2.5中间选择一个值，还是选择中值，计算1.75*

Adagrad求sqrt SGD Momentum Adagrad Adam AdamW RMSProp LAMB Lion 推导

随机梯度下降（Stochastic Gradient Descent）SGD 经典的梯度下降法每次对模型参数更新时，需要遍历所有的训练数据。随机梯度下降法用单个训练样本的损失来近似平均损失。 θ t + 1 = θ t − η g t ( 公式 1 ) \theta_{t+1} = \theta_{t}-\eta g_t (公式1) θt+1=θt−ηgt(公式1) 小批量梯度下降法（

sqrt函数实现（神奇的算法）

我们平时经常会有一些数据运算的操作，需要调用sqrt，exp，abs等函数，那么时候你有没有想过：这个些函数系统是如何实现的？就拿最常用的sqrt函数来说吧，系统怎么来实现这个经常调用的函数呢？虽然有可能你平时没有想过这个问题，不过正所谓是“临阵磨枪，不快也光”，你“眉头一皱，计上心来”，这个不是太简单了嘛，用二分的方法，在一个区间中，每次拿中间数的平方来试验，如果大了，就再试

error C2668: ‘sqrt’ : ambiguous call to overloaded function

转自VC错误:http://www.vcerror.com/?p=1557 问题描述：在把VC6.0 工程转到VS2005工程中遇到下面的问题： error C2668: ‘sqrt’ : ambiguous call to overloaded function 解决方法：具体的解决方法参考文章:http://www.vcerror.com/?p=1557

计算x的平方根x含负数和复数cmath.sqrt(x)

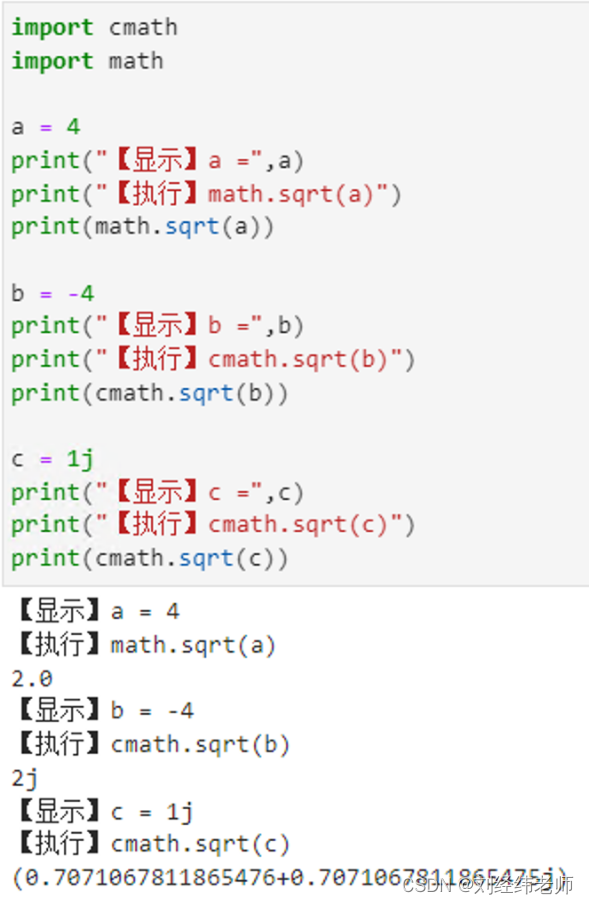
【小白从小学Python、C、Java】【计算机等考+500强证书+考研】【Python-数据分析】计算x的平方根 x含负数和复数 cmath.sqrt(x) cmath.sqrt(-4)输出的结果是？ import cmath import math a = 4 print("【显示】a =",a) print("【执行】math.sqrt(a)") print(math.sqrt(a

平方根(sqrt.pas/c/cpp)（数论）

平方根(sqrt.pas/c/cpp) 【问题描述】给出一个正整数 n (1＜n≤2^31-1)，求当 x,y 都为正整数时，方程的解中， x 最小值为多少？ √n=√x-√y 【输入文件】输入文件只有一行，一个正整数 n。【输出文件】输出文件只有一行，即满足条件的最小 x 的值。【文件样例】 sqrt.in sqrt.out 4 9 【数据规模】 30%的

LeetCode OJ:Sqrt(x)

Sqrt(x) Implement int sqrt(int x). Compute and return the square root of x. 算法思想： 1、二分法 class Solution {public:int sqrt(int x) {if(x < 0) return -1;long long target = (long long

【leetcode】69. Sqrt(x)【M】【74】

Implement int sqrt(int x). Compute and return the square root of x. Subscribe to see which companies asked this question 二分法，最后再加一个处理这么简单的题目竟然才做。。sigh class Solution(o

C++ 实现Sqrt(x)

题目：给你一个非负整数 x ，计算并返回 x 的算术平方根。由于返回类型是整数，结果只保留整数部分，小数部分将被舍去。注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。解题方法一：二分法二分法是我能想到的第一个方法，取两个指针。一个指向最大值一个指向最小值。然后每次循环除二，判断平方数是否大于还是小于输入。直到大的值减去

leetcode刷题69 x的平方根 Sqrt(x)（简单） Python Java

题目大意：实现 int sqrt(int x) 函数。计算并返回 x 的平方根，其中 x 是非负整数。由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。示例 1: 输入: 4 输出: 2 示例 2: 输入: 8 输出: 2 说明: 8 的平方根是 2.82842…, 由于返回类型是整数，小数部分将被舍去。解法一：使用二分查找法，对中间数进行判断，如果

Ubuntu16.04 gcc 编译器对 sqrt 未定义的引用

编译的时候也要在指令后面加 -lm： gcc test.c -lm 原因：缺少某个库，用 -l 参数将库加入。Linux的库命名是一致的, 一般为 libxxx.so, 或 libxxx.a, libxxx.la, 要链接某个库就用 -lxxx，去掉头 lib 及 "." 后面的 so, la, a 等即可。常见的库链接方法为：数学库 -lm; posix 线程 -lpt

数值计算(sqrt函数是怎么实现的)

详细介绍 1. 二分试探法（注意0～1区间的结果比输入要大) 2. 牛顿迭代法：用公式迭代下去；注意反复"震荡"的情况下，要及时终止； 3. 用“割线”，即本点和上一轮点的斜率，来近似函数的导数；速度：牛顿迭代法<割线近似法<<二分试探法还有：梯度下降法，注意有可能遇到导数为0的局部极值；