C++ 实现Sqrt(x)

题目：

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

解题方法一：二分法

二分法是我能想到的第一个方法，取两个指针。一个指向最大值一个指向最小值。然后每次循环除二，判断平方数是否大于还是小于输入。直到大的值减去小的值的差值为1。

class Solution {
public:int mySqrt(int x) {if(x==0)return 0;if(x==1)return 1;//if(x>=9&&x<=15)//    return 3;   long int temp1=pow(2,16);long int temp2=1;int temp;while(temp1-temp2>1){//cout<<"temp1:  "<<temp1<<"temp2: "<<temp2<<endl;if(temp1*temp1==x)return temp1;if(temp2*temp2==x)return temp2;if((temp1*temp1)>x&&(temp2*temp2<x)){//cout<<"(temp1*temp1)>x&&(temp2*temp2<x)"<<endl;temp1=(temp1+temp2)/2;}else if(temp1*temp1<x&&temp2*temp2<x){//cout<<"temp1*temp1<x&&temp2*temp2<x"<<endl;temp2=temp1;temp1*=2;}else if(temp1*temp1>x&&temp2*temp2>x){//cout<<"temp1*temp1>x&&temp2*temp2>x"<<endl;temp1=temp2;temp2/=2;}} if(temp1*temp1==x)return temp1;if(temp1*temp1<x){temp1+=1;if(temp1*temp1>x)temp1-=1;return temp1;}return temp2;     }
};

这里有个小bug。因为是大的数字加小的数字除二之后两者的差值满足一跳出循环，当输入为9时。上值为4下值为1，在该区间内。所以得到新的上值（1+4）/2=2满足上式减下式为一。得到新的上值为2.但其实这时候输出应该为3.所以后面多加了个判断。

官方解答：

class Solution {
public:int mySqrt(int x) {int l = 0, r = x, ans = -1;while (l <= r) {int mid = l + (r - l) / 2;if ((long long)mid * mid <= x) {ans = mid;l = mid + 1;} else {r = mid - 1;}}return ans;}
};

方法二：袖珍计算器算法

「袖珍计算器算法」是一种用指数函数 exp 和对数函数 ln 代替平方根函数的方法。我们通过有限的可以使用的数学函数，得到我们想要计算的结果。

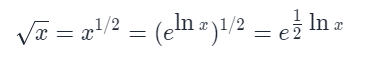
由于计算机无法存储浮点数的精确值（浮点数的存储方法可以参考 IEEE 754，这里不再赘述），而指数函数和对数函数的参数和返回值均为浮点数，因此运算过程中会存在误差。例如当 x=2147395600 时， lnx的计算结果与正确值 4634046340 相差$10^{-11}$
，这样在对结果取整数部分时，会得到 4633946339 这个错误的结果。

因此在得到结果的整数部分ans 后，我们应当找出 ans 与ans+1 中哪一个是真正的答案。

class Solution {
public:int mySqrt(int x) {if (x == 0) {return 0;}int ans = exp(0.5 * log(x));return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans);}
};

方法三：牛顿迭代

牛顿迭代法是一种可以用来快速求解函数零点的方法。

为了叙述方便，我们用 C 表示待求出平方根的那个整数。显然，C 的平方根就是函数

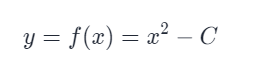
的零点。

牛顿迭代法的本质是借助泰勒级数，从初始值开始快速向零点逼近。我们任取一个$x_0$ 作为初始值，在每一步的迭代中，我们找到函数图像上的点$(x_i,f(x_i))$ 过该点作一条斜率为该点导数$f^{,}(x_i))$ 的直线，与横轴的交点记为 $x_{i+1}$。$x_{i+1}$相较于$x_i$而言距离零点更近。在经过多次迭代后，我们就可以得到一个距离零点非常接近的交点。下图给出了从$x_0$开始迭代两次，得到$x_1$和$x_2$ 的过程。

class Solution {
public:int mySqrt(int x) {if (x == 0) {return 0;}double C = x, x0 = x;while (true) {double xi = 0.5 * (x0 + C / x0);if (fabs(x0 - xi) < 1e-7) {break;}x0 = xi;}return int(x0);}
};

参考：
https://leetcode-cn.com/problems/sqrtx/solution/x-de-ping-fang-gen-by-leetcode-solution/
​