noip2018专题

【NOIP2018普及组复赛】题3：摆渡车

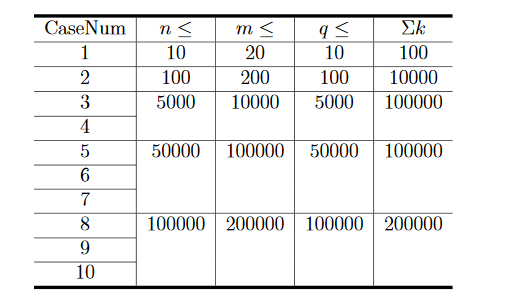
题3：摆渡车【题目描述】有 n n n名同学要乘坐摆渡车从人大附中前往人民大学，第 i i i位同学在第 t i t_i ti分钟去等车。只有一辆摆渡车在工作，但摆渡车容量可以视为无限大。摆渡车从人大附中出发、把车上的同学送到人民大学、再回到人大附中（去接其他同学），这样往返一趟总共花费m分钟（同学上下车时间忽略不计）。摆渡车要将所有同学都送到人民大学。凯凯很好奇，如果他能任意安排摆

【NOIP2018提高组模拟9.20】有所失

文章目录 DescriptionInputOutputSample InputSample Output样例输出1样例输出2 Data ConstraintSolutionCode Description Input Output 若干行，对每个1操作，输出到这个点最多经过多少点。 Sample Input 样例输入1 3 5 1 0 0 1 0 0 1 0 0

【NOIP2018】D2T2 填数游戏

@填数游戏@ @题目描述@@题解@@代码@@end@ @题目描述@ 小 D 特别喜欢玩游戏。这一天，他在玩一款填数游戏。这个填数游戏的棋盘是一个 n×m 的矩形表格。玩家需要在表格的每个格子中填入一个数字（数字 0 或者数字 1 ），填数时需要满足一些限制。下面我们来具体描述这些限制。为了方便描述，我们先给出一些定义：我们用每个格子的行列坐标来表示一个格子，即（

【NOIP2018】D2T1 旅行

@旅行@ @题目描述@@题解@@代码@@end@ @题目描述@ 小 Y 是一个爱好旅行的 OIer。她来到 X 国，打算将各个城市都玩一遍。小Y了解到， X国的 n 个城市之间有 m 条双向道路。每条双向道路连接两个城市。不存在两条连接同一对城市的道路，也不存在一条连接一个城市和它本身的道路。并且，从任意一个城市出发，通过这些道路都可以到达任意一个其他城市。小 Y

【NOIP2018】D1T1 铺设道路

@铺设道路@ @题目描述@@考场上的思路@@比较正常的题解@@end@ @题目描述@ 春春是一名道路工程师，负责铺设一条长度为 n 的道路。铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 n 块首尾相连的区域，一开始，第 i 块区域下陷的深度为 di。春春每天可以选择一段连续区间 [L,R]，填充这段区间中的每块区域，让其下陷深度减少 1。在选择区间时，需要保

CCF NOIP2018复赛获奖名单

2018 NOIP 全套资料下载-提取码：072k 复赛提高组一等奖获奖名单复赛提高组二等奖获奖名单复赛提高组三等奖获奖名单复赛普及组一等奖获奖名单复赛普及组二等奖获奖名单复赛普及组三等奖获奖名单数据来源：全国青少年信息学奥林匹克竞赛官网

[NOIP2018 提高组]保卫王国

保卫王国题解动态dp板子题。首先我们明白，对于一棵树，有最小覆盖集 = 全集 − 最大独立集最小覆盖集=全集-最大独立集最小覆盖集=全集−最大独立集。所以，我们可以将这道题转化成求最大独立集去做，相信最大独立集的方法大家都会，如果不会的话可以看看这里动态dp模板至于必选与不必选的内容，我们可以通过更改点的权值实现，必选就改为 − ∞ -\infty −∞，不

【NOIP2018】【洛谷P5022】旅行【基环树】

题目大意：题目链接：https://www.luogu.org/problemnew/show/P5022 给出一棵 n n n个点 n n n或 n − 1 n-1 n−1条边的图，从任意点开始遍历的方法的字典序。思路：很明显，开始肯定是要在点 1 1 1，这样才能保证字典序最小。建图时要先排序，保证邻接表访问的顺序到达点是升序。也是为了保证字典序最小。然后分类讨论。

备战NOIP2018计划

noip2018提高组初赛是10月13号也就是说有一个月的复习时间重点复习进制转换,常识,数学方法...(买进就算了吧) 复赛是11月10号还有很多没有写我的弱项: 搜索不写挂就是奇迹最基本的剪枝...不熟, 更不要说迭代加深,A*,双向搜索,IDA*... 数学知识暑假自学了一些,但还是不熟,需要巩固重点: 线性筛,扩展欧几里得,乘法逆元,矩阵乘法

$货币系统[完全背包][NOIP2018]$

货币系统[完全背包][NOIP2018]

传送门考场上没有想出来完全背包,写的暴搜dfs 其实f[i]=1 表示i这个价值的货币出现过转移方程 #include<iostream>#include<cstdio>#include<cstdlib>#include<cstring>#include<string>#include<cmath>#include<ctime>#include<cctype>#i

蒟蒻的NOIP2018划水记

前两天晚上，被老师叫走，让学长教育了一波比赛经验(关键)。听完后… …充满斗志，感觉跟喝了大力一样浑身都是力，呵呵。前一天在学校很愉快地写作业到了七点多，接着回到家就累成了狗。吃完饭洗完澡以后，又打开了电脑复习了一下以前做过的题。接着，咳咳…又跑去看番了。十二点就去睡觉了。当天比赛前早上起来，对要比赛的事实，我的内心毫无波澜。准备好东西后，大约11点左右就上车出发了。在

NOIp2018集训test-10-4/test-10-5 (联考四day1/day2)

这个day1稍微有点毒瘤吧？？ DAY1 排列以前总是把day1t1想太复杂了翻车，差不多往正解的方向想了一下感觉不可能这么复杂这可是noipday1t1啊一定有非常简单的方法然后翻车了？？题目转换为求二分图完全匹配数，这个怎么都是十分不好算的，容易想到容斥。用g[i]表示起码选了i条二分图的补图中的边的匹配数。那么答案就是 $ans=\sum_{i=0}^{n}g[i]*(n-i)!*

NOIp2018集训test-10-24（ampm)

李巨连续AK三场了，我跟南瓜打赌李巨连续AK七场，南瓜赌李巨连续AK五场。 DAY1 T1 qu 按题意拿stack,queue和priority_que模拟即可。特判没有元素却要取出的情况。 T2 ming 贪心发现ddl越小的任务越早完成越好，排序更新答案即可。 T3 zi 可能是昨天看了虚树我脑子不太好用，思维僵化的厉害，打算用虚树搞这道题，然后写了180+，连样例都懒得测知道根本过不了交

NOIp2018集训test-10-23

上午考了一套sb题，但是没有人AK。李巨290虐场。下午又考了一套sb题，李巨AK虐场。%%% T1 % 中国剩余定理好像做不了啊，我一直在想如何用CRT做，然后就GG了。然而正解是bike当初说的“CRT根本没用啊你每次合并两个数就可以了”然而这玩意似乎就叫做EXCRT。洛谷模板传送门考虑合并 x=y mod P x=bi mod ai k1*P+y=k2*ai+bi k1*P+k3*

NOIp2018集训test-9-6(am)

Problem A. divisor 发现x为k可表达一定可以表示成这种形式，如k=3,x=(1/3+1/2+1/6)x。于是可以搜索k(k<=7)个1/i加起来等于1的情况，如果一个数是这些i的lcm的倍数这个数就是k可表达的。 std并没有给出它的搜索程序，我的搜索写得很不优秀，所以我写搜索写了很久。一是用double会炸精度，于是我手写了分数类。然后是搜的时候按从大到小搜，每次会有一

NOIp2018集训test-9-22(am/pm) (联考三day1/day2)

szzq学长出的题，先orz一下。 day1 倾斜的线做过差不多的题，写在我自己的博客里，我却忘得一干二净，反而李巨记得清清楚楚我写了的。题目就是要最小化这个东西 $|\frac{y_i-y_j}{x_i-x_j}- \frac{P}{Q}|$ 通分 $\frac{Q*(y_i-y_j)-P*(x_i-x_j)}{Q*(x_i-x_j)}$ 把$Q*x$作为新的$x$,$Q*y-P*x$作为

JZOJ-senior-5921. 【NOIP2018模拟10.21】种花

Time Limits: 2000 ms Memory Limits: 524288 KB Description 院子落叶，跟我的思念厚厚一叠；窗台蝴蝶，像诗里纷飞的美丽章节…… Input 小 H 是一个喜欢养花的女孩子。她买了 n 株花，编号为一里香，二里香……七里香……n 里香，她想把这些花分别种在 n个不同的花盆里。对于一种方案，第 i 个花盆里种的是 ai 里香，小 H

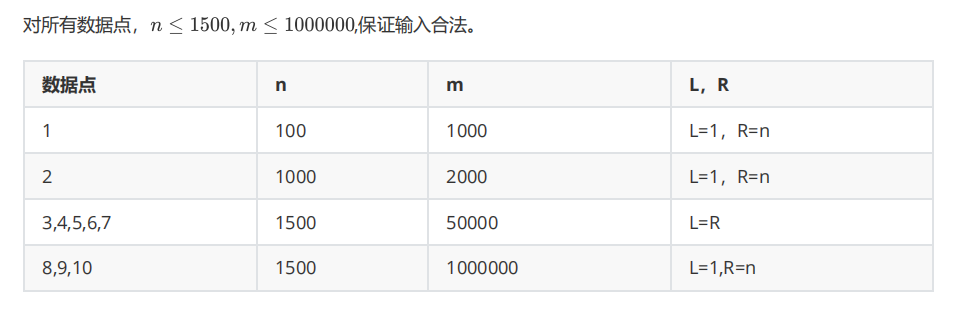
【NOIP2018】洛谷5024 保卫王国

解法一把强制选或者不选点看成对权值的修改，转化成动态最大权独立集问题。树链剖分， f i f_i fi表示 i i i子树的最大权独立集， g i g_i gi表示 i i i子树强制不取 i i i的最大权独立集。 s f i , s g i sf_i,sg_i sfi,sgi表示 i i i轻儿子 f , g f,g f,g的和。如果 u u u是 v v v的重儿子，转移方程为

[JZOJ 5875] [NOIP2018提高组模拟9.20] 听我说，海蜗牛解题报告（BFS+二分）

题目链接： http://172.16.0.132/senior/#main/show/5875 题目: 题解：注意这题只能经过开放的港口我们考虑用vector存下每个点不能到的点，并把并让vector里面的元素升序排序，这样我们就可以二分查找一个点是否与另外一个点相连接下来我们对于每一个开放的港口bfs，每次bfs都把属于这个连通块的港口去掉考虑开两个队列来bfs，队列1存储的是当前

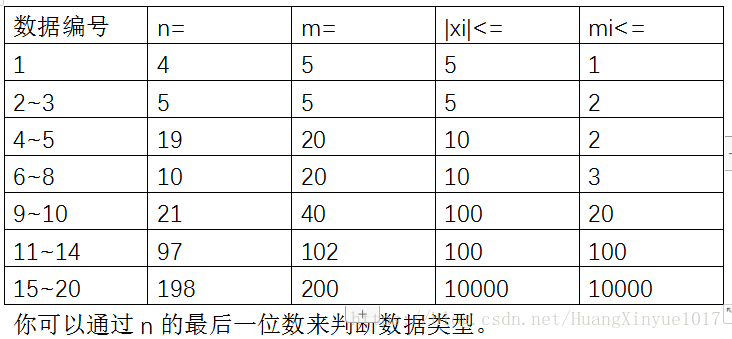
JZOJ5875. 【NOIP2018提高组模拟9.20】听我说，海蜗牛

题解其实想到一种 O ( k 2 ) O(k^2) O(k2)的做法还是比较简单的，枚举两个点有没有边直接相连，用并查集来维护一下。但是对于k比较大的情况下，就应该考虑别的做法。当 k > m k>\sqrt m k>m 的时候，就枚举边，记录一个点不能到达那些点，然后用一个哈希值来表示这个点不能到达点，然后判断不能到达相同点集的点的数量加上不能到达的点集大小是否为n，

NOIp2018集训test-9-18

T1.Conjugate 只能选没选过的点，看成如果选了选过的堆的点就不管它继续选。如果第一次选到某一堆的点在第一次选到第一堆的点之前，这一堆对答案就会有1的贡献。那么a[i]有贡献的概率是a[i]和a[1]的相对顺序序列中，第一个是a[i]中的点的概率（转换后的游戏和原游戏等价），即ai/(a1+ai)，答案就是这个东西求和再+1。 1 //Achen 2 #include<bits

JZOJ-senior-5917. 【NOIP2018模拟10.20】moon

Time Limits: 2000 ms Memory Limits: 524288 KB Description 作为申国的学者，你需要严格遵守三大基本原则：战争即和平自由即奴役无知即力量你正在对一本书进行审核，其中片段写道： “少焉，月出于东山之上，徘徊于斗牛之间。白露横江，水光接天。纵一苇之所如，凌万顷之茫然。浩浩乎如冯虚御风，而不知其所止；飘飘乎如遗世独立，羽化而登仙。” 这种

NOIP2018模板总结【数学】

质因数分解 //质因数分解int prime[MAXN], tim[MAXN], cnt;void Divide(int N){printf("%d = ", N);for(int i = 2; i * i <= N; i++) if(N % i == 0){prime[++cnt] = i;while(N % i == 0) N /= i, tim[cnt]++;}if(N > 1) p

【JZOJ5947】【NOIP2018模拟11.02】初音未来（miku）（逆序对排序+线段树）

Description Hercier作为一位喜爱Hatsune Miku的OIer，痛下决心，将Vocaloid买回了家。打开之后，你发现界面是一个长为n的序列，代表音调，并形成了全排列。你看不懂日语，经过多次尝试，你只会用一个按钮：将一段区间按升序排序。不理解音乐的Hercier决定写一个脚本，进行m次操作，每次对一段区间进行操作。可惜Hercier不会写脚本，他找到了在机房里的你，请你模拟

JZOJ-senior-5947. 【NOIP2018模拟11.02】初音未来（miku）

Time Limits: 1000 ms Memory Limits: 524288 KB Description Hercier作为一位喜爱Hatsune Miku的OIer，痛下决心，将Vocaloid买回了家。打开之后，你发现界面是一个长为n的序列，代表音调，并形成了全排列。你看不懂日语，经过多次尝试，你只会用一个按钮：将一段区间按升序排序。不理解音乐的Hercier决定写一个脚本，进行

前行记录 - NOIP2018游记

NOIP2018游记 - 前行记录 NOIP2018 完跪……滚回学校考半期 QwQ 这篇不是题解 awa ，题解之后会发布的，毕竟我还没有AC呢又及……G2020 陌路笙歌 - 再见(╯▽╰) 感悟第一次考提高组，之前和将要AFO的G2020一起培训了很久，感触颇深~毕竟距离AFO就只剩两年了，还是抓紧吧星期五试机的时候有一点爆炸……O(nlogn) 的最长上升子序列都写挂了。