JZOJ-senior-5921. 【NOIP2018模拟10.21】种花

本文主要是介绍JZOJ-senior-5921. 【NOIP2018模拟10.21】种花，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Time Limits: 2000 ms Memory Limits: 524288 KB

Description

院子落叶，跟我的思念厚厚一叠；窗台蝴蝶，像诗里纷飞的美丽章节……

Input

小 H 是一个喜欢养花的女孩子。

她买了 n 株花，编号为一里香，二里香……七里香……n 里香，她想把这些花分别种在 n个不同的花盆里。

对于一种方案，第 i 个花盆里种的是 ai 里香，小 H 定义其美丽值为：
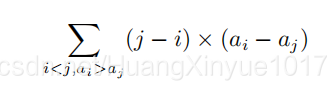
在这里插入图片描述

第一行一个整数 n，第二行有 n 个整数表示 {pi}。pi表示第i个花盆里不可以种ai里香

Output

一个整数，表示答案对 109 + 9 取模的结果。

Sample Input

3
2 1 3

Sample Output

Data Constraint

对于 30% 的数据，n ≤ 16。
对于 60% 的数据，n ≤ 100。
对于 100% 的数据，n ≤ 5000，{pi} 是一个排列。

Solution

这题嘛，DP啊……菜鸡的我只会写暴力
设 $f_{i,j}$ 表示一共有 $(i + j)$ 个元素，其中 $i$ 个元素有位置上的限制， $j$ 个元素没有位置限制
有限制指的假定待放入元素为 $x$ ，存在位置 $p_k=x$ ，而第 $k$ 个位置还没有填入元素
这样我们就有转移式
$f_{0,0}=1，f_{1,0}=0，f_{0,1}=1，f_{0,2}=2$
$f_{x,0}=(x-1)(f_{x-1,0}+f_{x-2,0})$ ……A
$f_{x,y}=x*f_{x-1,y}+y*f_{x,y-1}$ ……B
A式就是错排公式，这里的推导过程简单清晰又自然
B式

然后我们分情况讨论
$i$ 在 $p_j$ 上， $j$ 在 $p_i$ 上，有 $f_{n-2,0}$ 种情况，贡献值为 $a1=max(0,p_j-p_i)$
上面情况只满足一个，有 $f_{n-3,1}$ 种情况，贡献值为 $a2=(\sum{_{k=1}^{p_j-1}}k+\sum{_{k=1}^{n-p_i}}k)-2*a1$
（分别考虑 $j$ 在 $p_i$ 和 $i$ 在 $p_j$ 的情况减去 $i, j$ 同时在 $p_j,p_i$ 的情况）
两个条件都不满足，有 $f_{n-4,2}$ 种情况，贡献值为 $\sum{_{i=2}^n\frac{i*(i-1)}{2}}-a1-a2-\sum{_{k=1}^{p_i-1}k}-\sum{_{k=1}^{n-p_j}k}+max(0,p_i-p_j)$
所以答案为 $\sum{_{j>i}(j-i)*(a1*f_{n-2,0}+a2*f_{n-3,1}+a3*f_{n-4,2})}$

Code

#include<algorithm>
#include<cstdio>#define fo(i,a,b) for(int i=a;i<=b;++i)
#define fd(i,a,b) for(int i=a;i>=b;--i)
#define ll long long using namespace std;const int N=5010,P=1e9+9;
int n,p[N];
ll f[N][3];int main()
{freopen("derangement.in","r",stdin);freopen("derangement.out","w",stdout);scanf("%d",&n);fo(i,1,n) scanf("%d",&p[i]);f[0][0]=1,f[1][0]=0,f[0][1]=1,f[0][2]=2;fo(x,2,n) f[x][0]=(x-1)*(f[x-1][0]+f[x-2][0])%P;fo(x,1,n)fo(y,1,2)f[x][y]=(x*f[x-1][y]%P+y*f[x][y-1]%P)%P;ll s=0,ans=0;fo(i,2,n) s=(s+(i*(i-1)/2)%P)%P;fo(i,1,n)fo(j,i+1,n){ll a1,a2,a3;a1=max(0,p[j]-p[i]);a2=(p[j]*(p[j]-1)/2)%P;a2=(a2+((1+n-p[i])*(n-p[i])/2)%P)%P;a2=((a2-2*a1)%P+P)%P;a3=((s-a1-a2)%P+P)%P;a3=((a3-(p[i]*(p[i]-1)/2)%P)%P+P)%P;a3=((a3-((1+n-p[j])*(n-p[j])/2)%P)%P+P)%P;a3=a3+max(0,p[i]-p[j]);ans=(ans+(j-i)*(a1*f[n-2][0]%P+a2*f[n-3][1]%P+a3*f[n-4][2]%P)%P)%P;}printf("%d",ans);
}