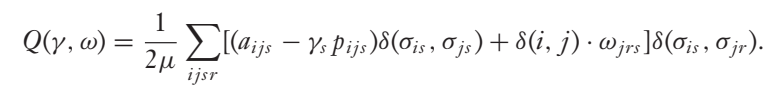modular专题
UVA - 10229 Modular Fibonacci
题意：矩阵快速幂取模 #include <iostream>#include <cstdio>#include <cstring>#include <cmath>using namespace std;long long mod;long long p[]={1,1,1,0};void matrix(long long a[],long long b[],long long c[]
pytest fixtures: explicit, modular, scalable 中文版
随着编程生涯的增长，会越来越发现，基本出现在中文相关资料的相关技术文章，靠谱的太少，老外的相反，真的是有种月亮还是外国的圆的感觉，最近想闲下来事情不多的时候，翻译一些，自己用到的，特别有用处的一些技术文章。前边的一篇JAVA NIO是第一篇，这将是第二篇。 python是一门特别容易上手，使用的语言，并且得益于其庞大的第三方库，使其具有其他脚本语言不具有的更多能力。或许这是众多软件使用pyth
【论文解读】Modular Blind Video Quality Assessment
原文下载地址：Modular Blind Video Quality Assessment 时间：2024 年 级别：arxiv 作者与机构：香港城市大学、香港中文大学（深圳）、字节跳动公司 git地址：https://github.com/winwinwenwen77/ModularBVQA 摘要 论文提出了一种模块化的盲视频质量评估（Blind Video Quality Assessm
Modular RPG Hero PBR
-掩码着色着色器提供了无限的颜色变化。（适用于标准/HDRP/URP 11.0.0） -为剑与盾/双剑/双剑姿态提供了简单的角色控制器。（不包括弓和魔杖控制器）（它是用旧的输入系统建造的） -HDRP/URP（11.0.0）SRP 100%支持常规着色器和遮罩着色着色器（基于着色器图形） -具有许多模块化部件和武器，可高度定制（有关详细信息，请查看屏幕截图） -针对手机游戏进行了优化（低多边形
ZOJ 3609 Modular Inverse
Description The modular modular multiplicative inverse of an integer a modulo m is an integer x such that a-1≡x (mod m). This is equivalent toax≡1 (mod m). Input There are multiple test case
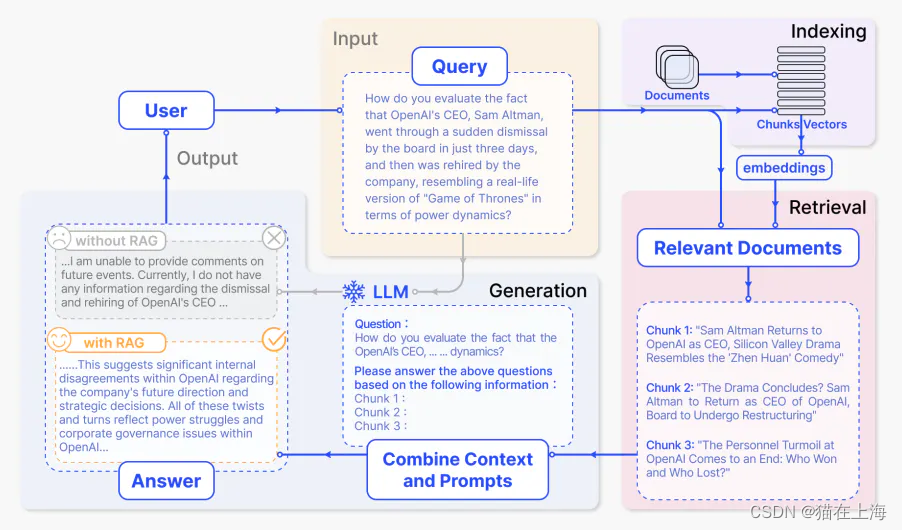
Naive RAG 、Advanced RAG 和 Modular RAG 简介
简介： RAG（Retrieval-Augmented Generation）系统是一种结合了检索（Retrieval）和生成（Generation）的机制，用于提高大型语言模型（LLMs）在特定任务上的表现。随着技术的发展，RAG系统经历了几个阶段的演变，包括Naive RAG、Advanced RAG和Modular RAG。 流程图 Naive RAG: Naive RAG是RA
快速幂取模运算(Modular Exponentiation)
不考虑取模的快速幂运算（迭代法） /* Iterative Function to calculate (x^y) in O(logy) */int power(int x, unsigned int y){int res = 1; // Initialize resultwhile (y > 0){// If y is odd, multiply x with resultif (
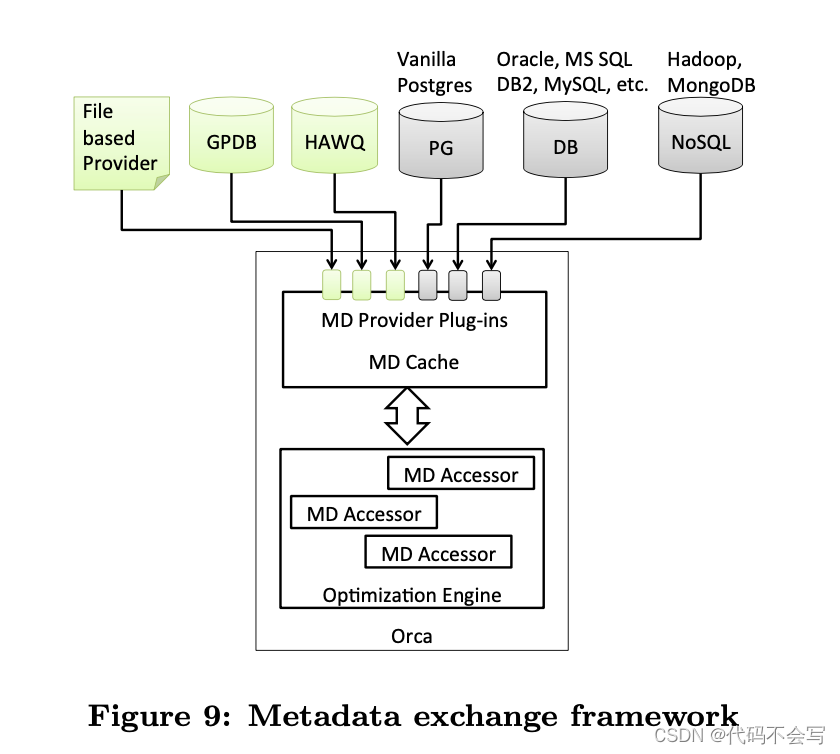
（论文阅读-优化器）Orca: A Modular Query Optimizer Architecture for Big Data
目录 摘要 一、简介 二、背景知识 2.1 大规模并行处理 2.2 SQL on Hadoop 三、Orca架构 四、查询优化 4.1 优化工作流 4.2 并行查询优化 五、Metadata Exchange 六、可行性 6.1 Minimal Repros 6.2 优化器准确性测试 七、实验 八、相关工作 8.1 查询优化基础 8.2 基于MPP数据库的SQ
Modular Multiplicative Inverse（模乘逆元）
计算模乘逆元原理上有四种方法： 1.暴力算法 2.扩展欧几里得算法 3.费尔马小定理 4.欧拉定理 模乘逆元定义：满足 ab≡1（mod m)，称b为a模乘逆元。以下是有关概念以及四种方法及程序。 文章出处：Modular Multiplicative Inverse The modular multiplicative inverse of an integer a modu
UVA10229 Modular Fibonacci 【循环数列】
The Fibonacci numbers (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...) are defined by the recurrence: F0 = 0 F1 = 1 Fi = Fi−1 + Fi−2 for i > 1 Write a program which calculates Mn = Fn mod 2^
Java 9 模块化(Modular)介绍
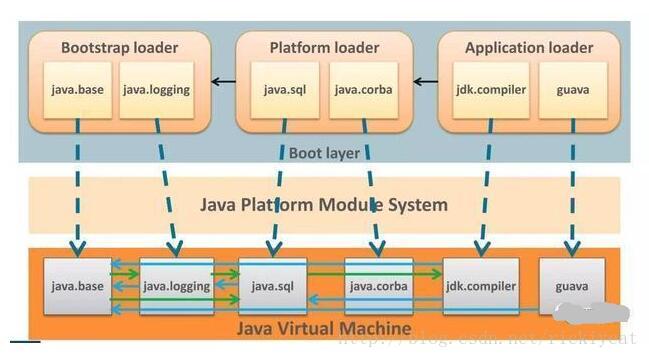
前言 今年，2017年，我们将迎来 Java 语言的 22 岁生日，22岁，对于一个人而言，正是开始大展鸿图的年纪，可是对于日新月异的科技圈中的一门开发语言而言，却是一个傲视群雄的老态龙钟的年纪。 JVM 语言发展史 JVM 家族也是在这22年中茁壮发展，并且都秉承着 Java 的革命口号：一处编译，随处运行。那么，JVM 的带头人 Java 在 9.0 的版本中带来了什么变化呢？
uva 10229 Modular Fibonacci
原题： The Fibonacci numbers (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …) are defined by the recurrence: F 0 = 0 F 1 =1 F i = F i−1 + F i−2 for i > 1 Write a program which calculates M n = F n mod 2 m f
[CryptoHack] MATHEMATICS-MODULAR MATH Write-Up
MATHEMATICS-MODULAR MATH目录 1. Quadratic Residues 2. Legendre Symbol 3. Modular Square Root 4. Chinese Remainder Theorem 1. Quadratic Residues 推荐视频 Quadratic Residues 即,a^2>p时, (a^2-x)是p的倍数
![[转载] Conv Nets: A Modular Perspective](http://colah.github.io/posts/2014-07-Conv-Nets-Modular/img/Conv2-5x5-Conv2-XY.png)
[转载] Conv Nets: A Modular Perspective
原文地址：http://colah.github.io/posts/2014-07-Conv-Nets-Modular/ Conv Nets: A Modular Perspective Posted on July 8, 2014 neural networks, deep learning, convolutional neural networks, modular neural ne
【博士每天一篇文献-综述】Modular Brain Networks
阅读时间：2023-11-27 1 介绍 年份：2016 作者：Olaf Sporns，Richard Betzel，印第安纳大学心理与脑科学杰出教授 期刊： Annual review of psychology 引用量：1205 详细介绍了模块化大脑网络及其如何利用图论工具进行分析，以检查大脑连接的结构和功能。首先介绍了大脑网络的概念以及检测这些网络中模块的方法。然后讨论了结构和功能大脑网
Codeforces Round 924 E. Modular Sequence
E. Modular Sequence 题意 对于一个长度为 n n n 的数组 a a a，定义它是 g o o d good good 的当且仅当： a 1 = x a_1 = x a1=x a i = a i − 1 + y a_{i} = a_{i - 1} + y ai=ai−1+y 或 a i = a i − 1 m o d y i ≥ 2 a_{i} = a
Leetcode 2961. Double Modular Exponentiation
Leetcode 2961. Double Modular Exponentiation 1. 解题思路2. 代码实现 题目链接：2961. Double Modular Exponentiation 1. 解题思路 这一题思路上没啥难的，主要就是实现上需要取一个巧。 显然当指数非常大的时候直接求pow的话答案会非常大，因此需要对其特殊处理一下，即使用二分的方式对计算量进行缩减，然后每次都
【刷题】Modular Multiplicative Inverse 模逆元
模逆元 定义 整数 a a a的模逆元是满足 a ⋅ x a\cdot x a⋅x模一个模数 m m m等于1。也就是找到一个数 x x x: a ⋅ x ≡ 1 mod m. a \cdot x \equiv 1 \text{ ~~~~mod m.} a⋅x≡1 mod m. 也可以把 x x x表示为 a − 1 a^{-1} a−1 需要注意模逆并不是总是存在。例如， m =
【MOJO】Modular语言安装和测试
目录 一、Mojo介绍 Linux Mac 二、安装Mojo SDK 三、mojo代码测试 3.1、在 REPL 中运行代码 3.2、构建并运行 Mojo 源文件 运行mojo文件 构建可执行二进制文件 四、VSCode安装 一、Mojo介绍 在学习Rust语言的过程中无意发现了Modular语言，语言的后缀为.mojo，这个语言通过调研还截止现在
有限域的Fast Multiplication和Modular Reduction算法实现
1. 引言 关于有限域的基础知识，可参考： RISC Zero团队2022年11月视频 Intro to Finite Fields: RISC Zero Study Club 有限域几乎是密码学中所有数学的基础。 ZKP证明系统中的所有运算都是基于有限域的： 使用布尔运算的数字电路：如AND、OR、NOT。使用有限域运算的算术电路：如addition、multiplication、ne
Java 9 模块化(Modular)介绍
前言 今年，2017年，我们将迎来 Java 语言的 22 岁生日，22岁，对于一个人而言，正是开始大展鸿图的年纪，可是对于日新月异的科技圈中的一门开发语言而言，却是一个傲视群雄的老态龙钟的年纪。 JVM 语言发展史 JVM 家族也是在这22年中茁壮发展，并且都秉承着 Java 的革命口号：一处编译，随处运行。那么，JVM 的带头人 Java 在 9.0 的版本中带来了什么变化呢？