logn专题
算法-搜索算法:二分查找(Binary Search)【前置条件:待查数据集必须是有序结构,可以右重复元素】【时间复杂度:O(logn)】
搜索:是在一个项目集合中找到一个特定项目的算法过程。搜索通常的答案是真的或假的,因为该项目是否存在。 搜索的几种常见方法:顺序/线性查找、二分法查找、二叉树查找、哈希查找 二分查找又称折半查找,优点是比较次数少,查找速度快,平均性能好;缺点是要求待查表: 必须采用顺序存储结构;必须按关键字大小有序排列;插入删除困难; 二分查找/折半查找方法适用于不经常变动而查找频繁的有序列表: 首先,假设
数据结构-高层数据结构:集合(Set)【元素不重复】【基于二分搜索树(有序集合O(logn))、基于平衡二叉树(有序集合O(logn))、基于链表(无序集合O(n))、基于哈希表(无序集合O(n))】
Set.java package set;/*** 集合** @author ronglexie* @version 2018/8/18*/public interface Set<E> {/*** 向集合中添加元素** @param e* @return void* @author ronglexie* @version 2018/8/18*/void add(E e);/*** 删
【算法题】找到任意一个峰值数字 要求时间复杂度为logn
在数组中找到一个峰值数字,其中峰值定义为比其相邻元素大的元素,可以使用二分查找算法来实现时间复杂度为O(log n)。 以下是一个Java示例,演示如何在一个整数数组中找到任意一个峰值数字: public class PeakFinder {public static int findPeakElement(int[] nums) {int left = 0, right = num
二分法的时间复杂度是logN
对数函数: (a>0, a≠1, x>0) 当α=e时,记为y=ln x 当α=10时,记为y=lg x 当α=2时,记为y=log x 其中x是自变量,函数的定义域是(0,+∞),即x>0。它实际上就是指数函数的反函数,可表示为x=a^y。 二分法的时间复杂度是logN 当有8个元素时,即x为8,y为3.
为什么堆排序的时间复杂度是O(N*logN)?
目录 前言: 堆排序(以排升序为例) 步骤(用大根堆,倒这排,排升序): 1.先把要排列的数组建立成大根堆 2.堆顶元素(82)和最后一个元素交换(2) 3.无视掉交换后的元素(82),对(2)进行向下调整 翻译成代码 mian方法: heapSortUp方法: siftDown方法: 堆排序时间复杂度分析: 前言: 本文章以升序为例进行讲解(实际上两
【算法基础】o(1), o(n), o(logn), o(nlogn)
由于平时接触算法比较少,今天看资料看到了o(1),都不知道是什么意思,百度之后才知道是什么意思。 描述算法复杂度时,常用o(1), o(n), o(logn), o(nlogn)表示对应算法的时间复杂度,是算法的时空复杂度的表示。不仅仅用于表示时间复杂度,也用于表示空间复杂度。 O后面的括号中有一个函数,指明某个算法的耗时/耗空间与数据增长量之间的关系。其中的n代表输入数据
斐波那契数列O(logn)的求解方法
前言 是的,没错,斐波那契数列除了递推、递归算法之外,还有更加高效的求解方法,那就是矩阵运算+快速幂。 思路: 可以先利用矩阵运算的性质将通项公式变成幂次形式,然后用平方倍增(快速幂)的方法求解第 n 项。 首先我们定义向量 Xn=[an an−1],边界:X1=[a1 a0] 然后我们可以找出矩阵: A = [ 1 1 1 0 ] A=\left[ \begin{matrix} 1
扩展区间的logn的方法(需要添加的最少的硬币数目)
这个题目的描述其实很简单,大致意思如下: 给你一个下标从 0 开始的整数数组 coins,表示可用的硬币的面值,以及一个整数 target 。 如果存在某个 coins 的子序列总和为 x,那么整数 x 就是一个 可取得的金额 。 返回需要添加到数组中的任意面值硬币的最小数量 ,使范围 [1, target] 内的每个整数都属于可取得的金额 。 数组的子序列是通过删除原始数组的一些(可能不删除)元
HDU 1025 Constructing Roads (最长上升子序列O(n*logn)算法)
题意: 多组输入,每组第一行输入N,接下来输入n组数据,每组数据两个数,第一个数代表poor city的下标p[i],第二个数代表rich city的下标r[i],意思是从r[i]到p[i]间建一条公路保证二者可以运输资源。但是每条公路都不能交叉,问最多能建几条公路。 解题思路: 常规DP来求最长上升子序列会TLE。这里Orz一种复杂度只有O(n*logn)的算法,自我感觉比线段树要好用
【58同城2017年笔试题】找到局部有序的数组的最小值,复杂度为O(logn)
题目: 对升序的排列的整数数组连续取前N个元素进行逆序排列,得到局部有序的数组,如: 【1,2,3,4,5,6】->【4,3,2,1,5,6】 假设数组元素无重复,从这种局部有序的数组中找到最小值,要求时间复杂度小于O(n),空间复杂度为O(1) 解题思路: ①找到数组的中间位置mid的值,将mid的左右两边的值进行比较; ②取mid和左右两边比较的小的一边,舍弃另一边; ③直到在限定范
一文读懂算法中的时间复杂度和空间复杂度,O(1)、O(logn)、O(n)、O(n^2)、O(2^n) 附举例说明,常见的时间复杂度,空间复杂度
时间复杂度和空间复杂度是什么 时间复杂度(Time Complexity)是描述算法运行时间长短的一个度量。空间复杂度(Space Complexity)是描述算法在运行过程中所需要的存储空间大小的一个度量。 时间复杂度和空间复杂度是衡量算法性能的重要指标。在实际开发中,我们通常会选择时间复杂度和空间复杂度都较低的算法。 时间复杂度可以用大O表示法来表示。大O表示法是用一个大写
认识O(N*logN)的排序(总结)
在总结之前看看下面这张表: 从表中可以看到归并排序、快速排序、堆排序的平均时间复杂度是 O(nlogn) 。我要总结的便是这三种排序算法,它们都适合于数据量比较大的排序运算中。 一. 归并排序: 归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。 首先考虑下如何将将二个有序数列合并。这个非常简单,只要从比较二
POJ2182 Lost Cows 树状数组 二分+树状数组(O(log^2n)/树状数组+倍增(O(logn))
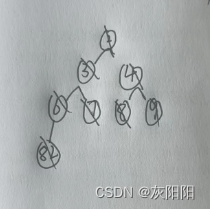
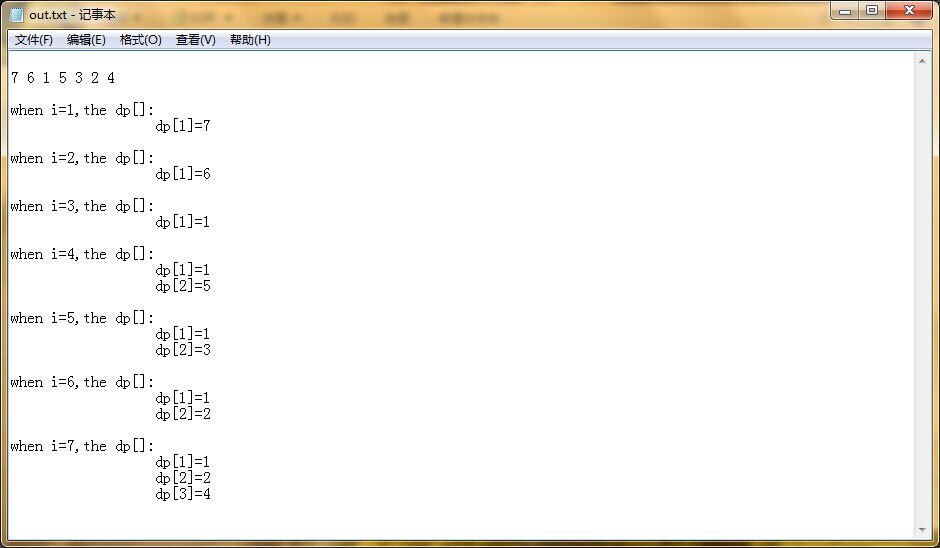
244. 谜一样的牛 题目 提交记录 讨论 题解 有n头奶牛,已知它们的身高为 1~n 且各不相同,但不知道每头奶牛的具体身高。 现在这n头奶牛站成一列,已知第i头牛前面有AiAi头牛比它低,求每头奶牛的身高。 输入格式 第1行:输入整数n。 第2..n行:每行输入一个整数AiAi,第i行表示第i头牛前面有AiAi头牛比它低。 (注意:因为第1头牛前面没有
logN的底数究竟是多少
问题: 关于算法的时间复杂度很多都用包含O(logN)这样的描述,但是却没有明确说logN的底数究竟是多少。 解答: 算法中log级别的时间复杂度都是由于使用了分治思想,这个底数直接由分治的复杂度决定。 如果采用二分法,那么就会以2为底数,三分法就会以3为底数,其他亦然。 不过无论底数是什么,log级别的渐进意义是一样的。 也就是说该算法的时间复杂度的增长与处理数据多少的增
算法学习—算法运行时间、logN、NlogN
1大部分程序的大部分指令之执行一次,或者最多几次。如果一个程序的所有指令都具有这样的性质,我们说这个程序的执行时间是常数。logN 如果一个程序的运行时间是对数级的,则随着N的增大程序会渐渐慢下来,如果一个程序将一个大的问题分解成一系列更小的问题,每一步都将问题的规模缩减成几分之一,一般就会出现这样的运行时间函数。在我们所关心的范围内,可以认为运行时间小于一个大的常数。对数的基数会影响这个常数,但