HDU 1025 Constructing Roads （最长上升子序列O（n*logn）算法）

本文主要是介绍HDU 1025 Constructing Roads （最长上升子序列O（n*logn）算法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题意：
多组输入，每组第一行输入N，接下来输入n组数据，每组数据两个数，第一个数代表poor city的下标p[i]，第二个数代表rich city的下标r[i]，意思是从r[i]到p[i]间建一条公路保证二者可以运输资源。但是每条公路都不能交叉，问最多能建几条公路。

解题思路：
常规DP来求最长上升子序列会TLE。这里Orz一种复杂度只有O（n*logn）的算法，自我感觉比线段树要好用的多，用到DP和二分知识。核心代码如下：

//dp[]数组是用来存所有长度为i的第i位的最小值。如果遇到长度为i的更小的值后面会一直更新。dp[]数组是一个升序序列，len为当前这个dp[]的长度。len的值最后就是最长上升子序列的长度。memset(dp,0,sizeof(dp));dp[0]=-1,dp[1]=r[1];int len = 1;for(int i=1;i<=n;i++) {int j=find(len,r[i]);//二分查找该数在dp[]中的位置dp[j]=r[i];//不管怎么样都要更新值if(j>len) len++;//如果j>len，说明又多了一位直接加上，如果j<=len,上面一步就已经更新了第j位的最小值}

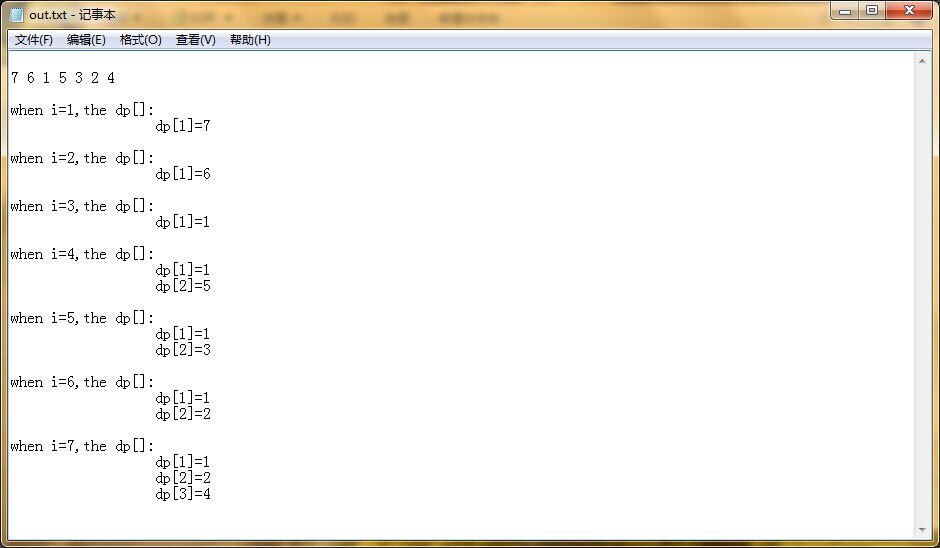
模拟一下就知道为什么了，如图所示，原序列数组为{7,6,1,5,3,2,4}
这里写图片描述

贴代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 500000+10;
int r[N],dp[N];
int find(int len,int x)
{int l=1,r=len;while(l<=r){int mid=(l+r)>>1;if(dp[mid]==x) return mid;else if(dp[mid]>x) r=mid-1;else l= mid+1;}return l;
}int main()
{int n,cas=1;while(~scanf("%d",&n)){int x,y;for(int i=1;i<=n;i++) scanf("%d%d",&x,&y),r[x]=y;memset(dp,0,sizeof(dp));dp[0]=-1,dp[1]=r[1];int len = 1;for(int i=1;i<=n;i++) {int j=find(len,r[i]);dp[j]=r[i];if(j>len) len++;}printf("Case %d:\n",cas++);if(len==1) printf("My king, at most 1 road can be built.\n");else printf("My king, at most %d roads can be built.\n",len);printf("\n");}return 0;
}