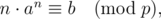equation专题
河南省第七届ACM【Turing equation】
【Description】 The fight goes on,whether to store numbers starting withtheir most significant digit or their least significant digit. Sometimes this isalso called the "Endian War". The battlegro
SGU 106. The equation 扩展欧几里德
求解的个数 对应ax+by=c 根据裴蜀定理c%gcd(a, b) == 0有解 假设d = gcd(a, b) 用扩展欧几里德求出方程aax+bb*y=cc 的解x0 y0 那么原方程的一个解就是x0*c/d和y0*c/d 通解为 x = x0+i*b/d y = y0+i*a/d 分别讲x1 x2 带入得到i 满足最小的左区间 y1 y2一样 #include <cstd
SGU106 The equation
<span style="font-family: Arial, Helvetica, sans-serif; background-color: rgb(255, 255, 255);"><span style="font-size:14px;">题意:给出直线ax+by+c=0的参数a, b, c,求直线在 x ∈[x1, x2],y ∈[y1, y2] 上有多少整点。</span></s
里卡提方程(Riccati Equation)例子
里卡提方程(Riccati Equation) 里卡提方程(Riccati Equation)在人形机器人控制中有重要的应用,特别是在最优控制和估计问题中。里卡提方程主要用于求解线性二次型调节器(LQR, Linear Quadratic Regulator)和卡尔曼滤波器(Kalman Filter)。这些方法有助于提高机器人控制的稳定性和性能。 里卡提方程简介 离散时间里卡提方程的一般形
fzu 2102 Solve equation(水题)
题目连接:fzu 2102 Solve equation 题目大意:给出数a,b和进制bas,a和b都是bas进制的数,现在要计算十进制数k和d ,使得a = k * b + d。 解题思路:将a和b转换成十进制数,然后k = a / b, d =a - (a/b) * b. #include <stdio.h>#include <string.h>const int
SGU 106 The equation(拓展欧几里得)
通解形式 然后利用x,y去求出范围,就能得到解的个数 注意特判a和b都为0的情况 代码: #include <cstdio>#include <cstring>#include <cmath>#include <algorithm>using namespace std;typedef long long ll;ll a, b, c;double a1, a2, b1
HDU 2199 Can you solve this equation? NYOJ 503 解方程
题目链接~~> 做题感悟:这个题太坑(也许暗示着对二分还没掌握好),调精度调了半上午才调出来。 解题思路:在[ 0 , 100 ] 这个区间里函数是单调递增的所以与二分有一点的差别(个人感觉),只要在 F( 0 ) ~ F( 100 ) 之间的值都有解不断二分即可,也不用加 0.000001 ,其实加也可以. 总结一下 pow ( x , y ) :
Twice Equation(递推+java大数)
问题 L: Twice Equation 题目描述 For given L, find the smallest n no smaller than L for which there exists an positive integer m for which 2m(m + 1) = n(n + 1). 输入 This problem contains multiple
【RL】Bellman Equation (贝尔曼等式)
Lecture2: Bellman Equation State value 考虑grid-world的单步过程: S t → A t R t + 1 , S t + 1 S_t \xrightarrow[]{A_t} R_{t + 1}, S_{t + 1} StAt Rt+1,St+1 t t t, t + 1 t + 1 t+1:时间戳 S t S_t St:时间
quadratic equation (余数)
quadratic equation Time Limit: 2000 ms Memory Limit: 131072 KiB Submit Statistic Discuss Problem Description With given integers a,b,c, you are asked to judge whether the following statem
Quaternion Screened Poisson Equation for Low-Light Image Enhancement——论文笔记
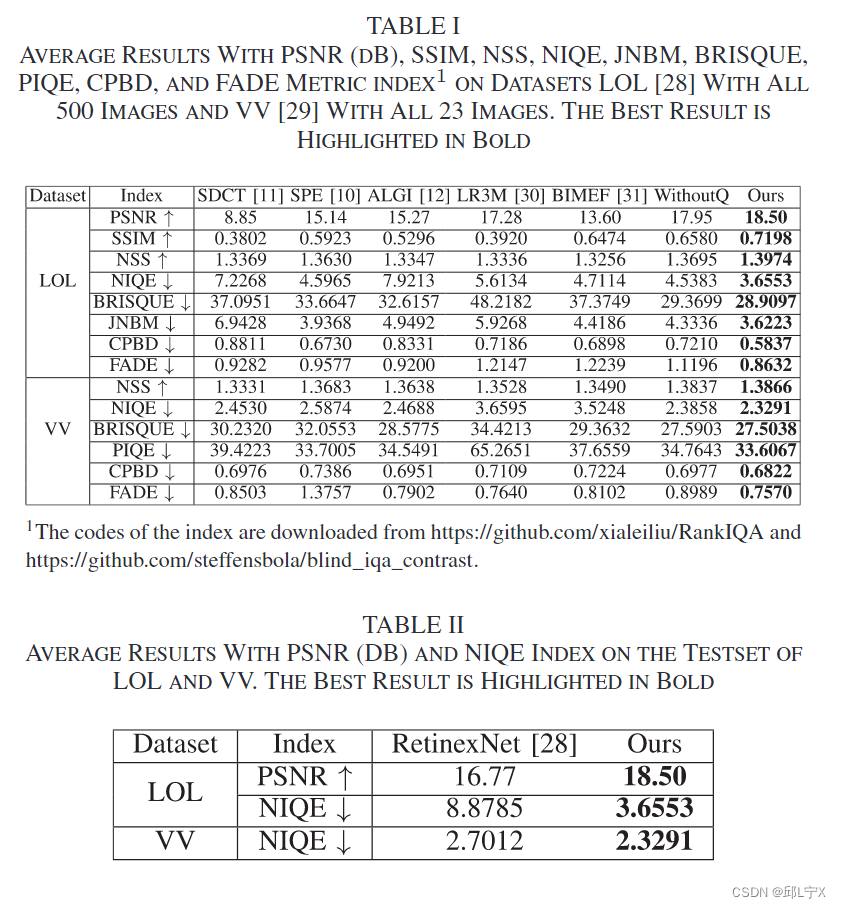
摘要: 图像增强是一种增强低照度图片照度的方法,它能在增强的同时保持图像的真实度和自然度。对于彩色图像,大多数方法采用分开处理不同彩色通道的方式,但这样会忽略掉不同彩色通道间的联系。因此,本文采用基于四元数(Quaternion)的模型去保留颜色相关性,它可以通过四元数将某一像素的颜色信息整合起来。此外,我们提出了基于伽马校正函数(Gamma-correction functio
算法提高 ADV-111 Quadratic Equation
问题描述 求解方程ax 2+bx+c=0的根。要求a, b, c由用户输入,并且可以为任意实数。 输入格式:输入只有一行,包括三个系数,之间用空格格开。 输出格式:输出只有一行,包括两个根,大根在前,小根在后,无需考虑特殊情况,保留小数点后两位。 输入输出样例 样例输入 2.5 7.5 1.0 样例输出 -0.14 -2.86
ACM 第八届山东省赛 F quadratic equation SDUT 3898
再次提交链接: 点击打开链接 quadratic equation Time Limit: 2000MS Memory Limit: 131072KB Submit Statistic Problem Description With given integers a,b,c, you are asked to judge whether the f
机器学习第二周--Multiple features Normal equation
多变量的线性回归 多变量特征缩放均值归一化学习速率多项式回归 常规方程常规方程和梯度下降比较 多变量的线性回归 第一周内容针对单变量,也就是一个feature。这此考虑多变量,即多个features。 仍然与预测房价为例,影响房价的因素不只有面积,我们加入卧室数量、楼层、房龄,这些可看作新加入的feature。由此我们有以下表示: m是样本数目,n是特征数目,X的上标
强化学习-赵世钰(二):贝尔曼公式/Bellman Equation【用于计算State Value:①线性方程组法、②迭代法】、Action Value【据状态值求解得到;用来评价action优劣】
State Value :the average Return that an agent can obtain if it follows a given policy/π【给定一个policy/π,所有可能的trajectorys得到的所有return的平均值/期望值: v π ( s ) ≐ E [ G t ∣ S t = s ] v_\pi(s)\doteq\mathbb{E}[G_t|
xctf攻防世界 CRYPTO高手进阶区 equation-2
0x01. 进入环境,下载附件 题目给的两个文件,一个enc加密文件,一个是一张图片,如图: 0x02. 问题分析 0x02_1. 对应字段 我们可以看到,整个私钥的上半段被加密了,只给了后半段。看到这里,我们首先必须了解私钥文件pem的结构类型,参考链接:http://blog.sina.com.cn/s/blog_4fcd1ea30100yh4s.html。如图: 其次,我们将图
【学习Reynolds Equation】
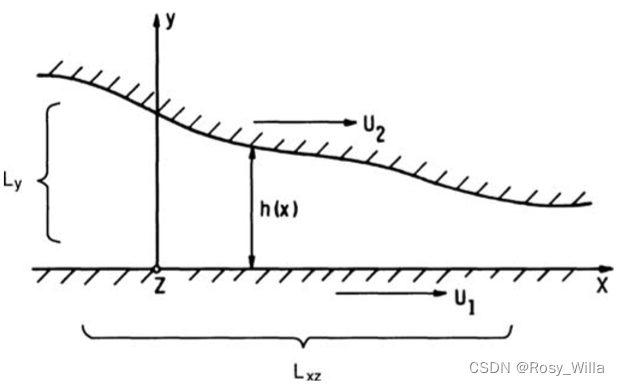
学习Reynolds Equation Reynolds Equation的定义Reynolds Equation 表达式Average Reynolds Equation最终Average Reynolds Equation Reynolds Number雷诺数Reynolds Equation 的推导Reynolds Equation 的解Reynolds Equation的推导
BUUCTF--equation
测试文件:https://www.lanzous.com/ib50p4f 代码分析 在题目中已经提到了对代码进行Fuck混淆,因此对于if中的代码,我们只需要解码,让flag满足要求即可。 第一种解法 http://codertab.com/JsUnFuck 可以到这个网站,将混淆的代码一部分一部分的解,不过过程很繁琐... 第二种解法 使用脚本解码 <script>func
0051【Edabit ★☆☆☆☆☆】【解析表达式】Solve the Equation
0051【Edabit ★☆☆☆☆☆】【解析表达式】Solve the Equation language_fundamentals math Instructions Create a function that takes an equation (e.g. "1+1"), and returns the answer. Examples equation("1+1") //
Codeforces 919 E Congruence Equation
题目描述 Given an integer xx . Your task is to find out how many positive integers nn ( 1<=n<=x1<=n<=x ) satisfy where a,b,pa,b,p are all known constants. 输入输出格式 输入格式: The only line contains four inte
Codeforces Round #460 (Div. 2) E. Congruence Equation 数学
E. Congruence Equation solution { i ∗ a i % p = b , i < p − 1 , ( t − k ) ∗ a t % p = b , i ≥ p − 1 , i = ( p − 1 ) k + t . \begin{cases} i*a^i\%p=b,i<p-1, \\(t-k)*a^{t}\%p=b,i≥p-1,i=(p-1)k+t. \e
泛函分析(二)巴纳赫(Banach)不动点,贝尔曼方程(Bellman equation)在强化学习的应用
前言 强化学习的目的是寻找最优策略。其中涉及两个核心概念最优状态值和最优策略,以及贝尔曼最优公式。而贝尔曼最优公式用不动点原理求解地址,由Banach不动点定理可以知道,强化学习一定存在唯一的解(策略) ,并且可以通过迭代求得。 1.贝尔曼方程 贝尔曼方程在强化学习(RL)中无处不在,由美国应用数学家理查德·贝尔曼(Richard Bellman)提