本文主要是介绍【学习Reynolds Equation】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
学习Reynolds Equation
- Reynolds Equation的定义
- Reynolds Equation 表达式
- Average Reynolds Equation
- 最终Average Reynolds Equation
- Reynolds Number雷诺数
- Reynolds Equation 的推导
- Reynolds Equation 的解
- Reynolds Equation的推导
大家好!该篇博文是根据链接: Reynolds Equation – An Overview.https://www.tribonet.org/wiki/reynolds-equation/学习内容的笔记。Willa把一些要点进行了摘录,有不对的,望大家指正,谢谢哦!
需要大家注意的是,文中提到Reynolds方程仍然很复杂,很多润滑问题尚需要研究。
Reynolds Equation的定义
Reynolds Equation源于Navier-Stokes Equation,是经典润滑理论的基本方程之一。流体动力学和弹性流体动力学润滑理论最实际应用的基础。
本质是一个偏微分方程,用于描述两个表面之间薄润滑膜的流动。
Prefessor Osborne Reynolds在轴承摩擦的实验中,他发现流体动力压力在接触中心后,快速达到了峰值。Reynolds 认为润滑剂被“拖”到接触点中,形成了一层承载施加在物体上的负载薄膜。Reynolds教授的主要成就是将Navier-Stokes Equation方程(包括润滑剂的惯性和粘度的影响)简化为一种可以通过解析求解的形式(这在当时是唯一可能的方法),并且仍然很好地描述了润滑剂的流动。
Reynolds Equation 表达式
参考雷诺方程https://baike.sogou.com/v57080390.htm由英国物理学家Osborne Reynolds于1886年提出。
∂ ∂ x ( p h 3 12 μ ∂ p ∂ x ) + ∂ ∂ y ( p h 3 12 μ ∂ p ∂ y ) = ∂ ∂ x ( p h ( u a + u b ) 2 ) + ∂ ∂ y ( p h ( u a + u b ) 2 ) + ρ ( w a − w b ) − ρ u a ∂ h ∂ x − ρ u a ∂ h ∂ y + h ∂ ρ ∂ t (1) \frac{\partial }{\partial x}(\frac{ph^3}{12\mu}\frac{\partial p}{\partial x})+\frac{\partial }{\partial y}(\frac{ph^3}{12\mu}\frac{\partial p}{\partial y})=\frac{\partial}{\partial x}(\frac{ph(u_a+u_b)}{2})+\frac{\partial}{\partial y}(\frac{ph(u_a+u_b)}{2})+\rho(w_a-w_b)-\rho u_a\frac{\partial h}{\partial x}-\rho u_a\frac{\partial h}{\partial y}+h\frac{\partial \rho}{\partial t}\tag{1} ∂x∂(12μph3∂x∂p)+∂y∂(12μph3∂y∂p)=∂x∂(2ph(ua+ub))+∂y∂(2ph(ua+ub))+ρ(wa−wb)−ρua∂x∂h−ρua∂y∂h+h∂t∂ρ(1)
其中,
p 为流体膜压力 p为流体膜压力 p为流体膜压力
x 为流体轴承宽度方向的坐标 x为流体轴承宽度方向的坐标 x为流体轴承宽度方向的坐标
y 为流体轴承长度方向的坐标 y为流体轴承长度方向的坐标 y为流体轴承长度方向的坐标
z 为流体膜厚度方向的坐标 z为流体膜厚度方向的坐标 z为流体膜厚度方向的坐标
h 为流体膜厚度 h为流体膜厚度 h为流体膜厚度
μ 为流体黏度 \mu为流体黏度 μ为流体黏度
ρ 为流体密度 \rho为流体密度 ρ为流体密度
u , v , w 分别为 x , y , z 方向的边界速度 u,v,w分别为x,y,z方向的边界速度 u,v,w分别为x,y,z方向的边界速度
a 为上边界 a为上边界 a为上边界
b 为下边界 b为下边界 b为下边界
Average Reynolds Equation
对于等温、不可压缩的润滑,流体弹性动力学压力由Reynolds方程控制,得到An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication:
∂ ∂ x ( h T 3 12 μ ∂ p ∂ x + ∂ ∂ x ( h T 3 12 μ ∂ p ∂ y ) = U 1 + U 2 2 ∂ h T ∂ x + ∂ h T ∂ y (2) \frac{\partial }{\partial x}(\frac{h_{T^3}}{12\mu}\frac{\partial p}{\partial x}+\frac{\partial }{\partial x}(\frac{h_{T^3}}{12\mu}\frac{\partial p}{\partial y})=\frac{U_1+U_2}{2}\frac{\partial h_T}{\partial x}+\frac{\partial h_T}{\partial y}\tag{2} ∂x∂(12μhT3∂x∂p+∂x∂(12μhT3∂y∂p)=2U1+U2∂x∂hT+∂y∂hT(2)
其中, h T h_T hT为局部膜厚; U 1 和 U 2 U_1和U_2 U1和U2是齿轮表面x方向的齿面速度。
q x = − h T 3 12 μ ∂ p ∂ x + U 1 + U 2 2 h T ( 3 ) (3) q_x=-\frac{h_{T^3}}{12\mu}\frac{\partial p}{\partial x}+\frac{U_1+U_2}{2}h_T (3)\tag{3} qx=−12μhT3∂x∂p+2U1+U2hT(3)(3)
q y = − h T 3 12 μ ∂ p ∂ y (4) q_y=-\frac{h_{T^3}}{12\mu}\frac{\partial p}{\partial y} \tag{4} qy=−12μhT3∂y∂p(4)
q ‾ x = 1 Δ y ∫ y y + Δ y q x d y = 1 Δ y ∫ y y + Δ y ( − h T 3 12 μ ∂ p ∂ x + U 1 + U 2 2 h T ) d y = − ϕ x h 3 12 μ ∂ p ‾ ∂ x + U 1 + U 2 2 h ‾ T + U 1 − U 2 2 σ ϕ s (5) \overline{q}_x =\frac{1}{\Delta y}\int_{y}^{y+\Delta y}q_xdy =\frac{1}{\Delta y}\int_{y}^{y+\Delta y}(-\frac{h_{T^3}}{12\mu}\frac{\partial p}{\partial x}+\frac{U_1+U_2}{2}h_T)dy\\=-\phi_x\frac{h^3}{12\mu}\frac{\partial \overline{p}}{\partial x}+\frac{U_1+U_2}{2}\overline{h}_T+\frac{U_1-U_2}{2}\sigma\phi_s\tag{5} qx=Δy1∫yy+Δyqxdy=Δy1∫yy+Δy(−12μhT3∂x∂p+2U1+U2hT)dy=−ϕx12μh3∂x∂p+2U1+U2hT+2U1−U2σϕs(5)
q ‾ y = 1 Δ x ∫ x x + Δ x q y d x = 1 Δ x ∫ x x + Δ x ( − h T 3 12 μ ∂ p ∂ y ) d x = − ϕ y h 3 12 μ ∂ p ‾ ∂ y (6) \overline{q}_y=\frac{1}{\Delta x}\int_{x}^{x+\Delta x}q_ydx=\frac{1}{\Delta x}\int_{x}^{x+\Delta x}(-\frac{h_{T^3}}{12\mu}\frac{\partial p}{\partial y})dx=-\phi_y\frac{h^3}{12\mu}\frac{\partial \overline{p}}{\partial y}\tag{6} qy=Δx1∫xx+Δxqydx=Δx1∫xx+Δx(−12μhT3∂y∂p)dx=−ϕy12μh3∂y∂p(6)
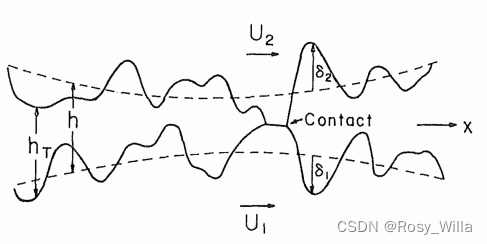
其中, h h h为标称膜厚; q x 和 q y q_x和q_y qx和qy分别为在x,y方向的单位油流体; q ‾ x 和 q ‾ y \overline{q}_x和\overline{q}_y qx和qy分别为单位油流体的均值; σ = σ 1 2 + σ 2 2 \sigma=\sqrt{\sigma_1^2+\sigma_2^2} σ=σ12+σ22为 σ 1 和 σ 2 \sigma_1和\sigma_2 σ1和σ2的总粗糙度的标准差, σ 1 和 σ 2 \sigma_1和\sigma_2 σ1和σ2分别为粗糙度 δ 1 和 δ 2 \delta_1和\delta_2 δ1和δ2的标准差; ϕ x 和 ϕ y \phi_x和\phi_y ϕx和ϕy为流因子; ϕ s \phi_s ϕs为剪切流因子。
最终Average Reynolds Equation
∂ ∂ x ( ϕ x h 3 12 μ ∂ p ‾ ∂ x ) + ∂ ∂ y ( ϕ y h 3 12 μ ∂ p ‾ ∂ y ) = U 1 + U 2 2 ∂ h ‾ T ∂ x + U 1 − U 2 2 σ ∂ ϕ s ∂ x + ∂ h ‾ T ∂ t (7) \frac{\partial}{\partial x}(\phi_x\frac{h^3}{12\mu}\frac{\partial \overline{p}}{\partial x})+\frac{\partial}{\partial y}(\phi_y\frac{h^3}{12\mu}\frac{\partial \overline{p}}{\partial y})=\frac{U_{1}+U_{2}}{2}\frac{\partial \overline{h}_T}{\partial x}+\frac{U_{1}-U_{2}}{2}\sigma\frac{\partial \phi_s}{\partial x}+\frac{\partial \overline{h}_T}{\partial t}\tag{7} ∂x∂(ϕx12μh3∂x∂p)+∂y∂(ϕy12μh3∂y∂p)=2U1+U2∂x∂hT+2U1−U2σ∂x∂ϕs+∂t∂hT(7)
Reynolds Number雷诺数
雷诺数 R e Re Re是一个无量纲数。其公式为: R e = 惯性力 粘性力 = ρ u h μ (8) Re=\frac{惯性力}{粘性力}=\frac{\rho u h}{\mu}\tag{8} Re=粘性力惯性力=μρuh(8)其中, ρ \rho ρ是密度(单位: k g / m 3 kg/m^3 kg/m3), u u u是特征速度(单位: m / s m/s m/s), h h h是特征长度(单位: m m m;在流体动力学润滑理论中通常指中心膜厚度), μ \mu μ是流体粘度(单位: P a ⋅ s Pa·s Pa⋅s)用于描述流体层留到湍流的转变,是一个重要参数。
Reynolds Equation 的推导
观察中:润滑剂被视为等粘性和流层,流体膜的曲率忽略不计。
假设:
1.粘度恒定,牛顿润滑剂,流体为牛顿流体
2.薄膜几何形状,流体膜厚度远远小于宽度与长度 ( h < < l 及 h < < w ) (h<<l及h<<w) (h<<l及h<<w)
3.体积力可忽略,黏性力大于惯性力(雷诺数很小)
4.无滑移边界条件,压力沿厚度方向基本不变 ∂ p ∂ z = 0 \frac{\partial p}{\partial z}=0 ∂z∂p=0
以下图片来自于链接: link
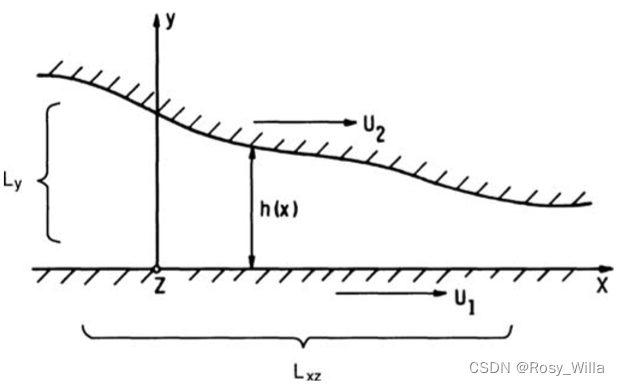
根据连接https://books.google.nl/books/about/Fluid_Film_Lubrication.html?id=U5VXXRAgKwsC&redir_esc=y
得到以下公式
∂ p ∂ x = μ ∂ 2 u ∂ y 2 (9) \frac{\partial p}{\partial x}=\mu\frac{\partial^2u}{\partial y^2}\tag{9} ∂x∂p=μ∂y2∂2u(9) ∂ p ∂ z = μ ∂ 2 w ∂ y 2 (10) \frac{\partial p}{\partial z}=\mu\frac{\partial^2w}{\partial y^2}\tag{10} ∂z∂p=μ∂y2∂2w(10) ∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0 (11) \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0\tag{11} ∂x∂u+∂y∂v+∂z∂w=0(11)
文中提到假设润滑剂不可压缩。
薄膜几何形状
u = 1 2 u ∂ p ∂ x y 2 + A y + B (12) u=\frac{1}{2u}\frac{\partial p}{\partial x}y^2+Ay+B\tag{12} u=2u1∂x∂py2+Ay+B(12)
w = 1 2 u ∂ p ∂ z y 2 + C y + D (13) w=\frac{1}{2u}\frac{\partial p}{\partial z}y^2+Cy+D\tag{13} w=2u1∂z∂py2+Cy+D(13)
边界条件
u = U 1 , w = 0 , y = 0 (14) u=U_{1},w=0,y=0\tag{14} u=U1,w=0,y=0(14)
u = U 2 , w = 0 , y = h (15) u=U_{2},w=0,y=h\tag{15} u=U2,w=0,y=h(15)
其中, U 1 U_{1} U1和 U 2 U_{2} U2表示轴承表面的速度。
速度分布(通过积分得到)
u = 1 2 μ ∂ p ∂ x ( y 2 + y h ) + ( 1 − y h ) U 1 + y h U 2 (16) u=\frac{1}{2\mu}\frac{\partial p}{\partial x}(y^2+yh)+(1-\frac{y}{h})U_{1}+\frac{y}{h}U_{2}\tag{16} u=2μ1∂x∂p(y2+yh)+(1−hy)U1+hyU2(16) w = 1 2 μ ∂ p ∂ z ( y 2 − y h ) (17) w=\frac{1}{2\mu}\frac{\partial p}{\partial z}(y^2-yh)\tag{17} w=2μ1∂z∂p(y2−yh)(17)
根据连续性:
∫ 0 h − ∂ v ∂ y d y = ∫ 0 h ∂ u ∂ x d y + ∫ 0 h ∂ w ∂ z d y (18) \int_0^{h}-\frac{\partial v}{\partial y} \mathrm{d}y=\int_0^{h}\frac{\partial u}{\partial x} \mathrm{d}y+\int_0^{h}\frac{\partial w}{\partial z} \mathrm{d}y\tag{18} ∫0h−∂y∂vdy=∫0h∂x∂udy+∫0h∂z∂wdy(18)
根据Reynolds润滑压力方程进行积分:
∂ ∂ x ( h 3 μ ∂ p ∂ x ) + ∂ ∂ z ( h 3 μ ∂ p ∂ z ) = 6 ( U 1 + U 2 ) ∂ h ∂ x + 12 ∂ h ∂ t (19) \frac{\partial}{\partial x}(\frac{h^3}{\mu}\frac{\partial p}{\partial x})+ \frac{\partial}{\partial z}(\frac{h^3}{\mu}\frac{\partial p}{\partial z})=6(U_{1}+U_{2})\frac{\partial h}{\partial x}+12\frac{\partial h}{\partial t}\tag{19} ∂x∂(μh3∂x∂p)+∂z∂(μh3∂z∂p)=6(U1+U2)∂x∂h+12∂t∂h(19)
详细推导过程可以根据连接
Reynolds Equation 的解
通常,Reynolds Equation在基于边界条件和考虑的几何形状以及某些假设情况下,采用有限差分或有限元等数值方法可进行求解得到解析。
文中提到的相关的代码可以在连接中找到。
Reynolds Equation的推导
根据以上公式等推导出了各种广义雷诺方程,以削弱用于推导经典形式的假设。例如,可以考虑可压缩的非牛顿润滑剂行为。在摩擦学中,雷诺方程用于预测润滑膜的厚度,也用于预测润滑剂在表面上产生的摩擦。由于许多摩擦学触点在高负载状态和薄膜中工作,因此剪切速率可能非常高(大约 107-109 )。许多典型的润滑剂在接触条件下开始表现为非牛顿润滑剂,因此,雷诺方程被推广到非牛顿润滑剂的情况。另一个推广包括滑移边界条件。这种形式的雷诺方程用于计算纹理表面或高滑移表面的薄膜厚度和摩擦力。
参考文献:
[1]https://www.tribonet.org/wiki/reynolds-equation/
[2]https://baike.sogou.com/v57080390.htm
[3]https://baike.sogou.com/v8658439.htm
[4]An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication:
这篇关于【学习Reynolds Equation】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









