题目描述
Given an integer xx . Your task is to find out how many positive integers nn ( 1<=n<=x1<=n<=x ) satisfy
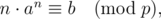where a,b,pa,b,p are all known constants.
输入输出格式
输入格式：
The only line contains four integers a,b,p,xa,b,p,x ( 2<=p<=10^{6}+32<=p<=106+3 , 1<=a,b<p1<=a,b<p , 1<=x<=10^{12}1<=x<=1012 ). It is guaranteed that pp is a prime.
输出格式：
Print a single integer: the number of possible answers nn .
输入输出样例
输入样例#1：
2 3 5 8
输出样例#1：
2
输入样例#2：
4 6 7 13
输出样例#2：
1
输入样例#3：
233 233 10007 1
输出样例#3：
1
说明
In the first sample, we can see that n=2n=2 and n=8n=8 are possible answers.
利用同余乱搞即可，系数是mod p的同余系，指数是mod (p-1)的同余系。
不过写之前一定要想好，不然特别容易写错(细节略多)。。。
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define ll long long
#define maxn 1000010
using namespace std;
ll ans,inv[maxn],b,d;
ll ci[maxn],p,tp;inline void init(const ll ha){ci[0]=1;for(int i=1;i<ha;i++) ci[i]=ci[i-1]*d%ha;inv[1]=1;for(int i=2;i<ha;i++) inv[i]=-inv[ha%i]*(ha/i)%ha+ha;
}inline void solve(const ll ha){ll tmpc,tmpd;ll basec=(tp+1)/(ha-1),lefc=tp+1-basec*(ha-1);//basec表示指数上有多少个完整的循环节//lefc表示最后多出来的可以走的步数 for(int i=p-2;i>=0;i--){int to=b*inv[ci[i]]%ha;tmpc=basec+(i<lefc);//tmpc是计算a^i这个数出现的次数 tmpd=tmpc/ha+((i-to+ha)%ha<tmpc%ha);//因为每次指数对应的系数都会-1，//所以就相当于计算在系数的同余系下//从i开始倒退走tmp-1步能走到to多少次 ans+=tmpd;}
}int main(){scanf("%lld%lld%lld%lld",&d,&b,&p,&tp);init(p);solve(p);printf("%lld\n",ans);return 0;
}
