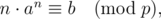分析 关键是这句话的转化 每行的任意两个数（相同j）的差不相等 那么我们有一个想法就是，每行有一个固定的diff diff从0取到n - 1 这个显然是对的 每行相同的j1, j2差都不一样 设为diff = 0, 1 ,…, n - 1 设gap = j2 - j1 (d2 - d1) * gap != 0 (mod n) n为质数, gap in [1, n - 1], (d2 - d1

题目链接 题解： 这道题，看起来既要平移又要旋转，挺麻烦。可以抓住一个性质，如果这两个点集可以通过旋转匹配，那么，这两个点集中的点相对重心的位置分布是相同的。 因此，我们可以先求出这两个点集中的点相对其重心的相对坐标，这样我们就能够忽略掉平移这个操作所带来的影响。 下面就要考虑能否通过旋转使两个点集匹配。 从点集 S S S中选一个 x x x坐标不为0的点 p p p，这样可以保证有

https://en.wikipedia.org/wiki/Congruence_relation   https://zh.wikipedia.org/wiki/%E5%90%8C%E9%A4%98%E9%97%9C%E4%BF%82   在数学特别是抽象代数中，同余关系或简称同余是相容于某个代数运算的等价关系。 目录 1 模算术2 线性代数3 泛代数4 群的同余、正规子群和理想

题目描述 Given an integer xx . Your task is to find out how many positive integers nn ( 1<=n<=x1<=n<=x ) satisfy  where a,b,pa,b,p are all known constants. 输入输出格式 输入格式：   The only line contains four inte

E. Congruence Equation solution { i ∗ a i % p = b ， i < p − 1 , ( t − k ) ∗ a t % p = b ， i ≥ p − 1 ， i = ( p − 1 ) k + t . \begin{cases} i*a^i\%p=b，i<p-1, \\(t-k)*a^{t}\%p=b，i≥p-1，i=(p-1)k+t. \e