divergence专题
KL散度(Kullback-Leibler divergence)
K L KL KL散度( K u l l b a c k − L e i b l e r d i v e r g e n c e Kullback-Leibler\ divergence Kullback−Leibler divergence),也被称为相对熵、互熵或鉴别信息,是用来衡量两个概率分布之间的差异性的度量方法。以下是对 K L KL KL散度的详细解释: 定义 K L KL
KL divergence(KL 散度)详解
本文用一种浅显易懂的方式说明KL散度。 参考资料 KL散度本质上是比较两个分布的相似程度。 现在给出2个简单的离散分布,称为分布1和分布2. 分布1有3个样本, 其中A的概率为50%, B的概率为40%,C的概率为10% 分布2也有3个样本: 其中A的概率为50%,B的概率为10%,C的概率为40%。 现在想比较分布1和分布2的相似程度。 直观看上去分布1和分布2中样本A的概率是一样的
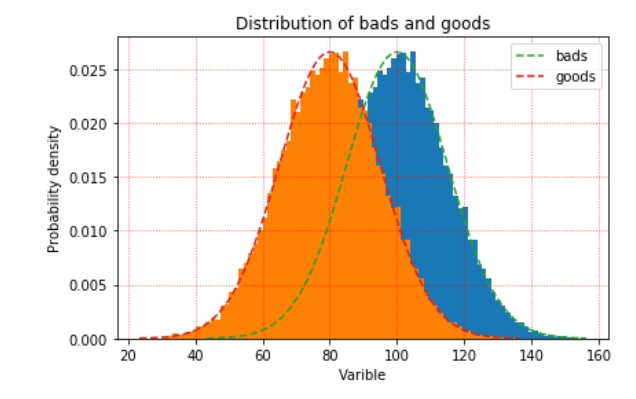
智能风控体系之divergence评分卡简介
评分卡模型的出现据说最早是在20世纪40年代,Household Finance and Spiegel和芝加哥邮购公司第一次尝试在贷款决策过程中使用信用评分.但是这两家公司都终止了这项业务。后来,在20世纪50年代末,伊利诺伊州的美国投资公司(AIC)聘请两位数学家比尔·法尔(Bill Fair)和厄尔·艾萨克 (Earl Isaac)通过审查一个小型贷款样本(其中一些支付信用良好,其中一些较差
Pinsker’s inequality 与 Kullback-Leibler (KL) divergence / KL散度
文章目录 Pinsker’s inequalityKullback-Leibler (KL) divergenceKL散度在matlab中的计算 KL散度在隐蔽通信概率推导中的应用 Pinsker’s inequality Pinsker’s Inequality是信息论中的一个不等式,通常用于量化两个概率分布之间的差异。这个不等式是由苏联数学家Mark Pinsker于1964
Kullback-Leibler Divergence(KL散度)
下面一篇文章在例子中直观通俗理解KL散度: Kullback-Leibler Divergence Explained Light on Math Machine Learning: Intuitive Guide to Understanding KL 上文中文翻译链接:https://www.sohu.com/a/233776078_164987 知乎回答:https://www
KL散度 kl divergence
KL散度也叫KL距离 也叫相对熵 relative entropy。是描述两个概率分布P和Q差异的一种方法。它是非对称的,这意味着D(P||Q) ≠ D(Q||P)。特别的,在信息论中,D(P||Q)表示当用概率分布Q来拟合真实分布P时,产生的信息损耗,其中P表示真实分布,Q表示P的拟合分布。 离散随机变量的两个概率分布P、Q的KL散度定义为: 连续随机变量P,Q的KL散度定义为:
KL divergence
真正的概率分布: A0 = 1/2,A1= 1/2 模型1:b1 = 1/4, b2 = 3/4 模型2: c1 = 1/8, c2 = 7/8 哪一个模型更好的接近真正的概率分布? D(A|| B)= 1/2log(1/2 / 1/4) + 1/2 log(1/2 / 3/4) D (A || C) = 1/2 log(1/2 / 1/8) + 1/2 log(1/2 /
KL散度(Kullback-Leibler_divergence)
KL-divergence,俗称KL距离,常用来衡量两个概率分布的距离。 1. 根据shannon的信息论,给定一个字符集的概率分布,我们可以设计一种编码,使得表示该字符集组成的字符串平均需要的比特数最少。假设这个字符集是X,对x∈X,其出现概率为P(x),那么其最优编码平均需要的比特数等于这个字符集的熵: a.当log以2为底的时候称之为 bits,结果可以视为多少个二进制位