coordinate专题

2020ICPC 南京 Evil Coordinate（模拟，构造）

最后是队友过的，我写的相对复杂题意：给一个移动的序列（L,R,U,D代表左右上下），重排其使得移动的过程不会经过 ( X , Y ) (X,Y) (X,Y)。设终点为 ( e x , e y ) (ex,ey) (ex,ey) 思路：首先特判掉特殊点为终点或者为原点的情况，分为两种情况：特殊点不在坐标轴上，此时如果 e x = X ex=X ex=X,那么先用 L , R L,

YOLOv9/YOLOv8算法改进【NO.105】对Coordinate Attention进行二次创新构建新模块

前言 YOLO算法改进系列出到这，很多朋友问改进如何选择是最佳的，下面我就根据个人多年的写作发文章以及指导发文章的经验来看，按照优先顺序进行排序讲解YOLO算法改进方法的顺序选择。具体有需求的同学可以私信我沟通：首推，是将两种最新推出算法的模块进行融合形成最为一种新型自己提出的模块然后引入到YOLO算法中，可以起个新的名字，这种改进是最好发高水平期刊论文。后续改进将主要教大

[gym102832L][CCPC2020 长春站 L]Coordinate Paper

Coordinate Paper 题解很简单的一道构造题。我们发现，相邻两个数可以转化成 a i + 1 ≡ a i + 1 ( m o d k + 1 ) a_{i}+1 \equiv a_{i+1}(mod\, k+1) ai+1≡ai+1(modk+1)的关系。所以我们可以考虑先构造出一组符合要求的最小解，对于可以向上加的点加上 k + 1 k+1 k+1去构造解，使得这组解

14.图像透视——距离的测验，齐次坐标（Homogeneous Coordinate），透视投影（Perspective Projection），投影实战_2

目录距离的测验齐次坐标（Homogeneous Coordinate）透视投影（Perspective Projection）投影实战学前概念透视投影法(perspective projection method)一种投影法。所谓透视，即穿过透明体观察物体。在人与物体之间，设立一个透明的平面，称作画面(即投影面)，人眼的位置称视点(即投影中心COP)，由视点至物体上各个

重要概念----Reference Coordinate System--参考坐标系

参考坐标系（Reference Coordinate System）列表是让你指定用于变换（移动move、旋转rotate和缩放scale）的坐标系。选项包括视图坐标view，屏幕坐标screen，世界坐标world，父坐标parent，局部坐标local，网格坐标grid和拾取坐标pick。在屏幕坐标系下，所有的视图（包括透视图perspective）使用视口屏幕坐标。视图

OpenGL学习笔记8-Coordinate Systems

Coordinate Systems（坐标系） Getting-started/Coordinate-Systems（开始/坐标系统）在上一章中，我们学习了如何利用矩阵来转换所有的顶点。OpenGL期望在每个顶点着色器运行后，我们想要变得可见的所有顶点都在规范化的设备坐标中。也就是说，每个顶点的x、y、z坐标应该在-1.0到1.0之间;超出此范围的坐标将不可见。我们通常做的是，指定我们自己确

论文解读：Coordinate Attention for Efficient Mobile Network Design(CVPR2021)

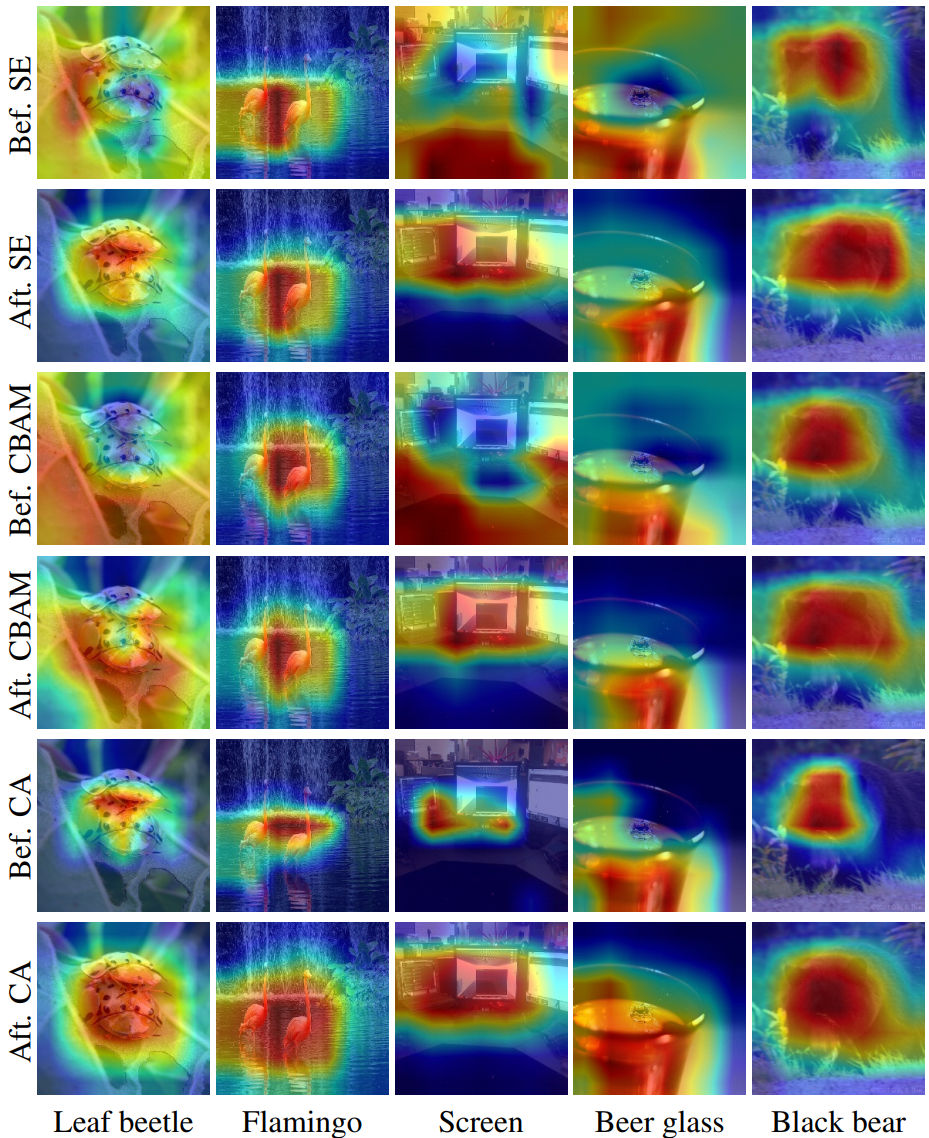
论文前言原理其实很简单，但是论文作者说得很抽象，时间紧的建议直接看3.1中原理简述CBMA、原理简述CBMA以及3.2中原理简述coordinate attention block即可。 Abstract 最近关于mobile network设计的研究已经证明了通道注意(例如，the Squeeze-and-Excitation attention)对于提高模型性能的显着有效性，但

CVPR2021| 继SE,CBAM后的一种新的注意力机制:坐标注意力机制（Coordinate Attention）

一、前言论文：http://arxiv.org/abs/2103.02907论文：http://arxiv.org/abs/2103.02907 论文：源码：https://github.com/Andrew-Qibin/CoordAttention 在本文中提出了一种新颖且高效的注意力机制，通过嵌入位置信息到通道注意力，从而使移动网络获取更大区域的信息而避免引入大的开销

齐次坐标 (Homogeneous Coordinate)

转载：http://www.360doc.com/content/11/0410/18/3698714_108650801.shtml（非源出处）齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射（线性）几何变换。”—— F.S. Hill, JR。对于一个向量v以及基oabc，可以找到一组坐标(v1,v2,v3)，使得v = v1 a +

Distribution-Aware Coordinate Representation for Human Pose Estimation阅读笔记

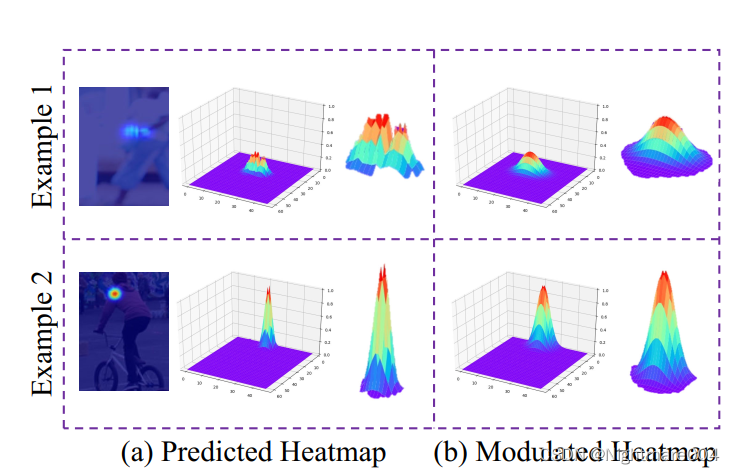
主要研究人体姿态估计中heatmap转坐标的方法，提出一种新的解码方法（其实这人体姿态我毛也不会，过来看看这个heatmap解码方法）代码：https://github.com/ilovepose/DarkPose/blob/master/lib/core/inference.py 方法人体姿态估计简单来说就是要预测人的所有关节的坐标，这里主要研究把关节转为热体图，然后进行回归的那种方

Isometric Coordinate Calculation Tutorial

现在我们来看在isometric game中如何从屏幕坐标(screen coordinate)计算地图坐标(map coordinate) 首先我们需要在我们的等角系统(isometric system)中先解释一些定义和约定. [b]坐标系统(Coordinate Systems)[/b] 我们要计算两个坐标系统,第一个是地图坐标系统(Map coordinate system),可

【翻译】Coordinate Attention for Efficient Mobile Network Design

Coordinate Attention for Efficient Mobile Network Design 高效移动网络设计的坐标关注力 Qibin Hou, Daquan Zhou, Jiashi Feng 论文：Coordinate Attention for Efficient Mobile Network Design 项目：https://github.com/Andrew-Qi

Part I 空气曲棍球 Chapter5 (5.2 Working with a Virtual Coordinate Space)

5.2 虚拟坐标系（Working with a Virtual Coordinate Space）为了适配屏幕旋转的情况，我们需要调整之前使用的坐标空间，如何调整呢？那就是不能直接使用规范化设备坐标而是需要调整会使用虚拟坐标空间。为了使用OpenGL能够正确的进行渲染，我们需要找一种把虚拟坐标空间转换到规范化坐标空间的方法。而为了使用我们的球台桌面的竖屏与横屏情况下都得到正确的显示，

神经网络学习小记录73——Pytorch CA（Coordinate attention）注意力机制的解析与代码详解

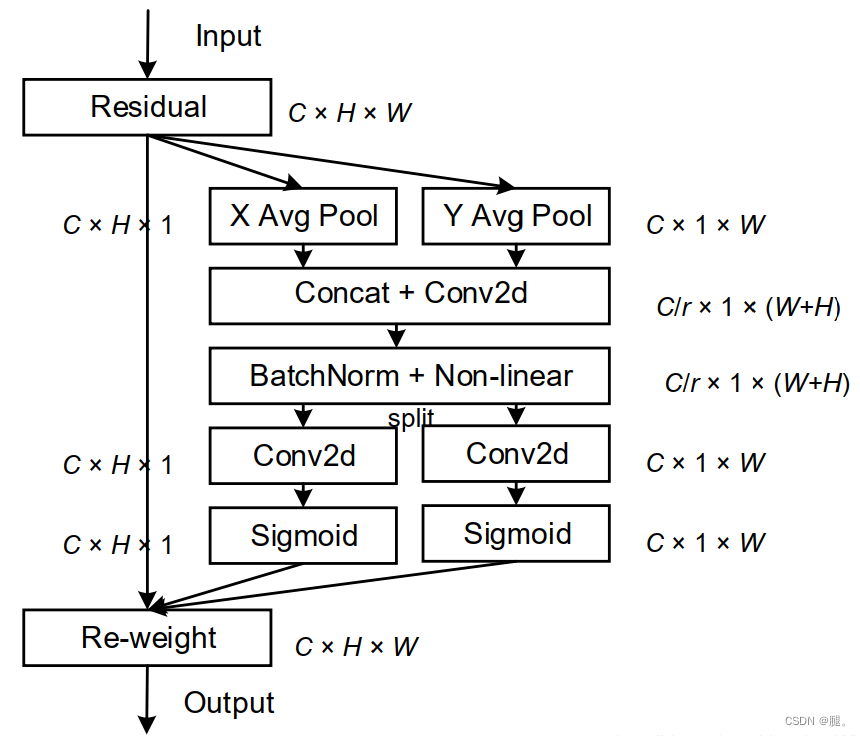
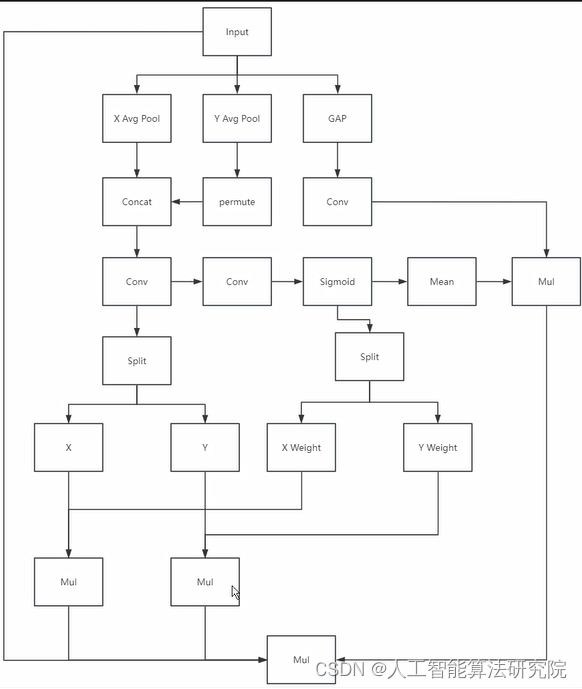
神经网络学习小记录73——Pytorch CA（Coordinate attention）注意力机制的解析与代码详解学习前言代码下载CA注意力机制的概念与实现注意力机制的应用学习前言 CA注意力机制是最近提出的一种注意力机制，全面关注特征层的空间信息和通道信息。代码下载 Github源码下载地址为： https://github.com/bubbliiiing/yol

坐标旋转数字计算法（Coordinate Rotation Digital Computer, CORDIC）

目录 1. CORDIC原理2. 圆周系统2.1. 迭代算法预旋转旋转模式—— y = c o s ( x ) y=cos(x) y=cos(x) and y = s i n ( x ) y=sin(x) y=sin(x) 2.2. 向量模式—— y = a r c t a n ( x ) y=arctan(x) y=arctan(x) and l = x 2 + y 2 l=\sqrt