本文主要是介绍day 38 435.无重叠区间 763.划分字母区间 56. 合并区间 738.单调递增的数字 968.监控二叉树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
435.无重叠区间
思路
为了使区间尽可能的重叠所以排序来使区间尽量的重叠,使用左边界排序来统计重叠区间的个数与452. 用最少数量的箭引爆气球恰好相反。
代码
class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals,(a,b)->Integer.compare(a[0],b[0]));int count = 0;for (int i = 1; i < intervals.length; i++) {if(intervals[i-1][1] > intervals[i][0]){count++;intervals[i][1] = Math.min(intervals[i-1][1],intervals[i][1]);}}return count;}
}763.划分字母区间
思路
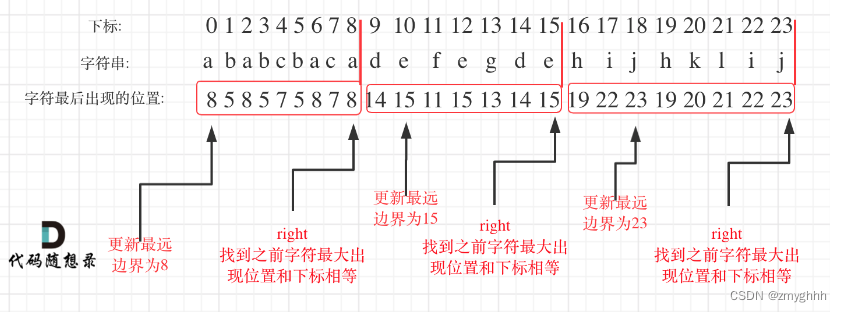
首先想到了回溯但是使用回溯依然没有思路,在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
可以分为如下两步:
- 统计每一个字符最后出现的位置
- 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
代码
class Solution {public List<Integer> partitionLabels(String s) {List<Integer> list = new LinkedList<>();int [] hash = new int[27];char [] chars = s.toCharArray();for (int i = 0; i < chars.length; i++) {hash[chars[i] - 'a'] = i;}int left = 0,right = 0 ;for (int i = 0; i < chars.length; i++) {right = Math.max(right , hash[chars[i] - 'a']);if(i == right){list.add(right -left +1);left = i+1;}}return list;}
}56. 合并区间
思路
本题的本质其实还是判断重叠区间问题。452. 用最少数量的箭引爆气球 (opens new window)和 435. 无重叠区间都是判断区间重叠,区别就是判断区间重叠后的逻辑,本题是判断区间重贴后要进行区间合并。

代码
class Solution {public int[][] merge(int[][] intervals) {LinkedList<int[]> res = new LinkedList<>();Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));res.add(intervals[0]);for (int i = 1; i < intervals.length; i++) {if (intervals[i][0] <= res.getLast()[1]) {int start = res.getLast()[0];int end = Math.max(intervals[i][1], res.getLast()[1]);res.removeLast();res.add(new int[]{start, end});}else {res.add(intervals[i]);}}return res.toArray(new int[res.size()][]);}
}738.单调递增的数字
思路
贪心算法
例如98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]--,然后strNum[i]给为9,这样这个整数就是89,即小于98的最大的单调递增整数。
此时是从前向后遍历还是从后向前遍历呢?
从前向后遍历的话,遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]减一,但此时如果strNum[i - 1]减一了,可能又小于strNum[i - 2]。
数字:332,从前向后遍历的话,那么就把变成了329,此时2又小于了第一位的3了,真正的结果应该是299。
那么从后向前遍历,就可以重复利用上次比较得出的结果了,从后向前遍历332的数值变化为:332 -> 329 -> 299
class Solution {public int monotoneIncreasingDigits(int n) {String s = String.valueOf(n);char[] chars = s.toCharArray();int start = s.length();for (int i = s.length() - 2; i >= 0; i--) {if (chars[i] > chars[i + 1]) {chars[i]--;start = i+1;}}for (int i = start; i < s.length(); i++) {chars[i] = '9';}return Integer.parseInt(String.valueOf(chars));}
}968.监控二叉树
思路
题目示例中的摄像头都没有放在叶子节点上!这是很重要的一个线索,摄像头可以覆盖上中下三层,如果把摄像头放在叶子节点上,就浪费的一层的覆盖。
所以把摄像头放在叶子节点的父节点位置,才能充分利用摄像头的覆盖面积。
为什么不从头结点开始看起呢,为啥要从叶子节点看呢?
因为头结点放不放摄像头也就省下一个摄像头, 叶子节点放不放摄像头省下了的摄像头数量是指数阶别的。(也算是一个贪心)
局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,
整体最优:全部摄像头数量所用最少!
思路就是从低到上,先给叶子节点父节点放个摄像头,然后隔两个节点放一个摄像头,直至到二叉树头结点。
在二叉树中如何从低向高推导呢?
可以使用后序遍历也就是左右中的顺序,这样就可以在回溯的过程中从下到上进行推导了。左孩子的返回值,右孩子的返回值,即left 和 right, 以后推导中间节点的状态
难点
每个节点可能有几种状态:
有如下三种:
- 该节点无覆盖(无摄像头)
- 本节点有摄像头
- 本节点有覆盖(无摄像头)
空节点的状态只能是有覆盖
为了让摄像头数量最少,我们要尽量让叶子节点的父节点安装摄像头,这样才能摄像头的数量最少。
那么空节点不能是无覆盖的状态,这样叶子节点就要放摄像头了,空节点也不能是有摄像头的状态,这样叶子节点的父节点就没有必要放摄像头了,而是可以把摄像头放在叶子节点的爷爷节点上。
主要有如下四类情况:
- 情况1:左右节点都有覆盖
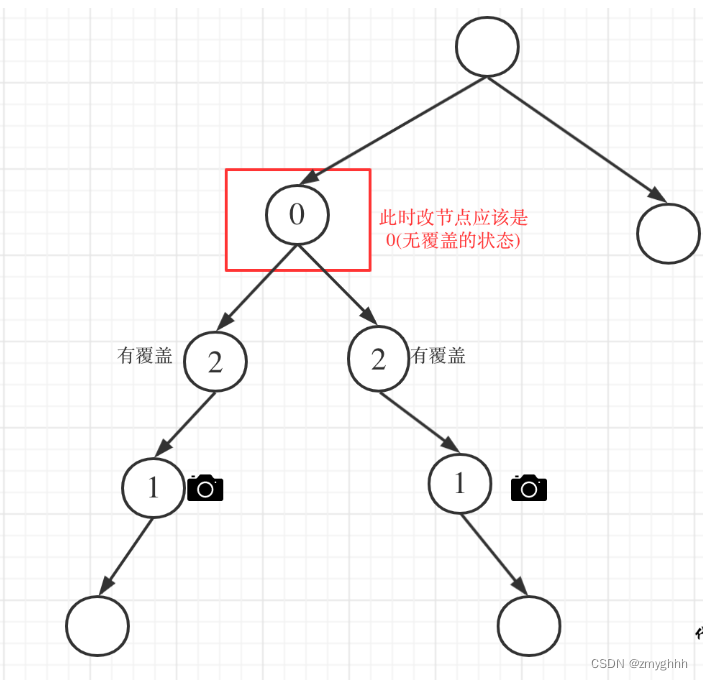
- 情况2:左右节点至少有一个无覆盖的情况:中间节点(父节点)应该放摄像头
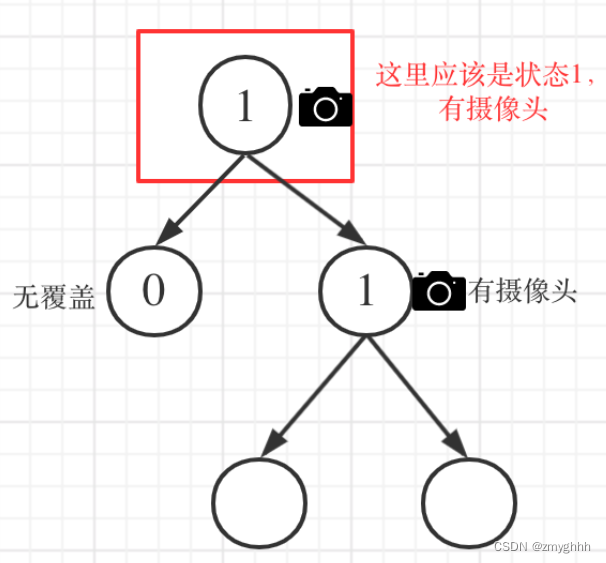
如果left == 1, right == 0 怎么办?其实这种条件在情况2中已经判断过了,如图:
- 情况3:左右节点至少有一个有摄像头:左右孩子节点有一个有摄像头了,那么其父节点就应该是2(覆盖的状态)
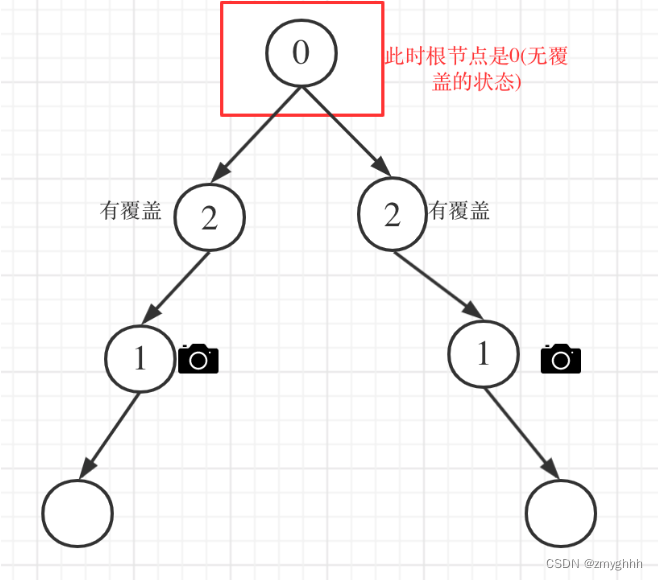
- 情况4:头结点没有覆盖
代码
class Solution {int result = 0 ;public int minCameraCover(TreeNode root) {if(traversal(root) == 0){result++;}return result;}/**节点的状态值:0 表示无覆盖1 表示 有摄像头2 表示有覆盖后序遍历,根据左右节点的情况,来判读 自己的状态*/public int traversal(TreeNode root){if(root == null) return 2;int left = traversal(root.left);int right = traversal(root.right);if(left==2 && right==2) return 0;if(left == 0 || right ==0){result++;return 1;}if(left == 1 || right ==1){return 2;}return -1;}
}这篇关于day 38 435.无重叠区间 763.划分字母区间 56. 合并区间 738.单调递增的数字 968.监控二叉树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






