非平稳信号的傅里叶变换与短时傅里叶变换

本文主要是介绍非平稳信号的傅里叶变换与短时傅里叶变换，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、仿真一个非平稳的时间序列。

N = 10000;
t = 0:N-1;
z1 = 4.2*sin(2*pi/20.*t+5);
z2 = 2.2*sin(2*pi/100.*(1+0.001*t).*t+8);
w1 = randn(length(t),1)';
y=z1+z2+w1;
figure;plot(y,'LineWidth',1.5);grid on;
ylabel('Signal');
xlabel('Time');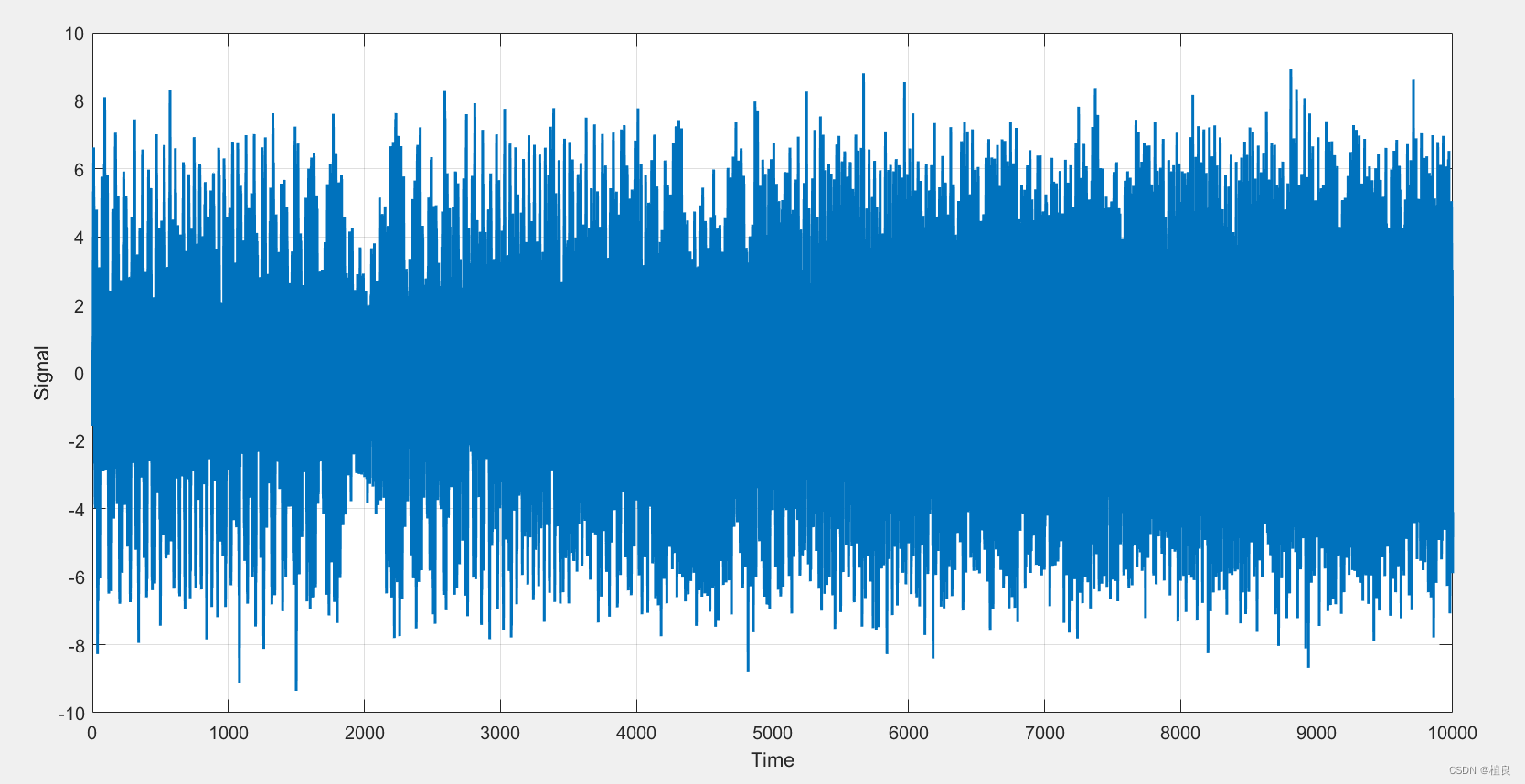

 

二、傅里叶变换（FFT）分析

Fs = 1;
Y = fft(y);
L=length(y);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
%--横坐标是频率--
figure;plot(f,P1,'LineWidth',1.5);grid on; 
title('Single-Sided Amplitude Spectrum of X(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')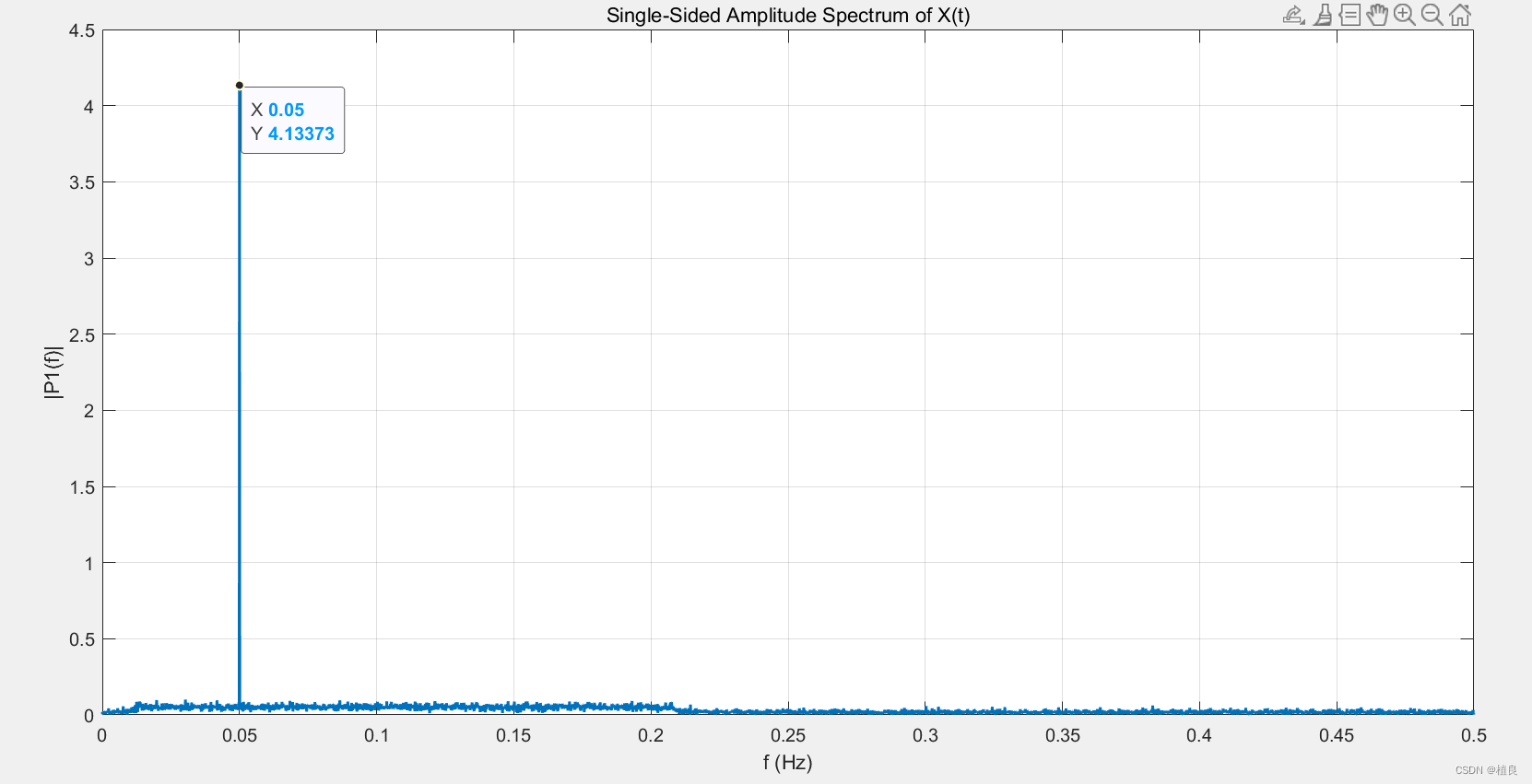

(1)这里横坐标是频率f(hz)，1/0.05=20，对应信号z1周期，如果想将横坐标转换为周期，绘图语句转换为如下即可：

plot(1./f,P1,'LineWidth',1.5);

(2)对于非平稳信号z2，在FFT图中几乎看不出来。

三、短时傅里叶变换（STFT）分析

window=256;
noverlap=16;
nfft=128;
figure;spectrogram(y,window,noverlap,nfft,Fs,'yaxis');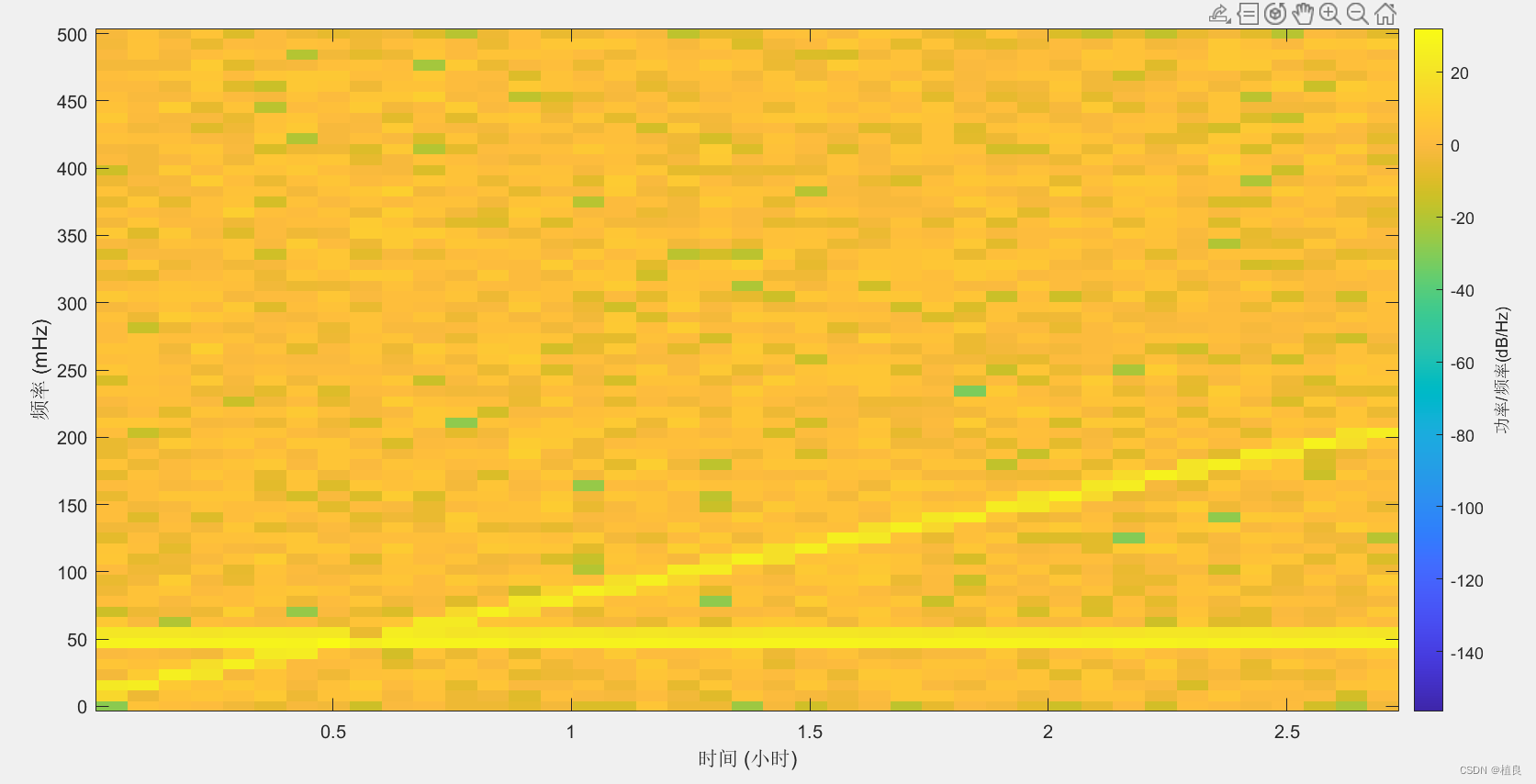

可以改变

window=256;
noverlap=16;
nfft=128;

这些参数，对比分析效果。

如果想根据spectrogram()函数的输出自己绘图，如下：

[scalar,fs,ts] = spectrogram(y,window,noverlap,nfft,Fs);
figure;
pcolor(ts,1./fs,abs(scalar));shading interp;
colorbar
ylabel('Period');
xlabel('Time');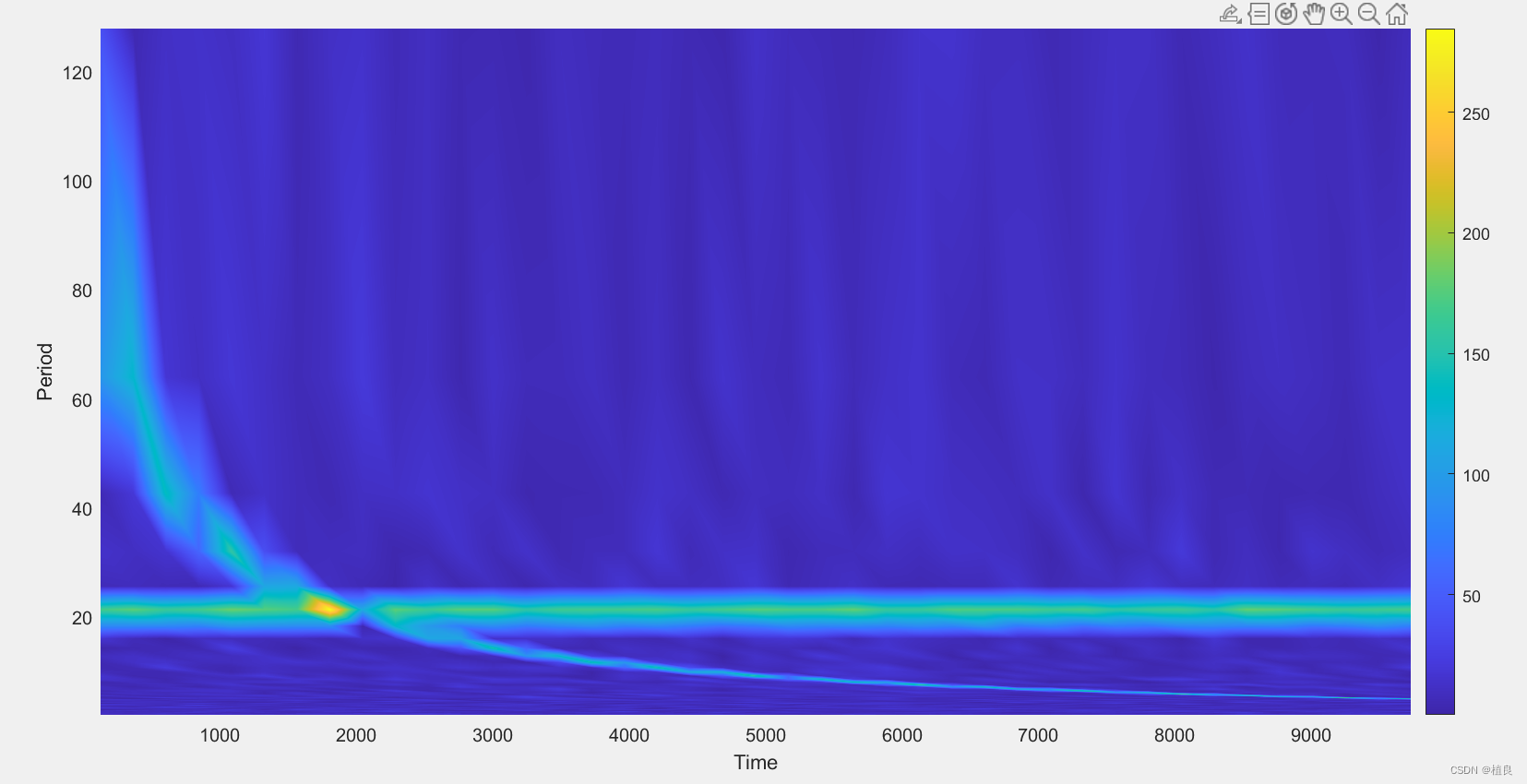

注意：

pcolor(ts,1./fs,abs(scalar));shading interp;

语句中的1./fs将频率转换为了周期。

这篇关于非平稳信号的傅里叶变换与短时傅里叶变换的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---