本文主要是介绍过度拟合与欠拟合,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
偏差和方差的定义介绍:
偏差(Bias)
这里的偏指的是 偏离 , 那么它偏离了什么到导致了误差? 潜意识上, 当谈到这个词时, 我们可能会认为它是偏离了某个潜在的 “标准”, 而这里这个 “标准” 也就是真实情况 (ground truth). 在分类任务中, 这个 “标准” 就是真实标签 (label).
通俗的说就是:
偏差度量了学习算法的期望预测与真实结果的偏离程序, 即 刻画了学习算法本身的拟合能力 .
方差(Variance)
很多人应该都还记得在统计学中, 一个随机变量的方差描述的是它的离散程度, 也就是该随机变量在其期望值附近的 波动程度 . 取自维基百科一般化的方差定义:
也就是说:
方差度量了同样大小的训练集的变动所导致的学习性能的变化, 即 刻画了数据扰动所造成的影响
如果 X 是一个向量其取值范围在实数空间Rn,并且其每个元素都是一个一维随机变量,我我们就称 X 为随机向量。随机向>量的方差是一维随机变量方差的自然推广,其定义为E[(X−μ)(X−μ)T],其中μ=E(X), XT是 X 的转置.
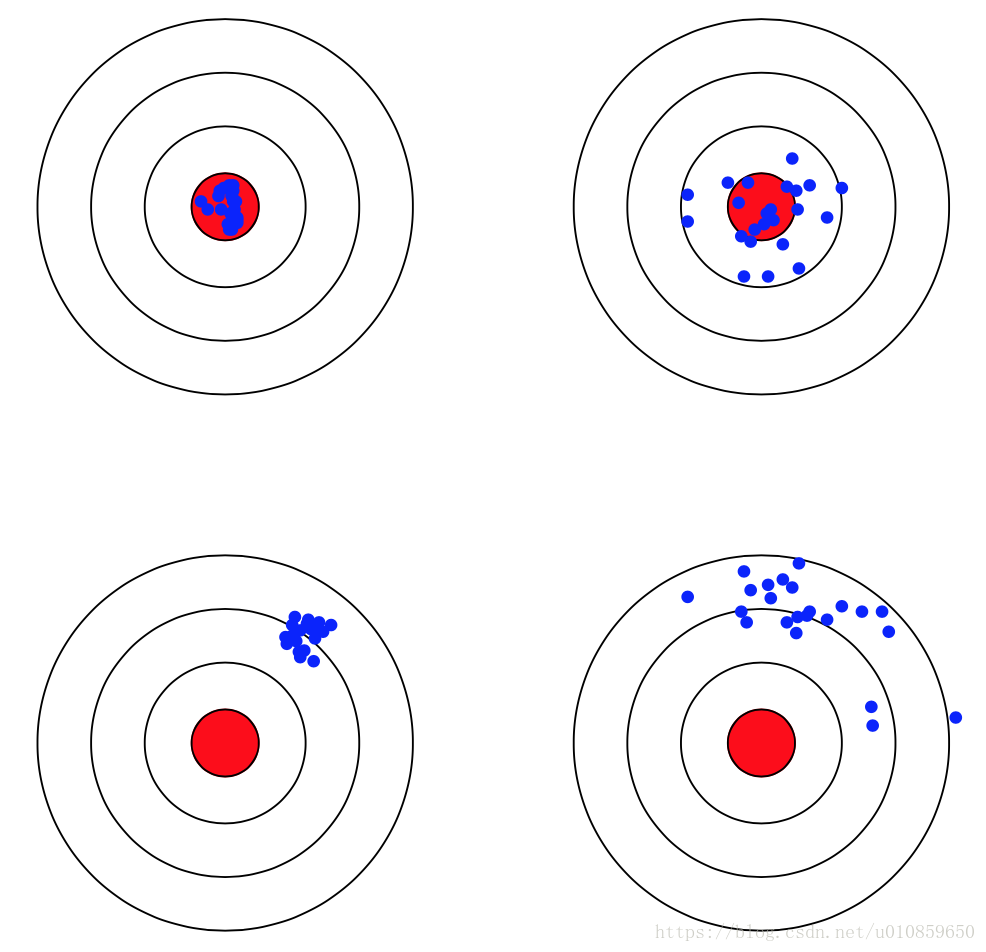
假设红色的靶心区域是学习算法完美的正确预测值, 蓝色点为每个数据集所训练出的模型对样本的预测值, 当我们从靶心逐渐向外移动时, 预测效果逐渐变差.
很容易看出有两副图中蓝色点比较集中, 另外两幅中比较分散, 它们描述的是方差的两种情况. 比较集中的属于方差小的, 比较分散的属于方差大的情况.
再从蓝色点与红色靶心区域的位置关系, 靠近红色靶心的属于偏差较小的情况, 远离靶心的属于偏差较大的情况.
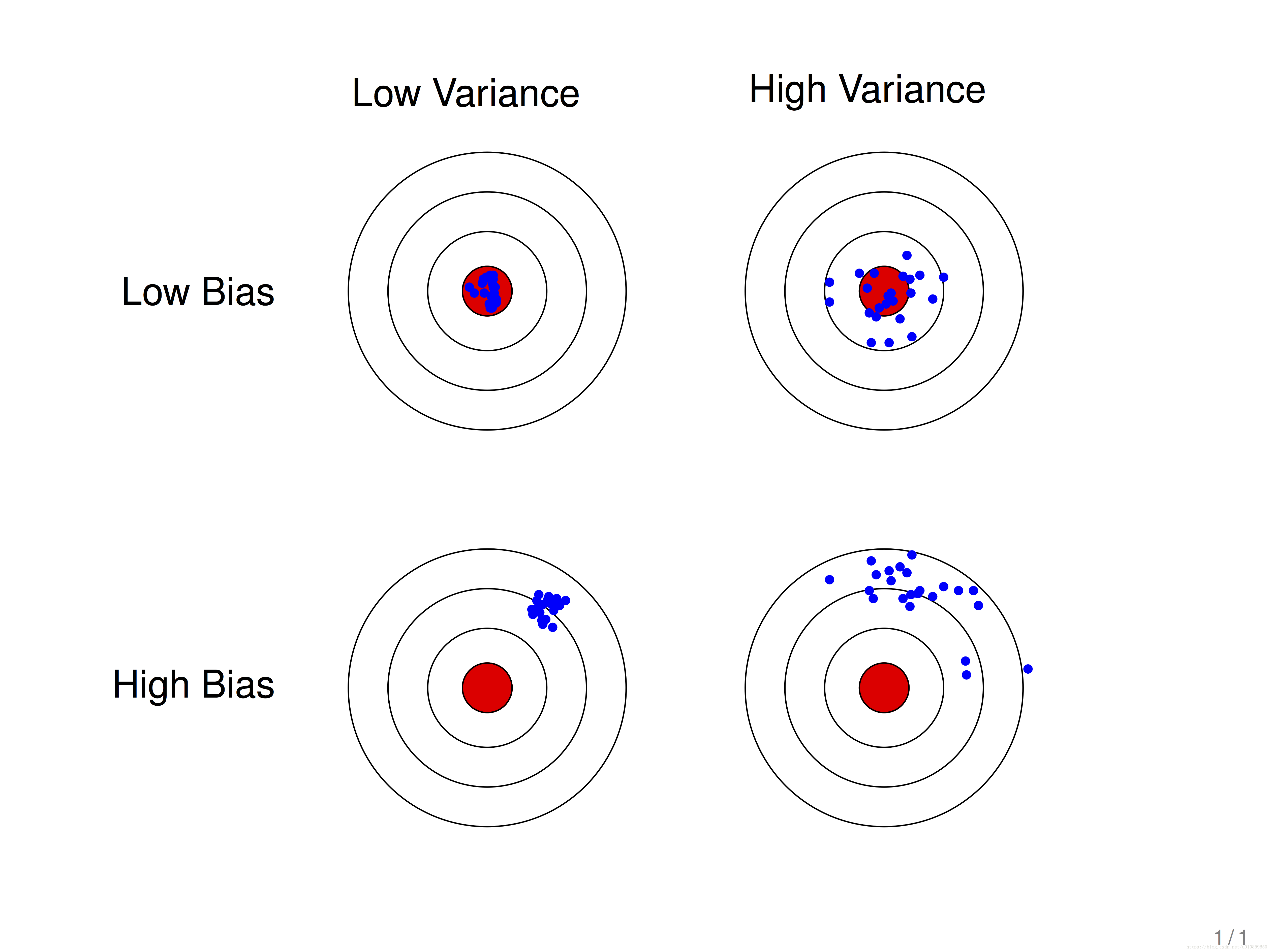
图中的红色位置就是真实值所在位置,蓝色的点是算法每次预测的值。
可以看出,偏差越高则离红色部分越远,而方差越大则算法每次的预测之间的波动会比较大。
具体参考:https://blog.csdn.net/simple_the_best/article/details/71167786
过度拟合与欠拟合
拟合概念
形象的说,拟合就是把平面上一系列的点,用一条光滑的曲线连接起来。因为这条曲线有无数种可能,从而有各种拟合方法。拟合的曲线一般可以用函数表示,根据这个函数的不同有不同的拟合名字
假设一个识别狗算法分类器:
过拟合
训练集错误率:1%测试集错误率:15%偏差为:1% 方差为:15%-1%=14% 总误差为 15%虽然分类器训练误差非常低,但是没能成功泛化到测试集。这叫做过拟合。
欠拟合
训练集错误率:15%测试集错误率:16%偏差为:15% 方差为:1% 总误差: 16%该分类器具有高偏差和高方差。在训练集和测试集上面都表现的很差。这叫做欠拟合。
最后一种情况
训练集错误率:0.5%测试集错误率:1%偏差:0.5% 方差:0.5% 总误差 1%训练集和测试集的都具有低方差和低偏差,分类器表现很好。
模型修改策略
过拟合:增大数据规模、减小数据特征数(维数)、增大正则化系数λ
欠拟合:增多数据特征数、添加高次多项式特征、减小正则化系数λ
这篇关于过度拟合与欠拟合的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!