本文主要是介绍YOLO损失函数——SIoU和Focal Lossr损失函数解析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 概述

YOLO(You Only Look Once) 系列模型以其实时目标检测能力而闻名,其有效性在很大程度上归功于其专门设计的损失函数。在本文中,这里将深入探讨YOLO演进中不可或缺的各种YOLO损失函数,并重点介绍它们在PyTorch中的实现。
通过探索这些函数背后的代码,读者可以为自己的深度学习项目获得实用的见解,增强开发高级目标检测模型的能力。具体来说,这里将回顾在YOLOv6和YOLOv8中使用的Focal Loss和SIoU Loss。在下一部分中,将讨论分布式Focal Loss(DFL)和变焦Focal Loss(VFL)。
YOLO模型的损失函数旨在优化目标检测任务的多个方面,包括分类损失、定位损失和置信度损失。每个版本的YOLO都引入了新的损失函数或对现有损失函数进行了改进,以提高检测的精度和速度。
Focal Loss
Focal Loss 是为了解决类别不平衡问题而提出的损失函数。传统的交叉熵损失在处理大量负样本时可能会使模型训练不稳定,而Focal Loss通过引入一个调节因子,降低了简单样本的权重,从而使模型更专注于难分类的样本。
SIoU Loss
SIoU Loss(Scalable Intersection over Union Loss) 是一种改进的IoU损失,旨在提供更平滑和更鲁棒的梯度。它在计算IoU的基础上,考虑了边界框的尺度和角度信息,以提高定位的精度和鲁棒性。
2. 损失函数的重要性
深度学习模型通常被视为一个高维映射函数,它接受输入并生成预测。为了判断预测的准确性,我们使用损失函数或成本函数。这是一个数学函数,用于衡量预测值与真实值之间的偏差。然后,我们利用优化器(例如随机梯度下降或自适应矩估计(ADAM))根据估计的损失来更新模型参数。损失函数通常分为两种类型:凸损失和非凸损失函数。下面我们将详细讨论这两种类型。
如果你通过选择函数图形上的任意两个不同点,并且通过这两个点的直线在图形上不与其它点相交,那么这个函数可以被视为凸函数。凸函数的一个独特属性是它只有一个全局最小值。
**示例:**均方误差(MSE)、Hinge损失、交叉熵损失等是凸损失函数的例子。

图1:凸和非凸损失函数
非凸函数
非凸函数与凸函数的定义相对立,其特性在几何上表现为:
如果在函数图形上任意选择两个不同的点并连接它们,所形成的线段如果在函数图形的其它部分有交点,那么这个函数就被称为非凸函数。
这种特性导致了非凸函数可能在多个点上具有局部最小值。由于存在多个局部最小值,而非凸优化问题可能难以找到全局最小值,这使得非凸函数的优化问题比凸函数的优化问题更具挑战性。
示例:
- 三重损失(Triplet Loss):在深度学习中,尤其是在训练具有大量不同类别的数据集时,三重损失被用来拉近不同类别之间的距离,同时推远同类样本之间的距离。
- 带有softmax激活的负对数似然(Negative Log Likelihood with Softmax Activation):这是分类问题中常用的损失函数之一,特别是在使用softmax函数作为激活函数时。softmax函数将输入转换为概率分布,负对数似然衡量的是模型预测的概率分布与真实标签的概率分布之间的差异。
3.YOLO损失函数
在YOLO(You Only Look Once)目标检测框架中,损失函数的设计对于模型性能至关重要。YOLO模型的损失函数主要分为两大类:分类损失和回归损失。
3.1 YOLO损失函数
分类损失和回归损失构成了YOLO模型中损失函数的主体。在YOLOv1中,目标检测问题被创新性地表述为一个回归问题,这一创新是YOLO系列模型的基石。直到YOLOv3,模型主要采用平方损失来处理边界框回归,同时使用交叉熵损失来处理目标分类任务。
然而,从YOLOv4开始,研究者们开始转向更多地关注基于IoU(交并比)的损失函数。IoU是一个衡量预测边界框与真实边界框重叠程度的指标,它为边界框定位精度提供了一个更准确的估计。
3.2 CIoU和SIoU损失
- CIoU (Complete IoU):YOLOv5、YOLOv4、YOLOR和YOLOv7的作者采用了CIoU损失作为边界框回归的损失函数。CIoU损失考虑了边界框的对齐和尺度,是对传统IoU损失的一个改进。
- SIoU/GIoU:YOLOv6引入了SIoU(Shape-Aware IoU)或GIoU(Generalized Intersection over Union)损失,这些损失函数进一步考虑了形状和方向,以提高边界框预测的准确性。
3.3 VariFocal损失和DFL
- VariFocal损失:在YOLOX中,作者选择了传统的IoU损失,同时引入了VariFocal损失来处理分类任务,这一损失函数能够更好地处理极端类别不平衡问题。
- 分布Focal损失(DFL):YOLOv8采用了CIoU损失和DFL,后者是一种针对边界框回归的新型损失函数,它考虑了边界框的分布特性。
3.4 YOLO模型的演进
YOLO系列模型作为最先进的目标检测模型,其不断的演进和改进对于机器视觉领域具有重要意义。了解不同YOLO模型的设计理念和损失函数的使用,对于研究人员和开发者来说是非常宝贵的。
- YOLOv5自定义训练:提供了在自定义数据集上训练YOLOv5的全面指南,这对于希望将YOLO模型应用于特定问题的用户来说是一个重要的资源。
- YOLOv6论文解释:对YOLOv6的设计理念和架构进行了深入的分析和讨论。
- YOLOv8自定义模型训练:YOLOv8作为系列中的重要模型,其自定义模型训练的深入讨论有助于理解如何根据特定需求调整和优化YOLO模型。
4. SCYLLA IoU (SIoU) Loss
SIoU是一种独特的损失函数,涉及四种不同的成本函数,如:
- 角度成本
- 距离成本
- 形状成本
- IoU成本
在使用基于卷积的架构时,研究表明SIoU提高了训练速度和模型准确性。作者声称方向性是这些改进的主要原因。以下是每个SIoU损失函数的详细解释,
4.1 角度成本
这是角度感知损失函数部分,有助于提高训练速度和准确性。它有助于减少模型复杂性,特别是解决在预测与距离相关的变量时的“徘徊”问题。这里,“徘徊”指的是变化的边界框预测问题。拥有太多的自由度可能会导致这个问题。DoF定义为在3D空间中移动一个刚体的基本方式的数量。让我们看一些示例来理解自由度(DoF)。一个刚体在3D空间中的DoF是什么?它有6个DoF:x、y、z、绕X轴旋转角度(roll)、绕Y轴旋转角度(pitch)和绕Z轴旋转角度(yaw)。类似地,一个2D边界框有4个DoF,x、y(用于中心点)和边界框的宽度(w)和高度(h),角度成本的公式是:
(a) 角度成本公式;(b) 角度成本直觉图:
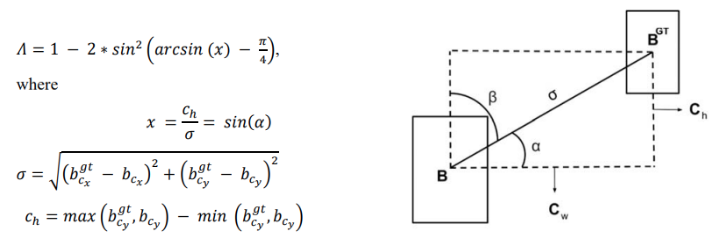
给定预测和真实边界框,水平轴和连接每个框中心的线之间的角度被视为 a a a与垂直轴的角度被视为 β , C h \beta,C_h β,Ch是两个边界框中心的垂直距离。上述损失函数类似于一个三角函数 c c o s ( 2 x ) = 1 − 2 sin 2 ( x ) ccos(2\mathbf{x})\,=\,1\,-\,2\,\sin^{2}\,(x) ccos(2x)=1−2sin2(x)。成本利用了 a a a和 β \beta β ,模型试图最小化 a a a如果 α < π 4 \alpha\lt {\frac{\pi}{4}} α<4π否则它最小化 ,其中 β = π 4 − α \beta={\frac{\pi}{4}}-\alpha β=4π−α。
4.2 距离成本
距离成本的设计宗旨是在角度成本的基础上进行优化。其核心理念是,随着预测边界框与真实边界框之间角度差的增加,距离误差对于总体损失的贡献应该显著降低。这样的设计动机是为了促使预测边界框在空间位置上更紧密地贴近真实边界框。
论文中的表述强调了这一策略的重要性:“因此,随着角度差的增加,距离值的优化在计算中被赋予了较低的优先级。” 这表明,在评估损失时,较小的角度偏差相较于较大的角度偏差,其对应的距离偏差会被视为较轻微的错误,因而受到的惩罚也相对较小。这种机制允许模型在面对较大角度偏差时,优先调整边界框的方向,而非仅仅追求空间位置的接近,从而在整体上提升了模型预测的准确性。
© 距离成本公式;(d) 距离成本图:
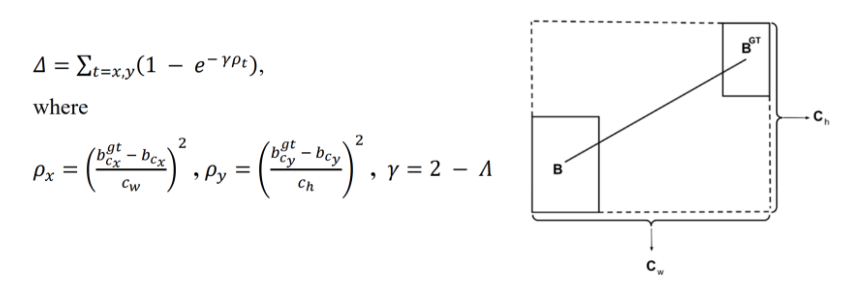
其中, b c x g t , b c x = x {\mathfrak{b}}_{c x}^{g t},{\mathfrak{b}}_{c x}=x bcxgt,bcx=x真实和预测边界框的x坐标, b c y g t , b c y = y {\mathfrak{b}}_{c y}^{g t},{\mathfrak{b}}_{c y}=y bcygt,bcy=y真实和预测边界框的y坐标 C w , C h = C_w,C_h = Cw,Ch=最小外接盒或“凸盒”的宽度和高度, C w C_w Cw和 C h C_h Ch在图 d d d中已注释。
4.3形状成本
形状成本是处理纵横比不匹配的部分。它定义为,(e) 形状成本公式;(f) 形状成本图:
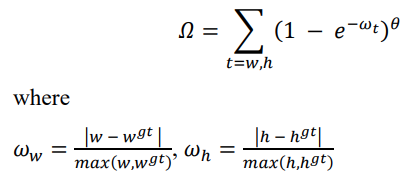
其中, w w w和 w g t = w^{gt} = wgt=预测和真实边界框的宽度, h h h和 h g t = h^{gt}= hgt=预测和真实边界框的高度,分别。 w w w_w ww和 w h = w_h= wh=两个边界框宽度和高度的相对差异。
4.4 IoU成本
IoU成本是普通的交集比并集值减去1。通过减去1的IoU值,强调了预测边界框的非重叠部分。
L I o U = 1 − I o U L_{IoU} = 1 - IoU LIoU=1−IoU
I o U = ∣ B ∩ B G T ∣ ∣ B ∪ B G T ∣ I o U={\frac{\left|B\cap B^{G T}\right|}{\left|B\cup B^{G T}\right|}} IoU=∣B∪BGT∣ B∩BGT
SIoU损失是使用距离成本、形状成本和IoU成本定义的。角度成本在距离成本中使用。以下是SIoU公式:
L b o x = 1 − I o U + Δ + A 2 L_{b o x}=1\,-\,I o U+{\frac{\Delta\,+\,\mathcal{A}}{\mathcal{2}}} Lbox=1−IoU+2Δ+A
5. 代码实现
5.1 SIoU PyTorch实现
import torch
import torch.nn as nn
import numpy as npclass SIoU(nn.Module):# SIoU Loss https://arxiv.org/pdf/2205.12740.pdfdef __init__(self, x1y1x2y2=True, eps=1e-7):super(SIoU, self).__init__()self.x1y1x2y2 = x1y1x2y2self.eps = epsdef forward(self, box1, box2):# 获取边界框的坐标if self.x1y1x2y2: # x1, y1, x2, y2 = box1b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]else: # 从xywh转换为xyxyb1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2# 交集面积inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \(torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)# 并集面积w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + self.epsw2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + self.epsunion = w1 * h1 + w2 * h2 - inter + self.eps# 边界框的IoU值iou = inter / unioncw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1) # 凸盒(最小外接盒)宽度ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1) # 凸盒高度s_cw = (b2_x1 + b2_x2 - b1_x1 - b1_x2) * 0.5s_ch = (b2_y1 + b2_y2 - b1_y1 - b1_y2) * 0.5sigma = torch.pow(s_cw ** 2 + s_ch ** 2, 0.5) + self.epssin_alpha_1 = torch.abs(s_cw) / sigmasin_alpha_2 = torch.abs(s_ch) / sigmathreshold = pow(2, 0.5) / 2sin_alpha = torch.where(sin_alpha_1 > threshold, sin_alpha_2, sin_alpha_1)# 角度成本angle_cost = 1 - 2 * torch.pow(torch.sin(torch.arcsin(sin_alpha) - np.pi/4), 2)# 距离成本rho_x = (s_cw / (cw + self.eps)) ** 2rho_y = (s_ch / (ch + self.eps)) ** 2gamma = 2 - angle_costdistance_cost = 2 - torch.exp(gamma * rho_x) - torch.exp(gamma * rho_y)# 形状成本omiga_w = torch.abs(w1 - w2) / torch.max(w1, w2)omiga_h = torch.abs(h1 - h2) / torch.max(h1, h2)shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), 4) + torch.pow(1 - torch.exp(-1 * omiga_h), 4)return 1 - (iou + 0.5 * (distance_cost + shape_cost))Focal loss最初是在2017年的论文《Focal Loss for Dense Object Detection》中由He等人引入的。当时,目标检测被视为一个非常困难的问题,特别是如果数据集不平衡或要检测的对象很小。在SSD的领导下,这篇论文试图通过引入一个名为RetinaNet的独特模型架构和一个名为Focal loss的损失函数来同时解决这两个问题。
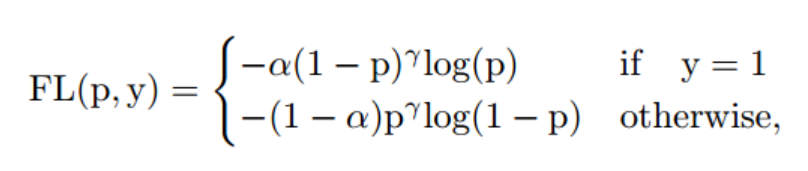
其中, a a a 是权重因子, γ {\gamma} γ是调节因子, p p p是真实类别的概率。
前一代目标检测器通常使用交叉熵损失来解决分类任务。交叉熵的一个特点是它将事物视为二元的,白色和黑色,没有中间的灰色。换句话说,它对正确预测的赞扬和对错误预测的贬低一样多。这在数学上也是正确的,
二元交叉熵和分类交叉熵损失公式:
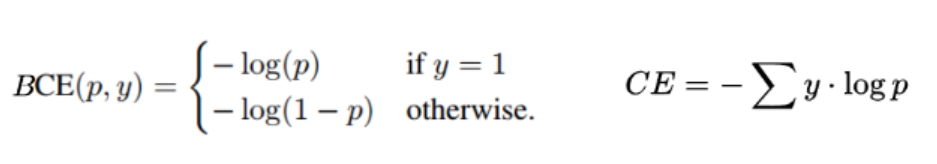
交叉熵定义为概率的负对数。这意味着高概率和低损失。对于损失函数来说,这是一个好属性,为正面和负面样本提供相等的权重。然而,在交叉熵无法带来结果的场景中,以下是一些情况,
- 在类别不平衡的情况下,由多数类计算的梯度对损失函数的贡献更大,导致权重更新在模型更容易检测多数类的方向上。由于少数类在估计损失中的贡献较少,因此更难准确预测它们。
- 难以区分简单和困难的例子。简单的例子是模型犯错误较少的数据点,而困难的例子是模型经常犯大错误的那些。
我们已经了解了交叉熵的失败之处,现在让我们理解focal loss是如何形成的,它帮助解决了交叉熵失败的问题。在论文中提供的图表中,比较了交叉熵损失和focal loss,Focal Loss Function的损失与概率图:
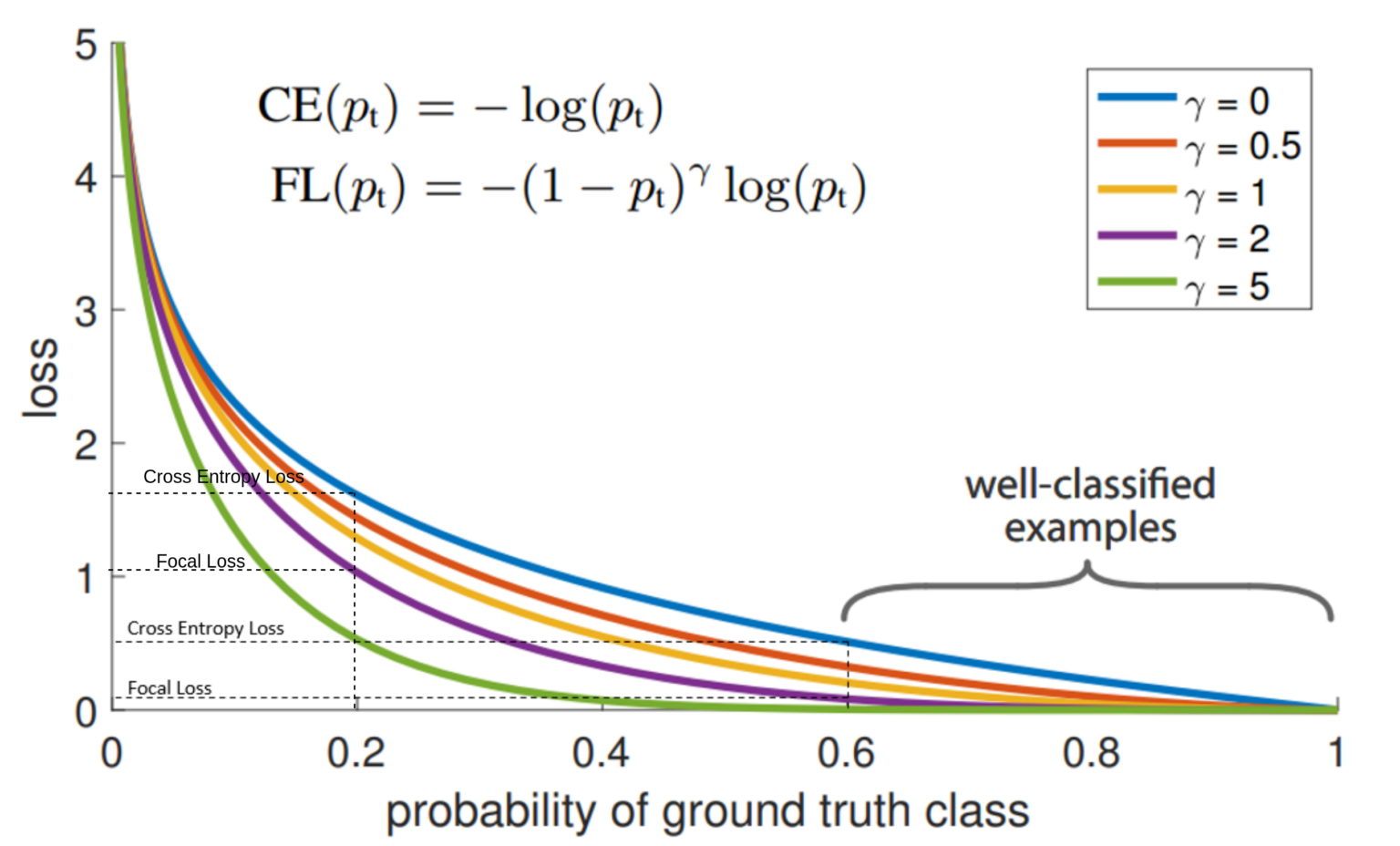
在图中,显示了特定概率值下二元交叉熵和focal loss的损失值的比较。我们将观察两个例子,一个是低概率,一个是高概率,
- 在 p = 0.8 的情况下,BCE Loss接近0.2,Focal Loss接近0.0002。
- 在 p = 0.2 的情况下,BCE Loss接近1.6,Focal Loss接近1。
假设一批中有10个样本,其中8个样本来自多数类,2个样本来自少数类。通常,模型将以高概率(0.8)预测多数类,以低概率(0.2)预测少数类。在focal loss的情况下,与少数类相比,它更急剧地降低了多数类的损失。在多数类的情况下,损失从0.2(CE)下降到0.0002(FL),但在少数类的情况下,损失从1.6(CE)下降到1(FL)。为了调节简单和困难例子的损失贡献,作者引入了调节因子 。focal loss的这个属性解决了上面提到的第二个问题(第2点)。
解决类别不平衡问题的常见方法是为真实类别添加权重因子 α ∈ [ 0 , 1 ] \alpha\in[0,1] α∈[0,1],否则为$(1-a) 。在实践中 , 。在实践中, 。在实践中,a$通过逆类频率设置或作为通过交叉验证设置的超参数。在focal loss之前,在平衡交叉熵论文中引入了类似的方法。
5.2 Focal Loss PyTorch实现
clastargets + (1 - self.alpha) * (1 - targets)
loss = alpha_t * loss
loss = loss.mean()
return lossinputs = torch.randn(10)
targets = torch.randint(1, 5, (10,)).to(torch.float32)loss = FocalLoss(alpha=0.30)print(loss(inputs, targets))基本上,focal loss与二元交叉熵损失相同,只是增加了一个调节因子 α × ( 1 − p t ) γ \alpha\times(1-p_{t})^{\gamma} α×(1−pt)γ。在PyTorch中定义的损失函数与模型的定义方式相同,继承了nn.Module类。在forward函数中,我们首先对logits应用sigmoid来生成概率值§。接下来,我们使用logits计算二元交叉熵损失。Logits只是模型的最终原始输出,它代表在最后一个sigmoid或softmax层之前的输出。
pt是真实类别(正类)的概率,计算方式为p * targets + (1 - p) * (1 - targets),(1-p)负责处理负样本。利用gamma、pt和bce_loss计算损失。然而,请注意alpha部分未包含在损失计算中。alpha_t的计算方式与p_t类似。之后,这个alpha与计算出的损失相乘,得到平衡的损失值。记住,我们一批一批地传递图像和标签,因此我们需要对它们求平均,以获得整个批次损失的全面表示。
alpha的值可以这样计算:
alpha_t = self.alpha * targets + (1 - self.alpha) * (1 - targets)这里,提供了一个预定义的alpha值,targets是整数类标签。下面是一个如何确定alpha值的例子:
targets = torch.tensor([0.,0.,0.,0.,0.,1.,0.,0.,1.,0.])
alpha = 0.3
alpha_t = alpha * targets + (1 - alpha) * (1 - targets)
print(alpha_t) # 输出 -> tensor([0.7000, 0.7000, 0.7000, 0.7000, 0.7000, 0.3000, 0.7000, 0.7000, 0.3000,0.7000])上述,可以看到估计的alpha值是受0到1约束的逆类频率。
6. 总结
在深度学习的目标检测领域,损失函数扮演着至关重要的角色,它们不仅衡量模型预测与实际标注之间的差异,还引导模型参数的优化方向。以下是对YOLO损失函数的深入探讨和润色:
6.1 深度学习中的损失函数
损失函数是深度学习框架的核心,它通过计算预测输出与真实数据之间的差异来量化模型的准确性。这些函数是训练过程中优化算法的基础,帮助模型通过迭代调整参数来最小化预测误差。
6.2 凸与非凸损失函数
损失函数根据其几何特性可以分为凸和非凸两大类。凸损失函数,如均方误差或交叉熵损失,具有单一的全局最小值,这使得它们在优化时更为简单和稳定。相比之下,非凸损失函数可能拥有多个局部最小值,这为找到全局最优解带来了额外的挑战。
6.3 SIoU损失介绍
SIoU (Shape-Aware IoU) 损失是一种用于边界框回归的先进损失函数,它综合考虑了形状、距离和纵横比的对齐,以提升模型的收敛速度和预测准确性。SIoU损失通过结合角度成本、距离成本、形状成本和IoU成本,优化了边界框的定位精度。
6.4 目标检测中的Focal Loss
Focal Loss是为解决目标检测中的类别不平衡问题而设计的一种损失函数。它通过增加对难以分类样本的关注,同时减少对多数类样本的权重,从而有效地处理了数据集中的不平衡性。Focal Loss通过引入一个调节因子来改进传统的交叉熵损失,使得模型能够更加关注那些难以分类的样本。此外,Focal Loss还允许通过参数Alpha调整损失贡献,提供了灵活性以适应不同的训练需求。
6.5 用例
SIoU损失和Focal Loss在深度学习模型,尤其是在目标检测任务中,得到了广泛的应用。它们不仅提高了模型的性能,还解决了诸如类别不平衡和边界框定位不准确等常见问题。
在本文中,我们详细讨论了YOLO系列模型中使用的两种损失函数:SIoU损失和Focal损失。SIoU损失专注于边界框回归任务,通过考虑形状、距离和纵横比的不一致性,实现了更快的收敛和更高的推理准确性。Focal Loss则在处理类别不平衡问题时展现出其强大的能力,并在目标检测模型的训练中得到了广泛应用。
继这些损失函数之后,研究者们还引入了Varifocal Loss (VFL)和Distribution Focal Loss (DFL)等新型损失函数,它们分别与YOLOv6和YOLOv8模型集成,进一步推动了目标检测技术的发展。
这篇关于YOLO损失函数——SIoU和Focal Lossr损失函数解析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


