Transformer模型详解04-Encoder 结构

本文主要是介绍Transformer模型详解04-Encoder 结构，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

简介

Transformer 模型中的 Encoder 层主要负责将输入序列进行编码，将输入序列中的每个词或标记转换为其对应的向量表示，并且捕获输入序列中的语义和关系。

具体来说，Transformer Encoder 层的作用包括：

1. 词嵌入（Word Embedding）：将输入序列中的每个词或标记映射为其对应的词嵌入向量。这些词嵌入向量包含了词语的语义信息，并且可以在模型中进行学习。

2. 位置编码（Positional Encoding）：因为 Transformer 模型不包含任何关于序列顺序的信息，为了将位置信息引入模型，需要添加位置编码。位置编码是一种特殊的向量，用于表示输入序列中每个词的位置信息，以便模型能够区分不同位置的词。

3. 多头自注意力机制（Multi-Head Self-Attention）：自注意力机制允许模型在处理每个词时，同时考虑到输入序列中所有其他词之间的关系。多头自注意力机制通过将输入进行多次线性变换并计算多组注意力分数，从而允许模型在不同的表示子空间中学习到不同的语义信息。

4. 残差连接（Residual Connection）：为了减轻梯度消失和加速训练，Transformer Encoder 层使用了残差连接。残差连接允许模型直接学习到输入序列的增量变换，而不是完全替代原始输入。

5. 层归一化（Layer Normalization）：在残差连接后应用层归一化，有助于提高模型的训练稳定性，加快训练速度。

Transformer Encoder 层的主要作用是将输入序列转换为其对应的向量表示，并且捕获输入序列中的语义和位置信息，以便后续的模型能够更好地理解和处理输入序列。

前面我们已经详解了三个点，词嵌入（Word Embedding），位置编码（Positional Encoding），多头自注意力机制（Multi-Head Self-Attention），这里详解Encoder结构的其他部分。

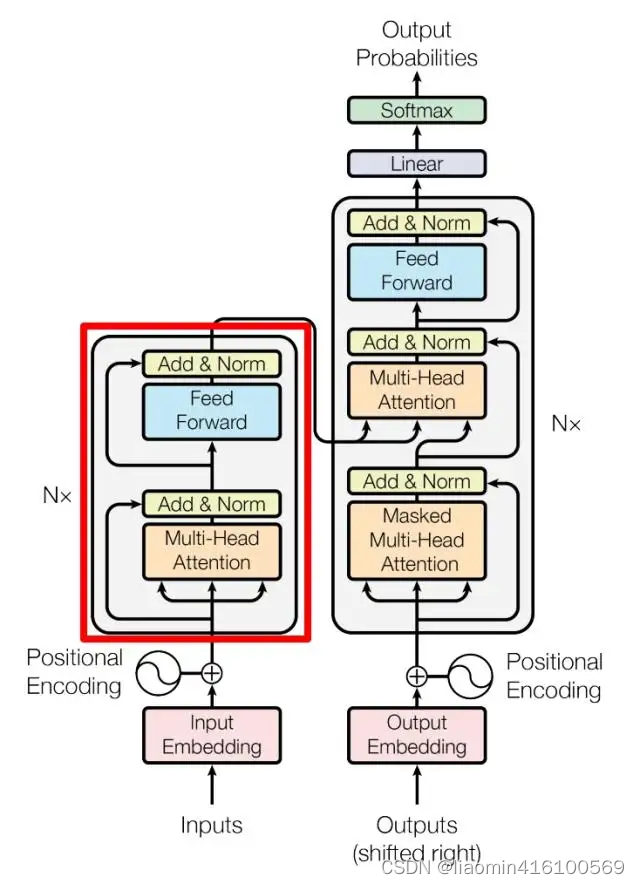
上图红色部分是 Transformer 的 Encoder block 结构，可以看到是由 Multi-Head Attention, Add & Norm, Feed Forward, Add & Norm 组成的。之前了解了 Multi-Head Attention 的计算过程，现在了解一下 Add & Norm 和 Feed Forward 部分。

基础知识

归一化

归一化是将数据转换为具有统一尺度的过程，常用于机器学习、数据挖掘和统计分析中。归一化可以确保不同特征或变量之间具有相似的数值范围，有助于提高模型的性能和收敛速度。

作用

让我用一个简单的例子来说明归一化的作用。

假设你有一个数据集，其中包含两个特征：年龄和收入。年龄的范围是 0 到 100 岁，而收入的范围是 1000 到 100000 美元。这两个特征的范围差异很大。

现在，你想要使用这些特征来训练一个机器学习模型，比如线性回归模型，来预测一个人是否会购买某种产品。由于特征的范围差异较大，这可能会导致某些问题：

收入的范围比年龄大得多，这可能会使得模型过度关注收入而忽略年龄，因为收入的变化可能会对预测产生更大的影响。
模型可能会受到数值范围的影响，而不是特征本身的重要性。
这时候，归一化就可以派上用场了。通过归一化，你可以将不同特征的值缩放到相似的范围内，从而消除数值范围差异带来的影响。比如，你可以将年龄和收入都缩放到 0 到 1 之间的范围内，或者使用其他归一化方法，如标准化 (standardization)。

通过归一化，你可以确保模型不会因为特征值的范围差异而偏向某个特定的特征，而是可以更平衡地利用所有的特征信息来进行预测。

常用归一化

下面是几种常用的归一化方式及其公式：

1. Min-Max 归一化：

Min-Max 归一化将数据线性映射到一个指定的范围内，通常是 [0, 1] 或 [-1, 1]。其公式如下：

$$[X_{\text{norm}}=\frac{X-X_{\text{min}}}{X_{\text{max}}-X_{\text{min}}}]$$

其中，$(X_{\text{norm}})$ 是归一化后的数据，(X) 是原始数据，$(X_{\text{min}})$ 和 $(X_{\text{max}})$分别是数据的最小值和最大值。

2. Z-Score 标准化：

Z-Score 标准化将数据转换为均值为 0，标准差为 1 的正态分布。其公式如下：

$$[X_{\text{norm}}=\frac{X-\mu }{\sigma }]$$

其中，$(X_{\text{norm}})$是归一化后的数据，$(X)$ 是原始数据，$\mu$是数据的均值，$(\sigma )$是数据的标准差。

3. Decimal Scaling 归一化：

Decimal Scaling 归一化将数据缩放到[-1,1]或者[0,1]的范围内，通过除以数据中的最大绝对值来实现。其公式如下：

$$[X_{\text{norm}}=\frac{X}{\max (|X|)}]$$

其中，$(X_{\text{norm}})$ 是归一化后的数据，$(X)$ 是原始数据，$(\max (|X|))$ 是数据中的最大绝对值。

4. Robust Scaling：

Robust Scaling 是一种针对离群值鲁棒的归一化方法，通过除以数据的四分位距（IQR）来缩放数据。其公式如下：

$$[X_{\text{norm}}=\frac{X-Q_1}{Q_3-Q_1}]$$

其中，$(X_{\text{norm}})$ 是归一化后的数据，$(X)$是原始数据，$(Q_1)$ 是数据的第一四分位数（25th percentile），$(Q_3)$ 是数据的第三四分位数（75th percentile）。

这些是常用的归一化方式，选择适合你的数据和模型的归一化方法可以提高模型的性能和稳定性。

残差连接

残差连接（Residual Connection）是一种在深度神经网络中用于解决梯度消失和梯度爆炸问题的技术。它通过将输入直接添加到神经网络的某些层的输出中，从而允许梯度直接通过残差路径传播，减轻了梯度消失的问题，加速了训练过程。

具体来说，假设我们有一个包含多个层的神经网络，每个层都由输入 $x$ 经过一些变换 $F(x)$得到输出 $H(x)$。传统的神经网络会直接将 $H(x)$ 作为下一层的输入，而残差连接则是将 $x$ 与 $H(x)$ 相加，即 $H(x)+x$，然后再输入到下一层。这样做可以使得网络学习到的变换是相对于输入的增量，而不是完全替代原始输入。

残差连接的作用包括：

1. 缓解梯度消失：通过保留原始输入的信息，使得梯度可以更容易地传播到较浅层，从而减轻了梯度消失问题。
2. 加速训练：残差连接可以使得神经网络更快地收敛，因为它减少了训练过程中的信息丢失。
3. 提高模型性能：残差连接使得神经网络可以更深，更复杂，从而能够更好地捕捉输入数据的特征和模式。

举个例子，考虑一个包含残差连接的深度残差网络（Residual Network，ResNet）。在这个网络中，每个残差块都由两个或多个卷积层组成，其中第一个卷积层产生特征图 $H(x)$，而第二个卷积层则对 $H(x)$ 进行进一步变换。然后，原始输入 $x$ 被添加到 $H(x)$ 上，得到 $F(x)=H(x)+x$。这样，输出 $F(x)$ 就包含了相对于输入 $x$ 的增量，网络可以更轻松地学习到残差部分，从而更有效地优化模型。

Add & Norm

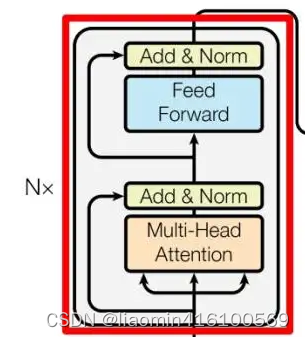
Add & Norm 层由 Add 和 Norm 两部分组成，其计算公式如下：

第一个Add&Norm中Add指 X+MultiHeadAttention(X)，是一种残差连接，通常用于解决多层网络训练的问题，可以让网络只关注当前差异的部分，在 ResNet 中经常用到：

Norm指 Layer Normalization，通常用于 RNN 结构，Layer Normalization 会将每一层神经元的输入都转成均值方差都一样的，这样可以加快收敛。

Feed Forward

Feed Forward 层比较简单，是一个两层的全连接层，第一层的激活函数为 Relu，第二层不使用激活函数，对应的公式如下。
$$\text{FFN}(x)=\text{ReLU}(x{W}_1+b_1)W_2+b_2$$
也就是：

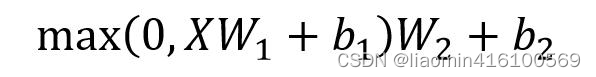
在这个公式中：

• $(X)$ 是输入的隐藏表示，维度为 $(d_{\text{model}})$，是Add&Norm输出；
• $(W_1)$ 和 $(W_2)$ 是权重矩阵，分别用于第一层和第二层的线性变换，维度分别为 $(d_{\text{model}}\times d_{\text{ff}})$ 和 $(d_{\text{ff}}\times d_{\text{model}})$；
• $(b_1)$ 和 $(b_2)$ 是偏置项；
• $(\text{ReLU})$ 表示修正线性单元，是一种非线性激活函数，用于引入模型的非线性性。

Feed Forward 最终得到的输出矩阵的维度与X一致。

Feed Forward 层在深度学习模型中具有重要意义，它主要有以下几个方面的作用：

1. 特征变换与组合： Feed Forward 层通过线性变换和非线性激活函数将输入数据进行特征变换和组合，使得模型能够学习到更高级、更复杂的特征表示。这有助于模型更好地理解数据的内在结构和规律。

2. 引入非线性： 非线性激活函数（如 ReLU、sigmoid、tanh 等）可以引入非线性变换，从而使得模型能够学习到非线性关系，提高模型的表达能力。如果没有非线性变换，多个线性变换的组合仍然只会得到线性变换，模型的表达能力将受到限制。

3. 增加模型的深度： Feed Forward 层通常是深度神经网络中的一个组成部分，通过堆叠多个 Feed Forward 层可以构建深度模型。深度模型能够学习到更多层次、更抽象的特征表示，从而提高模型的性能和泛化能力。

4. 提高模型的泛化能力： Feed Forward 层通过特征变换和非线性变换有助于模型学习到数据的高级抽象表示，这有助于提高模型对新样本的泛化能力，使得模型更好地适应未见过的数据。

组成 Encoder

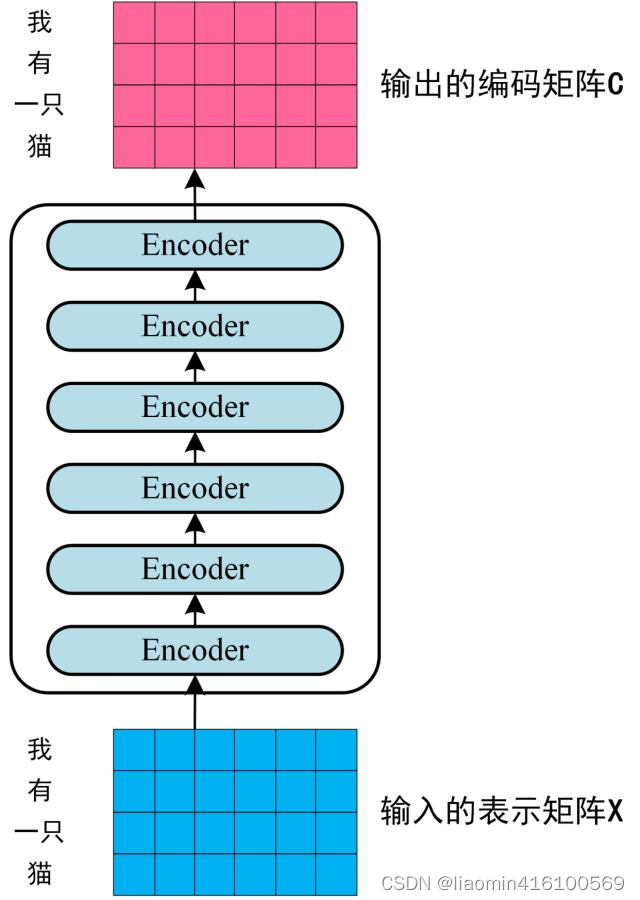
通过上面描述的 Multi-Head Attention, Feed Forward, Add & Norm 就可以构造出一个 Encoder block，Encoder block 接收输入矩阵$X_{(}n\ast d)$, 并输出一个矩阵$O_{(}n\ast d)$,通过多个 Encoder block 叠加就可以组成 Encoder。
第一个 Encoder block 的输入为句子单词的表示向量矩阵，后续 Encoder block 的输入是前一个 Encoder block 的输出，最后一个 Encoder block 输出的矩阵就是编码信息矩阵 C，这一矩阵后续会用到 Decoder 中。

代码实现

import torch
import torch.nn as nn
import torch.nn.functional as Fclass TransformerEncoderLayer(nn.Module):def __init__(self, d_model, n_heads, d_ff, dropout=0.1):super(TransformerEncoderLayer, self).__init__()self.self_attn = nn.MultiheadAttention(d_model, n_heads, dropout=dropout)self.linear1 = nn.Linear(d_model, d_ff)self.linear2 = nn.Linear(d_ff, d_model)self.dropout = nn.Dropout(dropout)self.norm1 = nn.LayerNorm(d_model)self.norm2 = nn.LayerNorm(d_model)def forward(self, src, src_mask=None):# Multi-head self-attentionsrc2 = self.self_attn(src, src, src, attn_mask=src_mask)[0]src = src + self.dropout(src2)src = self.norm1(src)# Feed Forward Layersrc2 = self.linear2(F.relu(self.linear1(src)))src = src + self.dropout(src2)src = self.norm2(src)return srcclass TransformerEncoder(nn.Module):def __init__(self, num_layers, d_model, n_heads, d_ff, dropout=0.1):super(TransformerEncoder, self).__init__()self.layers = nn.ModuleList([TransformerEncoderLayer(d_model, n_heads, d_ff, dropout) for _ in range(num_layers)])def forward(self, src, src_mask=None):for layer in self.layers:src = layer(src, src_mask)return src

这篇关于Transformer模型详解04-Encoder 结构的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---