本文主要是介绍算法-卡尔曼滤波之卡尔曼滤波的第二个方程：预测方程（状态外推方程），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
在上一节中，使用了静态模型，我们推导出了卡尔曼滤波的状态更新方程，但是在实际情况下，系统都是动态，预测阶段，前后时刻的状态是改变的，此时我们引入预测方程，也叫状态外推方程；
同样的我们通过一个例子来分析，在开始为什么要选择卡尔曼滤波时，提出了一个例子；
在一维空间内使用雷达来追踪匀速飞行的飞行器，此时系统状态为飞行器的航程，速度是相对于时间的变化率，也就是距离的导数；
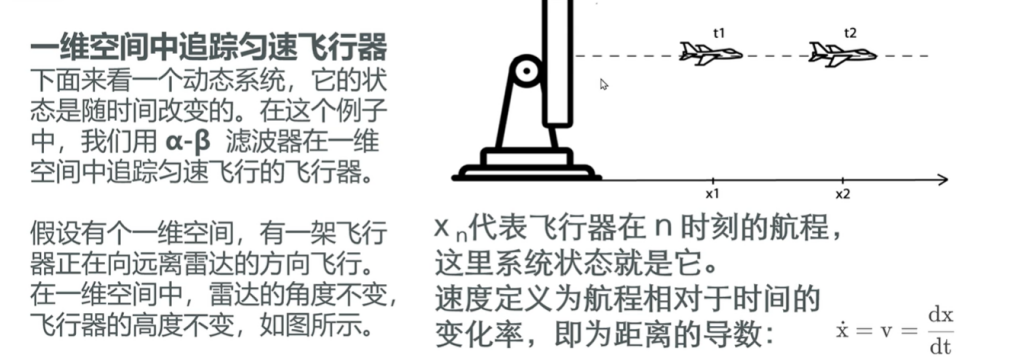
通过分析飞行器的一维物理模型，可以得到，速度恒定时，航程等于当前时刻的的航程加上时间变化*速度（距离的导数） ；
得到的动态模型，我们称为状态外推方程或者预测方程；
具体化这个例子：
对于存在问题，我们分析得到两种情况：一个是雷达的误差，另外就是飞行器速度改变了；
假设雷达的精度是20m，此时的误差更可能是由于飞行器速度发生了改变，那么此时我们更信任雷达的测试结果，所以我们将系数调高（当系数β=1时，估计值结果=测量值）；
假设雷达的精度是150m，此时的误差更可能是由于雷达误差结果，那么此时我们更信任飞机速度变化，所以我们将系数调低（当系数β=0时，估计值结果=先验估计值）；
具体流程：根据分析，我们设置权重因子，开始第0次迭代，首先依然是初始化，输入估计值，与上一个例子不同是，此时我们是动态模型，预测后，先验估计值与输入值是不同的；
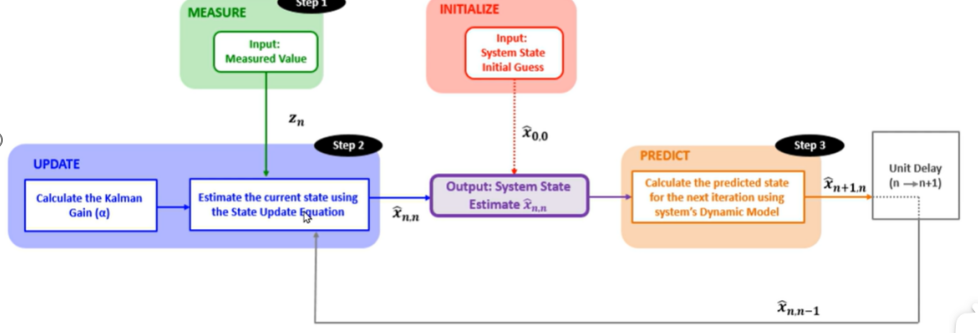
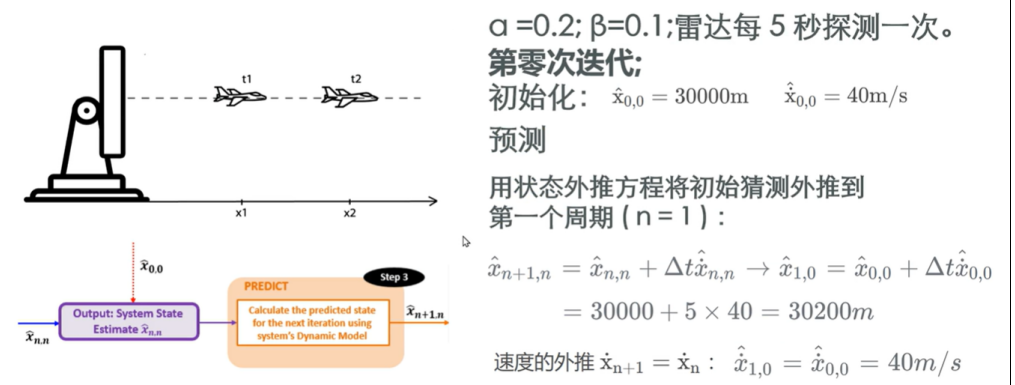
将预测的结果作为输入给到状态更新方程，同时输入测量值，通过状态更新方程计算当前估计值；
继续预测下一刻的先验估计值；
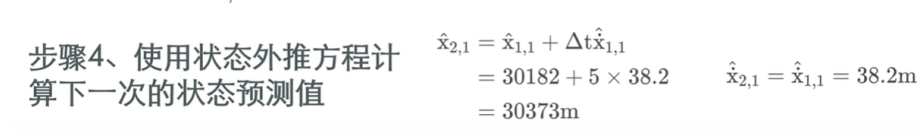
不断迭代:最终我们得到结果
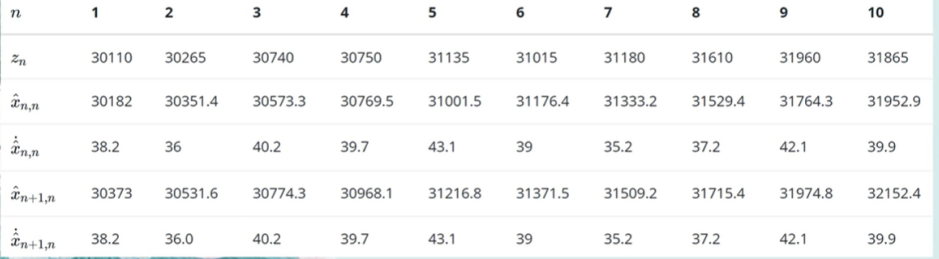
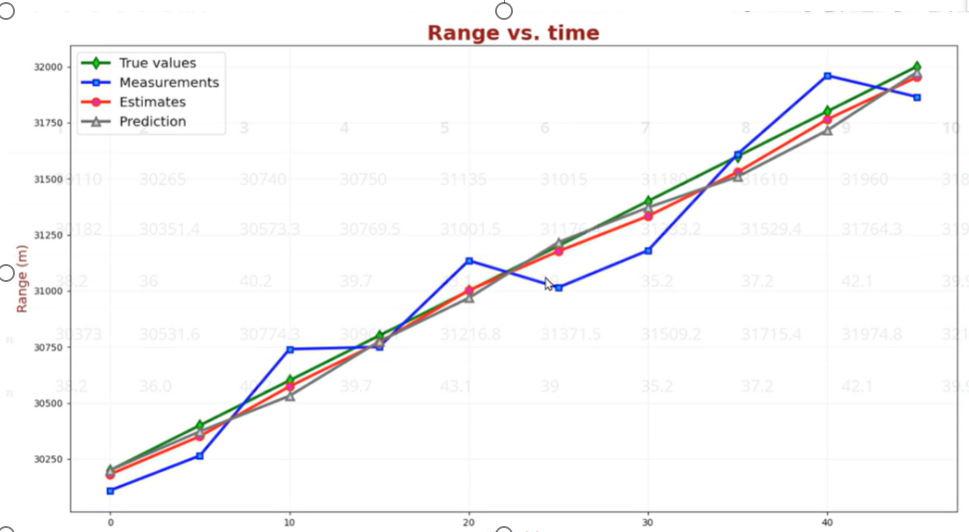
我们可以看出，可以看到估计算法对估计结果有平滑作用，并且估计结果趋近真实值。
尝试改变权重因子：
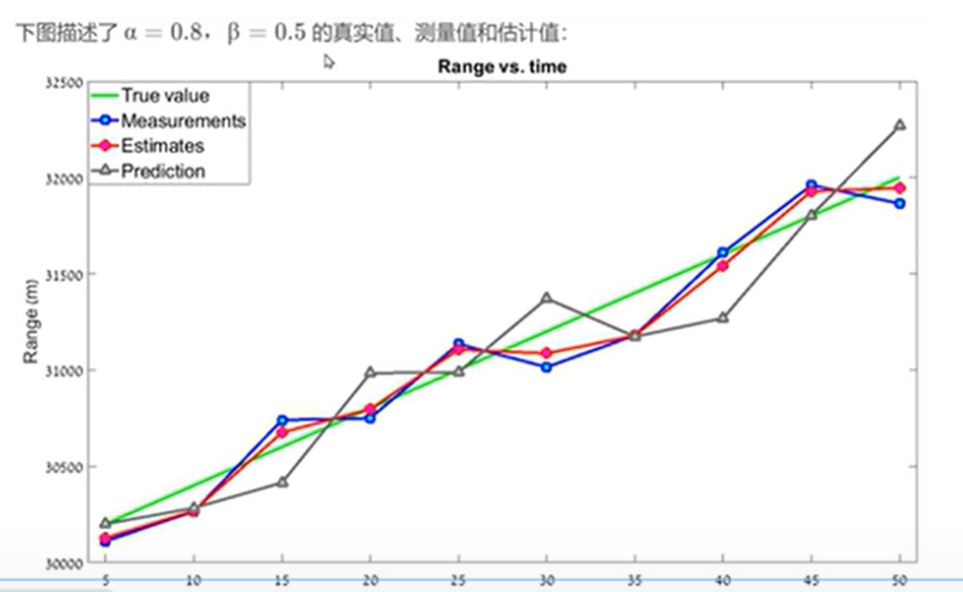
结果并不理，所以滤波器系数的选择是至关重要的；
滤波器系数的选择：
对于这个案例，系统状态为航程情况下，动态改变的除了速度还可能有加速度，例如现在来一架战斗机，它先以50m/s 的恒定速度飞行 15 秒然后以 8 m/s2 的加速度匀加速飞行 35秒。入图显示了目标航程、速度、加速度随时间的变化。此时α-β两个系数将不能满足我们的需求，依然使用该滤波器，分析：
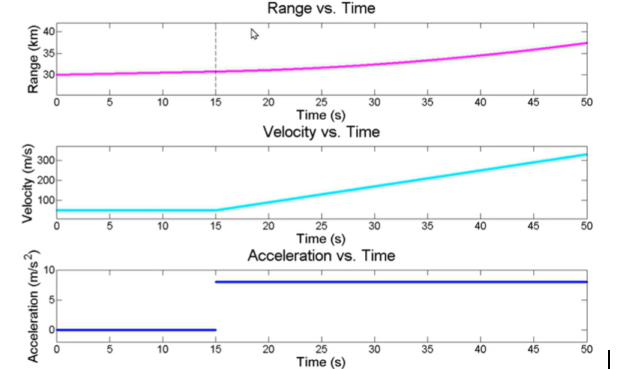
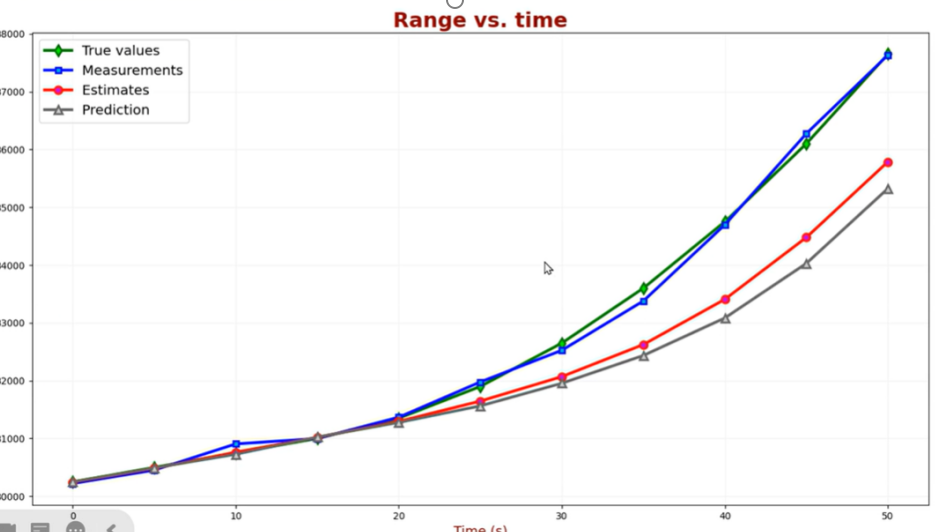
会发现，误差非常大：
现在使用α-β-Γ滤波器来追踪：
根据动力学分析，此时的系统状态外推方程：
最终得到结果：航程的拟合还是不错的；
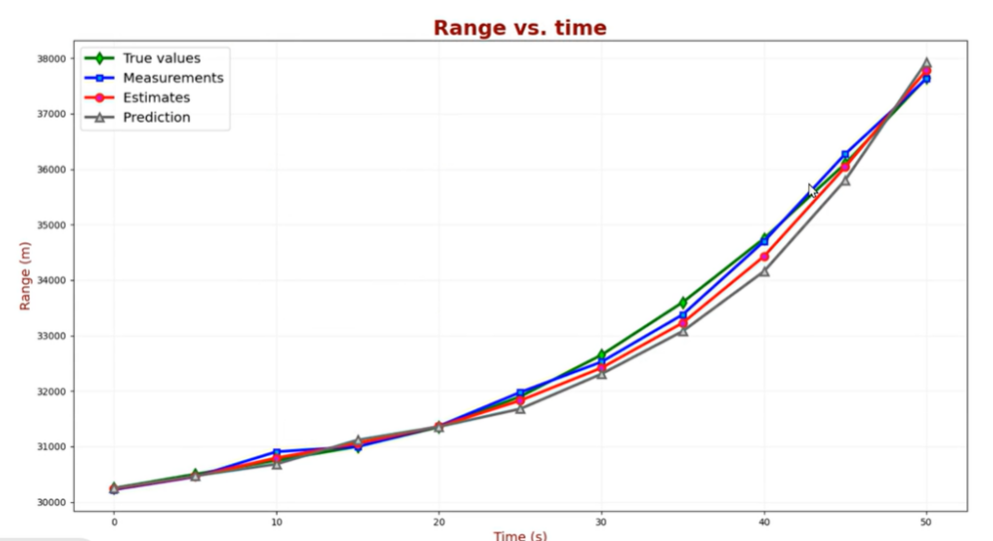
但是速度和加速度的拟合效果并不好：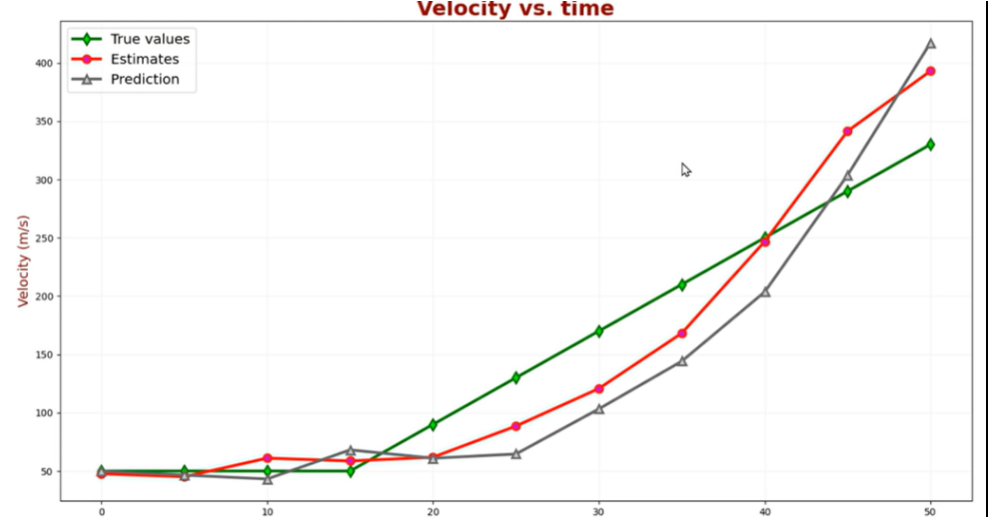
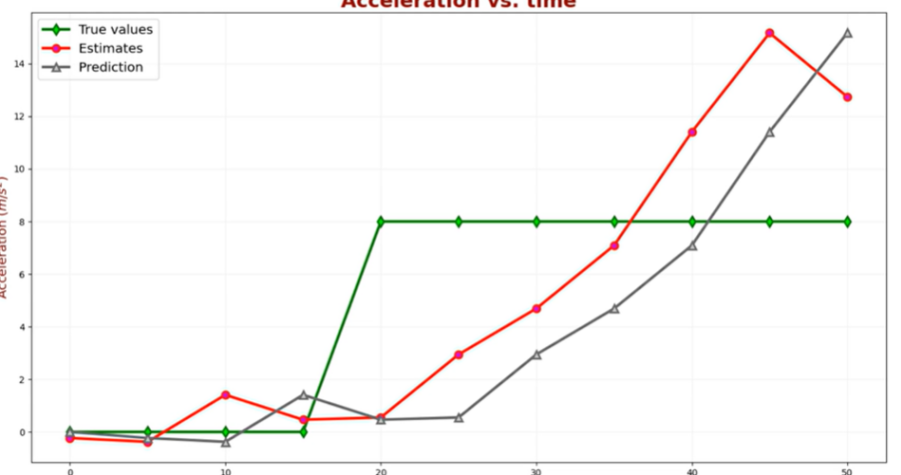
卡尔曼滤波器就可以处理动态情况下的问题；
总结:
卡尔曼滤波的第一个方程：通过先验估计值和对残差的权重求和得到当前估计值；
卡尔曼滤波的第二个方程：通过动态模型，得到状态外推方程，去求得先验估计值；
这篇关于算法-卡尔曼滤波之卡尔曼滤波的第二个方程：预测方程（状态外推方程）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
