本文主要是介绍动态规划 解TSP旅行商问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
原文地址: http://blog.csdn.net/gfaiswl/article/details/4749713
1.问题定义
TSP问题(旅行商问题)是指旅行家要旅行n个城市,要求各个城市经历且仅经历一次然后回到出发城市,并要求所走的路程最短。
假设现在有四个城市,0,1,2,3,他们之间的代价如图一,可以存成二维表的形式
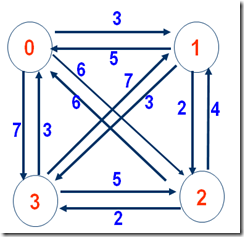
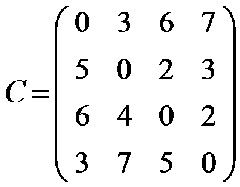
图一
现在要从城市0出发,最后又回到0,期间1,2,3都必须并且只能经过一次,使代价最小。
2.动态规划可行性
设s, s1, s2, …, sp, s是从s出发的一条路径长度最短的简单回路,假设从s到下一个城市s1已经求出,则问题转化为求从s1到s的最短路径,显然s1, s2, …, sp, s一定构成一条从s1到s的最短路径,所以TSP问题是构成最优子结构性质的,用动态规划来求解也是合理的。
3.推导动态规划方程
假设从顶点s出发,令d(i, V’)表示从顶点i出发经过V’(是一个点的集合)中各个顶点一次且仅一次,最后回到出发点s的最短路径长度。
推导:(分情况来讨论)
①当V’为空集,那么d(i, V’),表示从i不经过任何点就回到s了,如上图的 城市3->城市0(0为起点城市)。此时d(i, V’)=Cis(就是 城市i 到 城市s 的距离)、
②如果V’不为空,那么就是对子问题的最优求解。你必须在V’这个城市集合中,尝试每一个,并求出最优解。
d(i, V’)=min{Cik + d(k, V’-{k})}
注:Cik表示你选择的城市和城市i的距离,d(k, V’-{k})是一个子问题。
综上所述,TSP问题的动态规划方程就出来了:
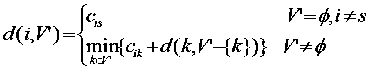
4.实例分析
现在对问题定义中的例子来说明TSP的求解过程。(假设出发城市是 0城市)
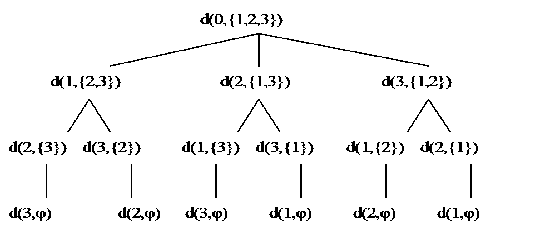
①我们要求的最终结果是d(0,{1,2,3}),它表示,从城市0开始,经过{1,2,3}之中的城市并且只有一次,求出最短路径.
②d(0,{1,2,3})是不能一下子求出来的,那么他的值是怎么得出的呢?看上图的第二层,第二层表明了d(0,{1,2,3})所需依赖的值。那么得出:
d(0,{1,2,3})=min {
C01+d(1,{2,3})
C02+d{2,{1,3}}
C03+d{3,{1,2}}
}
③d(1,{2,3}),d(2,{1,3}),d(3,{1,2})同样也不是一步就能求出来的,它们的解一样需要有依赖,就比如说d(1,{2,3})
d(1,{2,3})=min{
C12+d(2,{3})
C13+d(3,{2})
}
d(2,{1,3}),d(3,{1,2})同样需要这么求。
④按照上面的思路,只有最后一层的,当当V’为空集时,Cis的值才可以求,它的值是直接从
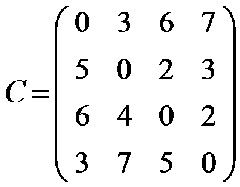
这张表里求得的。
5.编程思路
将d(i, V’)转换成二维表,d[i][j]
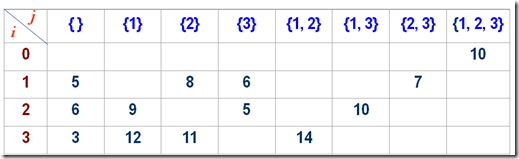
在程序中模拟填表的过程,主要要考虑到j这个参数的表示,它要代表一个集合,可以用二维数组来表示。
6.源代码
注:由于本人水平有限,并且主要在这里是体现思路,所以程序并不是很完善,代码质量也不高,很地方可以写得通用一些,所以这里只是提供一个参考,程序的进一步完善,由读者自由发挥。
#include
#include
int IsIncluded(int x,int array[3])//x是否包含在数组中
{
if((array[0] != x) && (array[1] != x) && (array[2] != x))
return 0;
return 1;
}
int Left(int k,int array[3],int V[8][3])//实现V'-{k} 的下标检索
{
int i = 0,index = 0,array_0_count = 0,array_1_count = 0,array_2_count = 0,array_3_count = 0;
int V_0_count = 0,V_1_count = 0,V_2_count = 0,V_3_count = 0;
int temp[3];
for(i = 0; i < 3; i++)
temp[i] = array[i];
for(i = 0; i < 3; i++)
if(temp[i] == k)
temp[i] = 0; //相当于去掉k这个城市
for(i = 0; i < 3; i++)
{
if(temp[i] == 0)
array_0_count++;
else if(temp[i] == 1)
array_1_count++;
else if(temp[i] == 2)
array_2_count++;
else
array_3_count++;
}
for(index = 0; index < 8; index++)
{
for(i=0; i < 3; i++)
{
if(V[index][i] == 0)
V_0_count++;
else if(V[index][i] == 1)
V_1_count++;
else if(V[index][i] == 2)
V_2_count++;
else
V_3_count++;
}
if((array_0_count == V_0_count) && (array_1_count == V_1_count)
&& (array_2_count == V_2_count) && (array_3_count == V_3_count))
return index;
V_0_count = 0;
V_1_count = 0;
V_2_count = 0;
V_3_count = 0;
}
return 0;
}
void TSP(int d[4][8],int c[4][4],int V[8][3],int n)
{
int i = 0,j = 0,k = 0;
for(i = 1; i < n; i++)//V'为空时,给赋值,
d[i][0] = c[i][0];
for(j = 1; j < 7; j++)//按列遍历不同集合,{1},{2},{3},{1,2},{1,3}.....
{
for(i = 1; i < n; i++)//遍历城市1,2,3
{
if( !IsIncluded(i,V[j]) )//i必须不在集合中,否则就属于经过两次,不符合题意
{
for(k = 0; k < 3; k++)//分别试探集合中的每一点,取最小值
{
if((V[j][k] != 0) && ((c[i][V[j][k]] + d[V[j][k]][Left(V[j][k],V[j],V)]) < d[i][j]))
d[i][j] = c[i][V[j][k]] + d[V[j][k]][Left(V[j][k],V[j],V)];
}
}
}//end of for(i = 1; i < n; i++)//遍历城市1,2,3
}//end of for(j = 1; j < ((int)pow(2,n)-1); j++)
for(k = 0; k < 3; k++)//分别试探下一步为集合中的任何一点,取最小值
{
if((V[7][k] != 0) && (c[0][V[7][k]] + d[V[7][k]][Left(V[7][k],V[7],V)]) < d[0][7])
d[0][7] = c[0][V[7][k]] + d[V[7][k]][Left(V[7][k],V[7],V)];
}
}
void main()
{
int V[8][3]=
{
0,0,0,
0,0,1,
0,0,2,
0,0,3,
0,1,2,
0,1,3,
0,2,3,
1,2,3
};
int c[4][4]=
{
0,3,6,7,
5,0,2,3,
6,4,0,2,
3,7,5,0
};
int d[4][8]={0},i=0,j=0;
for(i=0; i<4; i++)
for(j=0; j<8; j++)
d[i][j]=1000; //假设1000为无穷大
TSP(d,c,V,4);
printf("The least road is:%d/n",d[0][7]);
}
这篇关于动态规划 解TSP旅行商问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









