【随想录】Day46—第九章 动态规划part08

本文主要是介绍【随想录】Day46—第九章 动态规划part08，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

题目1: 139. 单词拆分

• 题目链接：139. 单词拆分

---

1- 思路

目标

• 根据字符串 String s 和 List<String> wordDict 来判断是否能通过 wordDict 组成 s

动规五部曲

• 1. 确定 dp 数组含义
  • 定义：根据字符串 s 的长度定义 dp[i] ——> 最终返回 dp[s.length()]
  • 含义：长度为 s 的字符串，是否能由数组 wordDict 组成
• 2. 确定递推公式
  • dp[i] 是 true 还是 false 依赖于其前面长度为 j 的字符串 dp[j]
  • 如果 dp[j] = true 且 ，i-j 为wordDict 中长度的单词 ——> 则 dp[i] = true
• 3. dp 数组初始化
  • dp[0] = true ，长度为 0 为了 dp 数组的推导
  • 非 0 下标的 dp 数组初始化为 false
• 4. 遍历顺序（所求为组合，因此需要先遍历背包再遍历物品）
  • 装满背包是对字符串的顺序是有要求的，因此本题目相当于求 排列问题 ——> 先遍历背包，再遍历物品
  • ① 先遍历背包 for(int i = 1 ; i <= s.length() ; i++)
  • ② 再遍历物品 for(int j = 0; j < i ; j++)
    • 此时需要对 i 到 j 中的字符串进行一个截取 ——> String str = s.subString(j,i-j)
  • 遍历内部逻辑：
    • 如果 dp[j] = true 且 ，i-j 为wordDict 中长度的单词 ——> 则 dp[i] = true
    • dp[j] = true

---

2- 题解

⭐单词拆分——题解思路

class Solution {public boolean wordBreak(String s, List<String> wordDict) {// 背包 s// 商品 wordDictHashSet<String> set = new HashSet<>(wordDict);// 1. 定义 dp 数组确定含义boolean[] dp = new boolean[s.length()+1];// 2. 确定递推公式// 如果 dp[j] = true 且  的子串在 wordDict 中 则 dp[j] = true// 3. 初始化dp[0] = true;// 4. 遍历顺序，排列问题// 先背包 后物品for(int i = 1 ; i <= s.length();i++){for(int j = 0 ; j <i && !dp[i];j++){if(set.contains(s.substring(j,i)) && dp[j]){dp[i] = true;}}}return dp[s.length()];}
}

---

题目2: 完全背包

• LeetCode无原题

---

题目3: 背包问题总结

• 主要常见的背包问题有 ①01背包、②完全背包、③多重背包

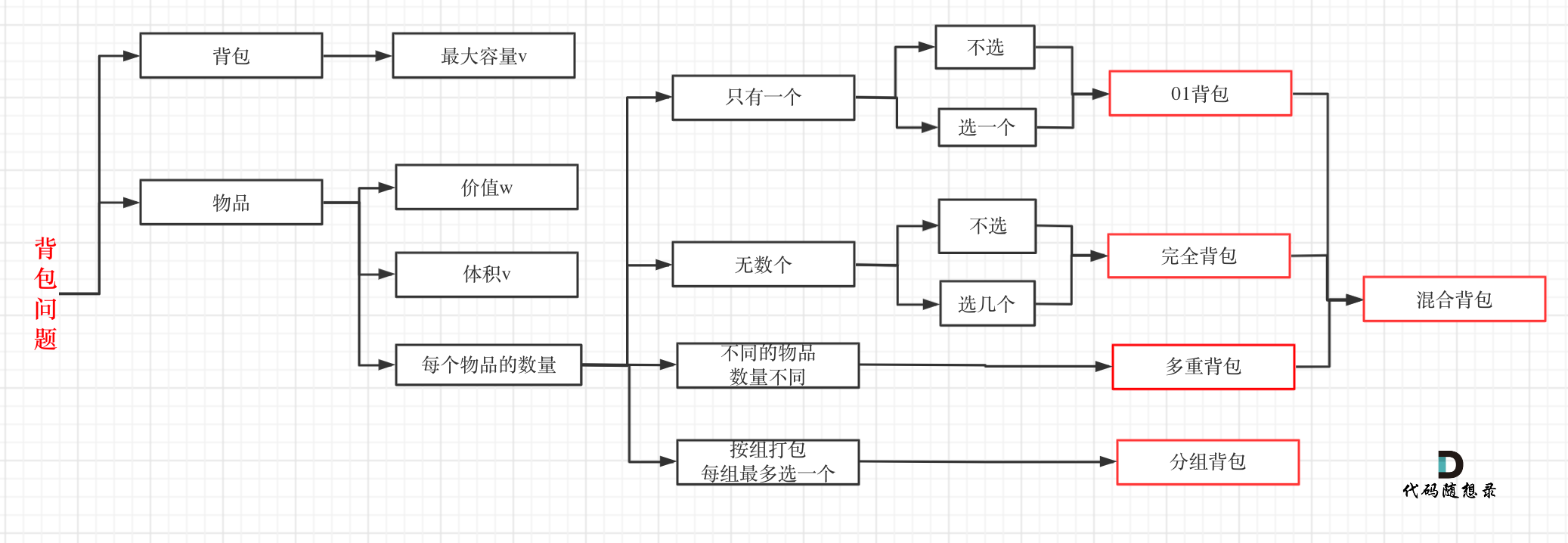
总结

这篇背包问题总结篇是对背包问题的高度概括，讲最关键的两部：递推公式和遍历顺序，结合力扣上的题目全都抽象出来了。
而且每一个点，我都给出了对应的力扣题目。
最后如果你想了解多重背包，可以看这篇动态规划：关于多重背包，你该了解这些！(opens new window)，力扣上还没有多重背包的题目，也不是面试考察的重点。
如果把我本篇总结出来的内容都掌握的话，可以说对背包问题理解的就很深刻了，用来对付面试中的背包问题绰绰有余！
背包问题总结：

---

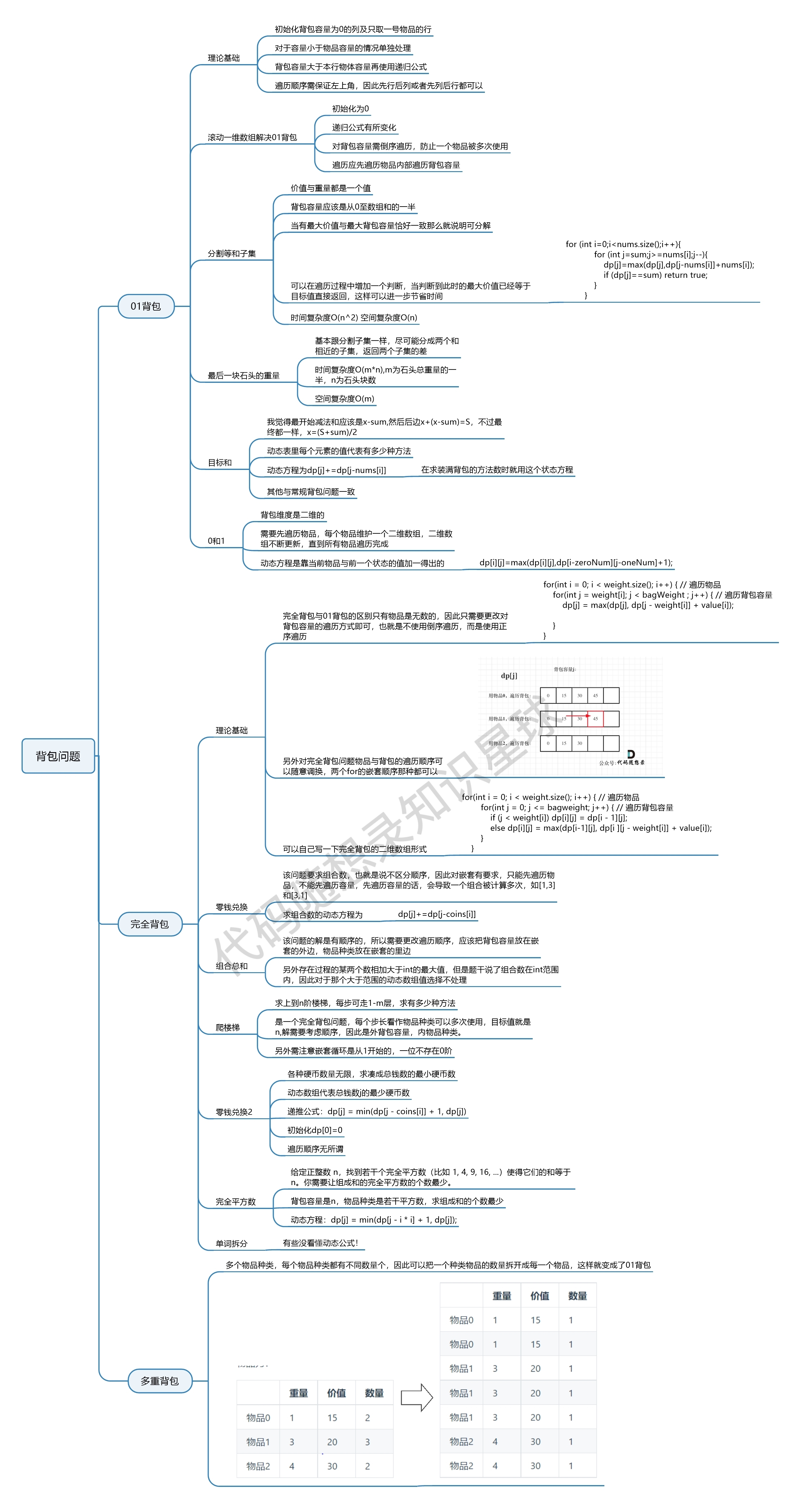
这篇关于【随想录】Day46—第九章 动态规划part08的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---