何为小波变换？

本文主要是介绍何为小波变换？，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、数学基础

小波 变换脱胎于傅里叶变换，但是有着傅里叶变换的优点。

1.1 点乘（内积）

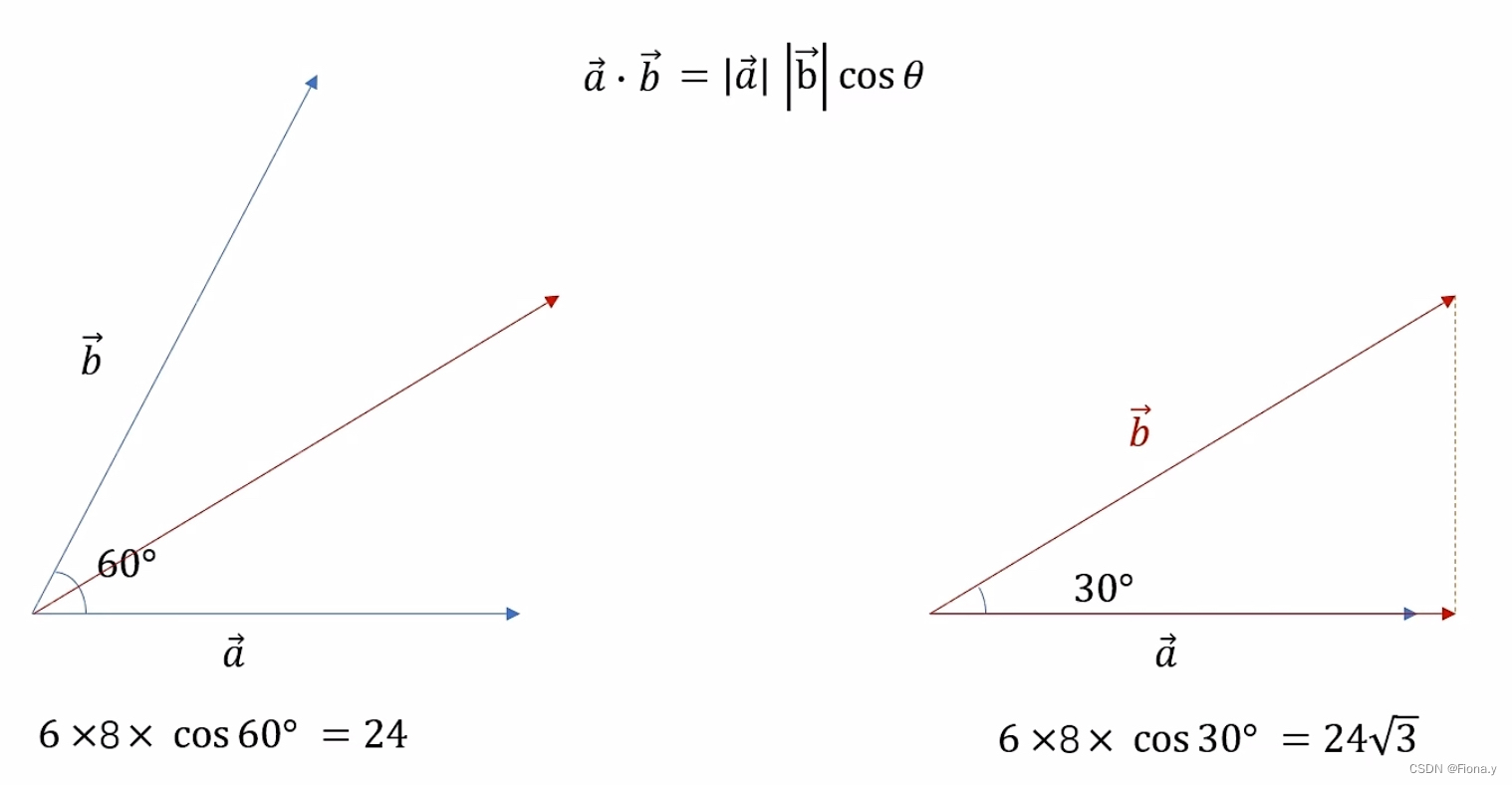
a = 6; b = 8;

点乘的作用：衡量两个事物的相似度（Similarity）

夹角变小，点乘结果变大，结果越大相似度越高

1.2 观察者

将向量a看作是一个观察者，观察向量b与自己有多像；

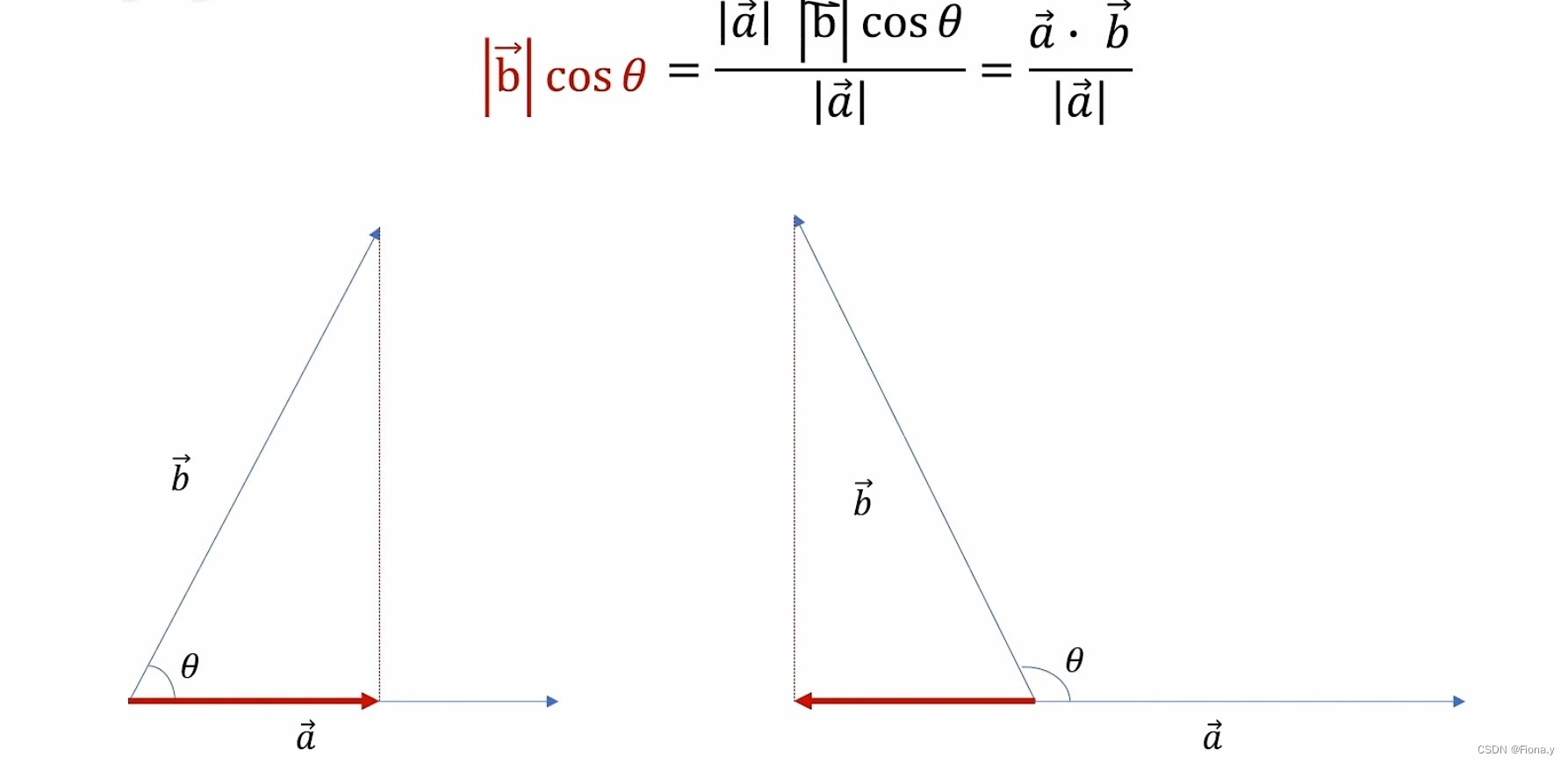
只要向量b在向量a上有投影，说明都具有一定的相似度，但是只要a与b垂直，那么就不相似，即使方向相反，也是相似的。

二、观察者眼中的向量分解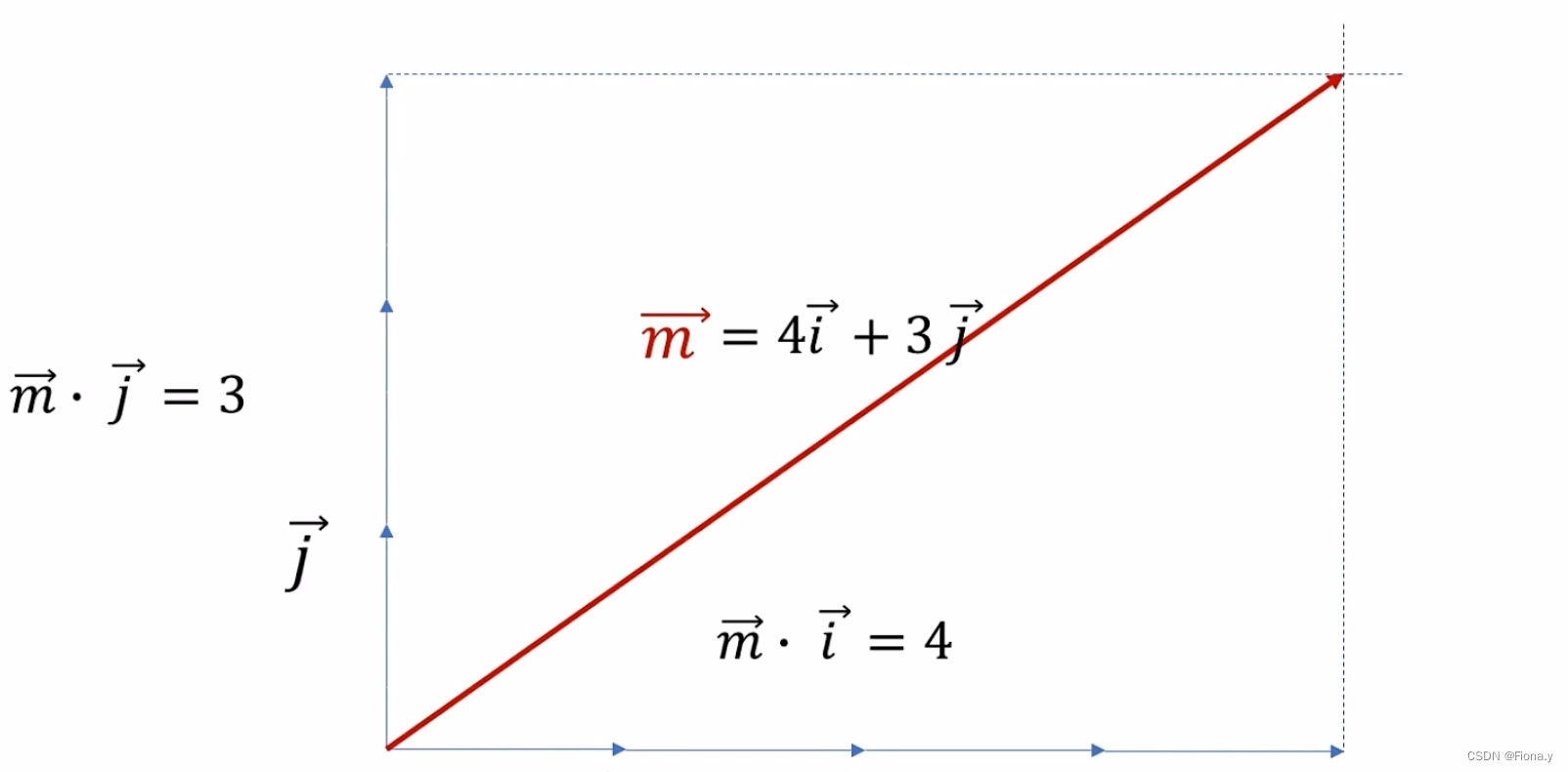

向量i与向量m的相似度更高

向量i与向量j的长度均为1，此为归一化操作。

为什么要归一化：

1、保障基准一致

2、保障各个观察者的能量一致

3、方便后续数据处理

向量如何归一化：向量除以自己的模长即可。即单位向量

4与3均是投影系数，即，不同方向上，不同观察者观察到的目标的量值是多少

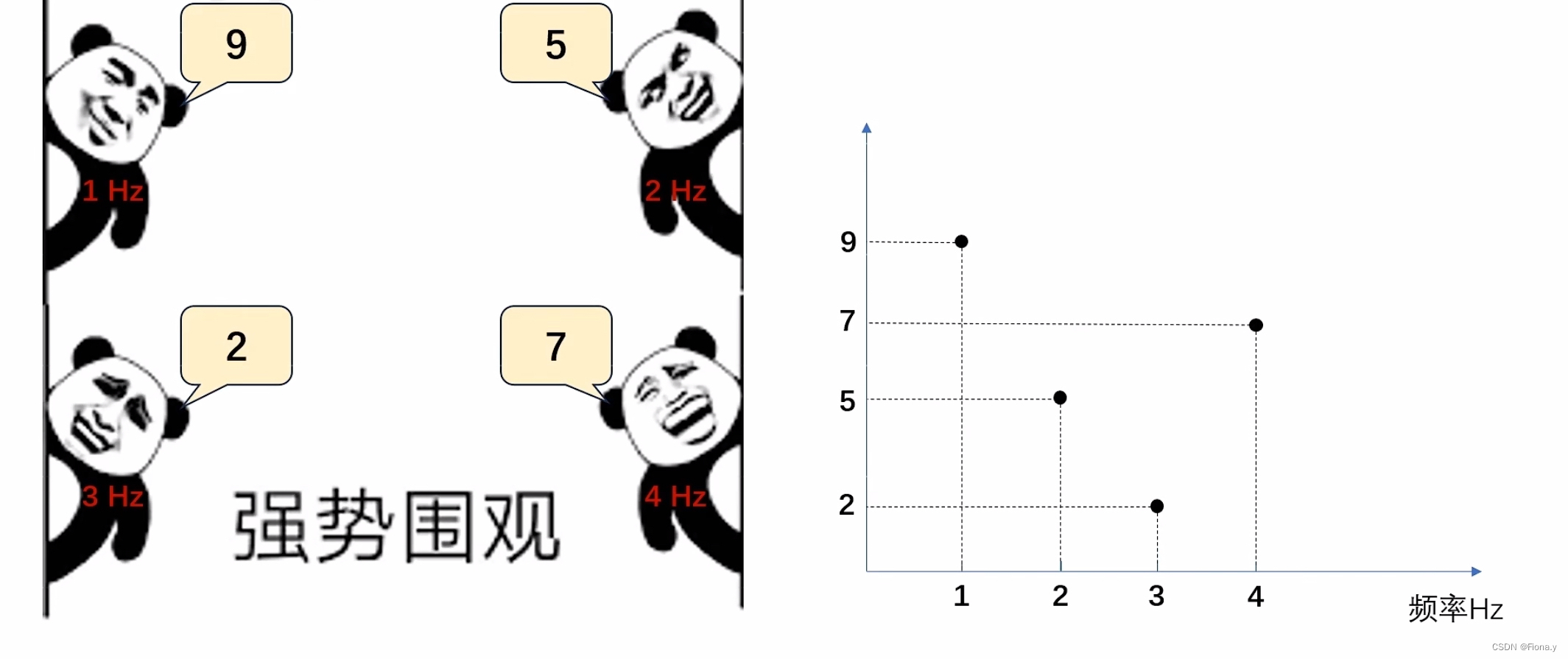
每个人看一眼，总结出来得到全貌4i+3j

点乘观察者是了解未知事物的手段

三、在直角坐标系中了解点乘

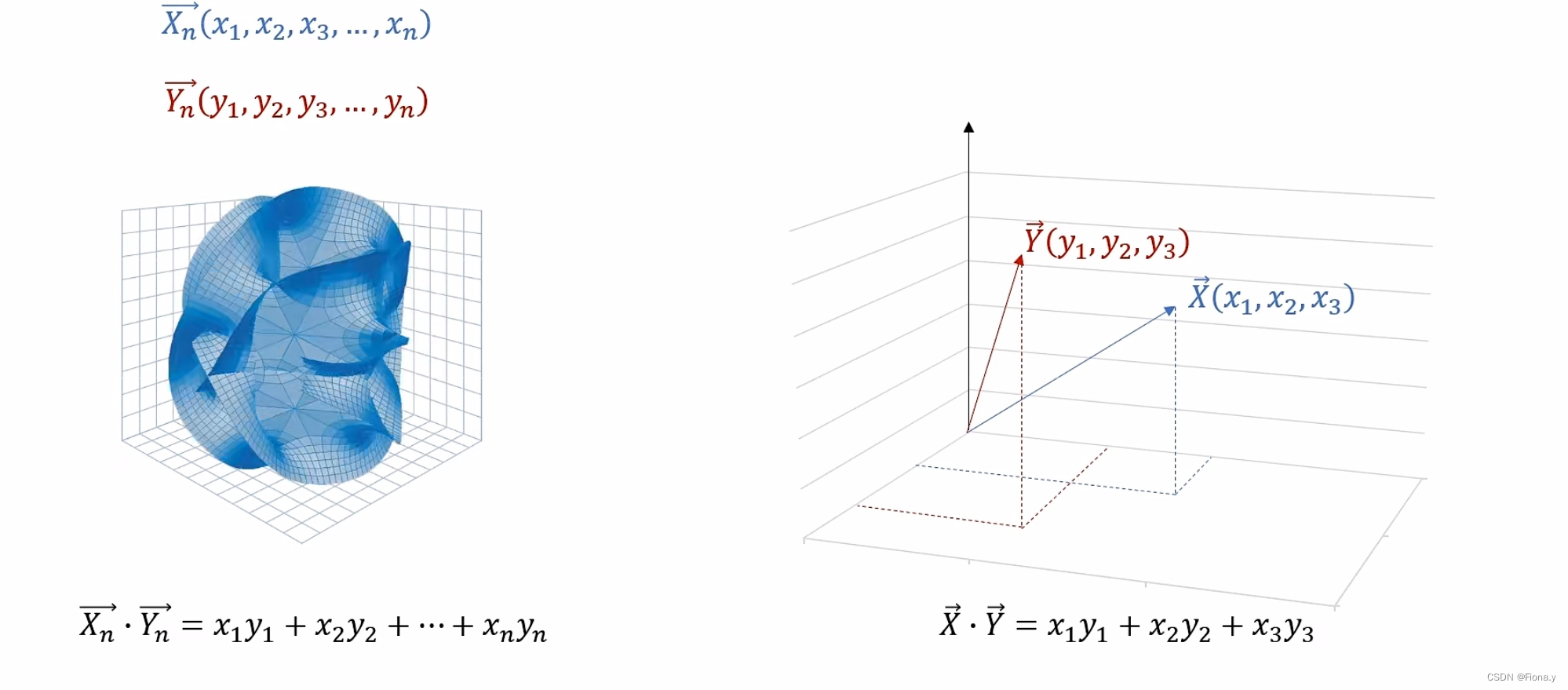
点乘在坐标系中，就是对应坐标相乘相加。

将xn的值与yn的值对应撒到直角坐标系中，会得到离散的值，当n趋于无穷的时候，那么就变成了连续的X(t)与Y(t)

在离散的值中，是对应x与y的值相乘后相加，在连续函数中，则相乘后积分。

当积分结果为0时候，相似度为0；无论结果是正或者是负值，都具有相似度。

四、傅里叶级数

傅里叶级数是由一系列的sin与cos作为基。这些基都是一系列的观察者（通过不同频率来区分）。

观察者与目标函数的相似度，越相似，占比越大。确定他们的相似度，通过点乘再积分。

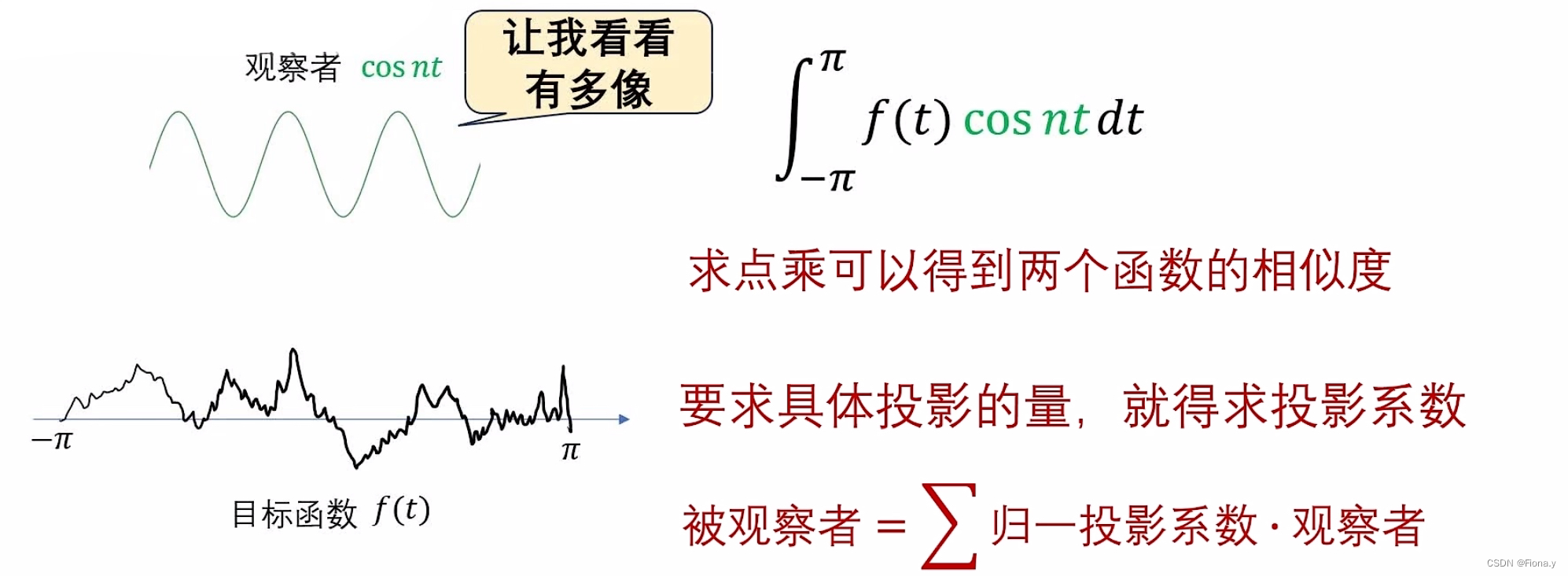
被观察者 = 诡异投影系数 ·观察者

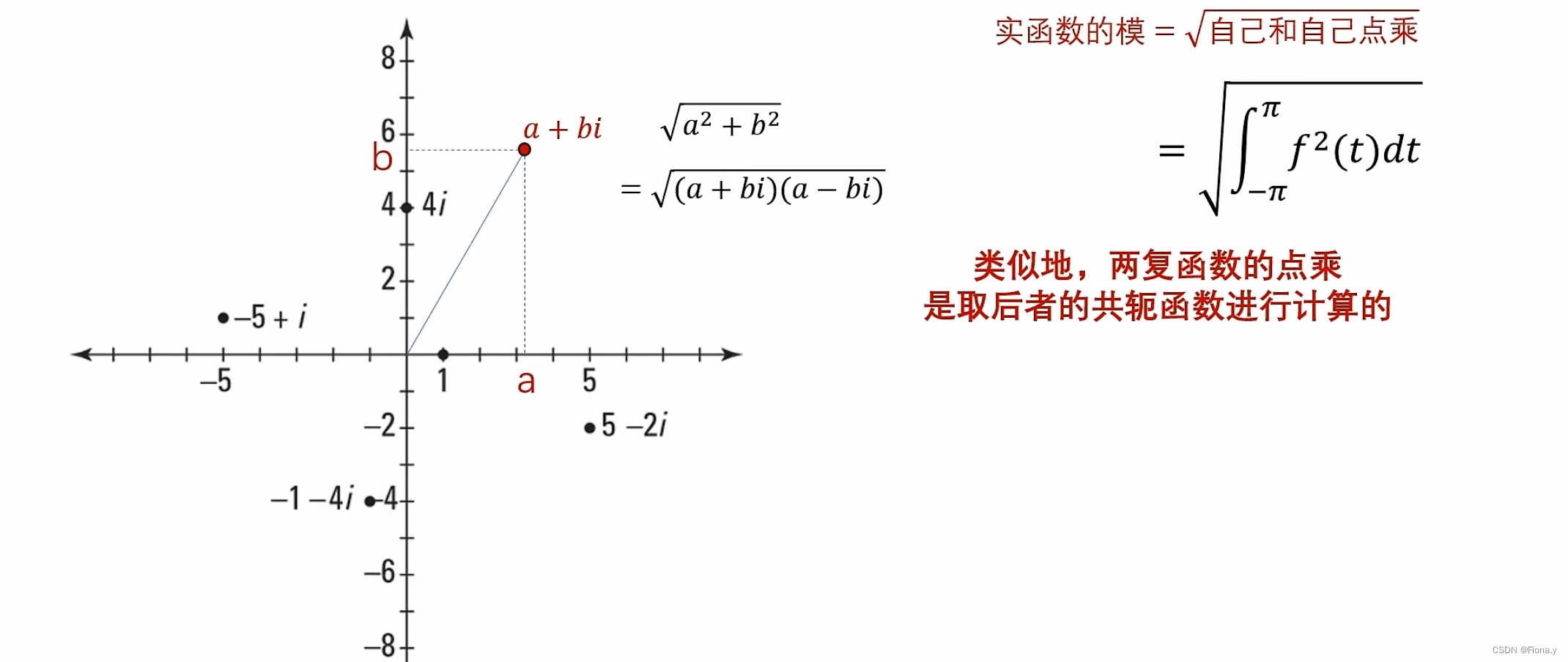
对于向量的归一化，就是求模长 = 自己和自己点乘

连续函数的模长  =  f(t)^2 dt

模长对于一个函数称之为二范数（Euclidean morn）

归一投影系数 = 目标·观察者/|观察者模长|^2

即An的式子

五、负指数形式的傅里叶变换

        与上述相似，只是观察者由之前的cos函数变成了e^jwt，观察域从实数域拓展到了带虚数的复数域。w是角频率，越大越快。

查看相似度：

存在的问题：

观察者在整条时间轴一起看，就算只有一部分相似度高，就说具有相似性质。

六、观察者的改造

局域化：乘以衰减系数，则观察者在时间轴上不再是无穷无尽的。

观察者巡逻：

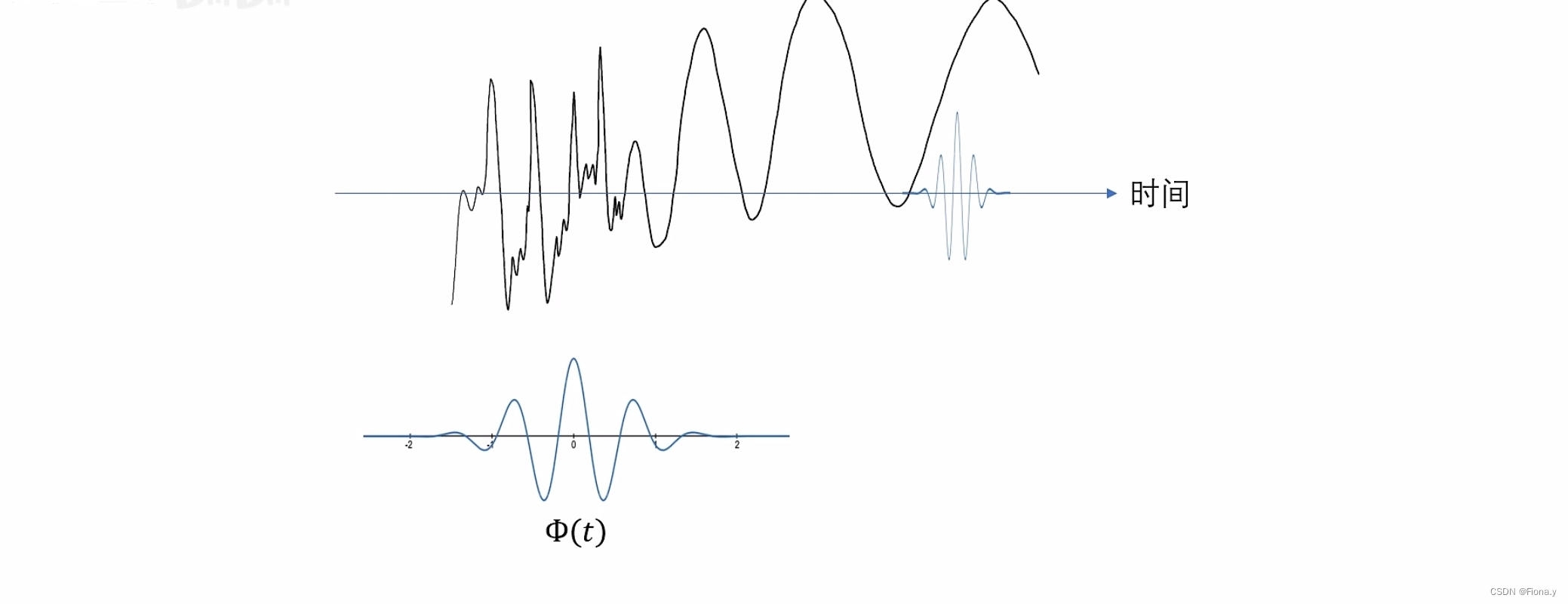
如何巡逻？

函数的平移：（t-b），b就是平移因子。不同的b值，对应着不同的时间点。

观察者的高低频如何控制？

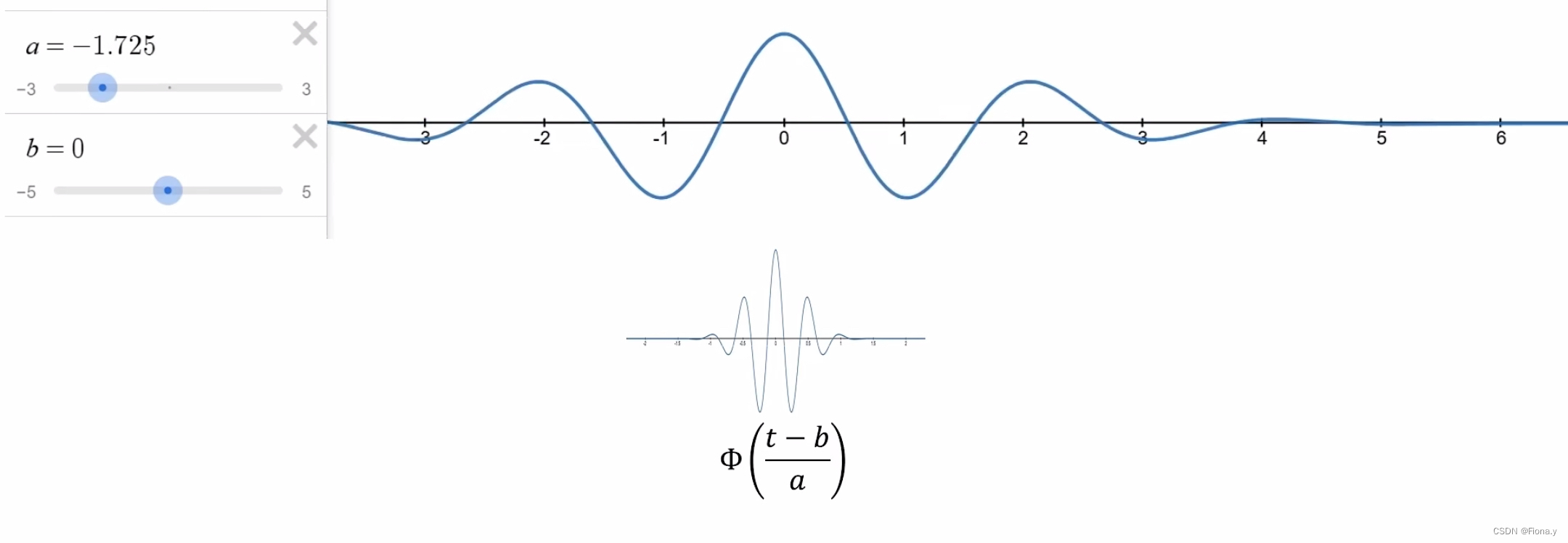
控制a，就能控制观察者的高低频。a也称为尺度因子。

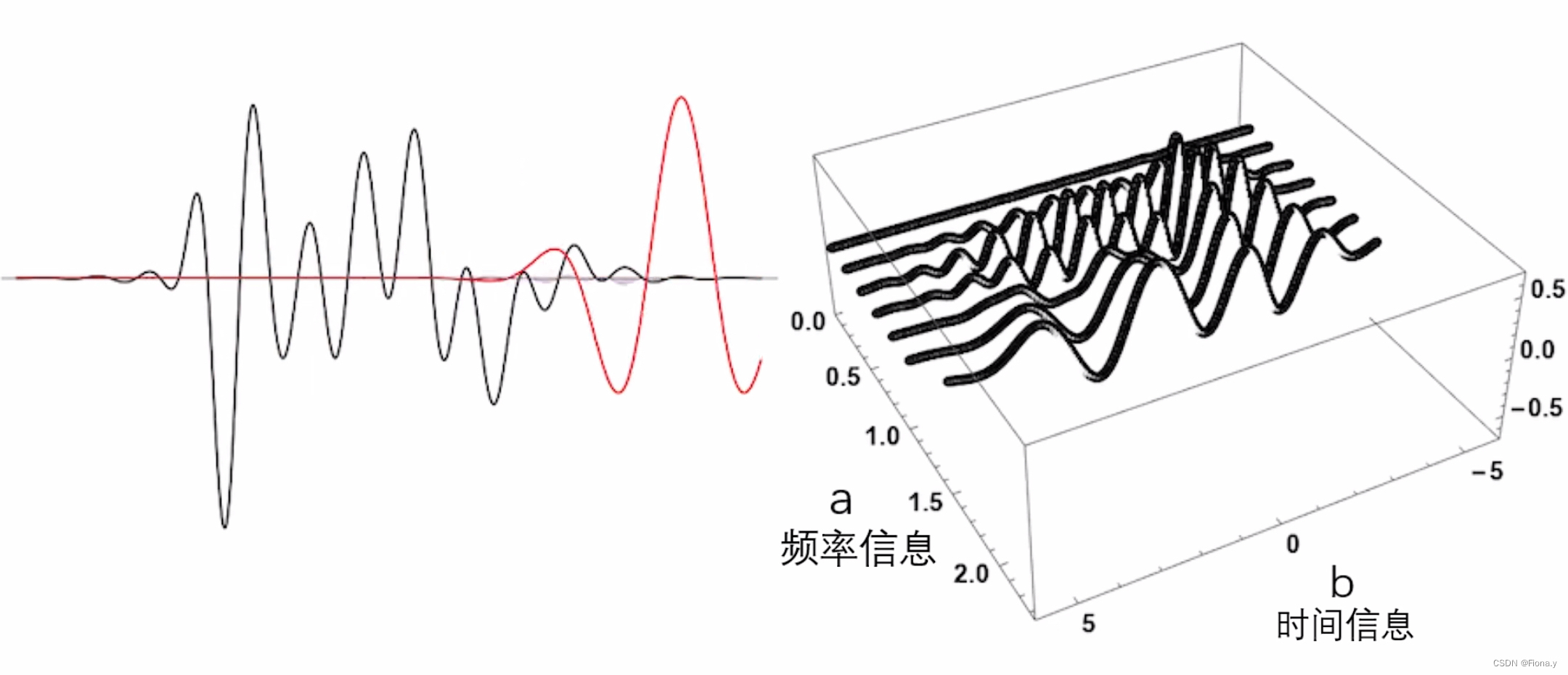
a越小，频率越高。

        左侧黑色：目标函数，红色观察者，右侧：直线为0，高频观察者与目标函数不像，为一条直线，调整a值，频率慢慢降下来，观察者巡逻查看目标函数是否与自己相像。b表示不同的时间，即巡逻观察。这是一个关于尺度因子a与时间因子b的二元函数图像。是一个三维图像。

七、小波变换结论

        小波变换能够同时得到时间和频率的信息，但并没有解决时频不确定的制约。这由数学的本质所确定。

小波，就是一系列在时间轴上做了局域化的观察者就是小波，(t)

不同需要下的小波是不同的，如下一部分：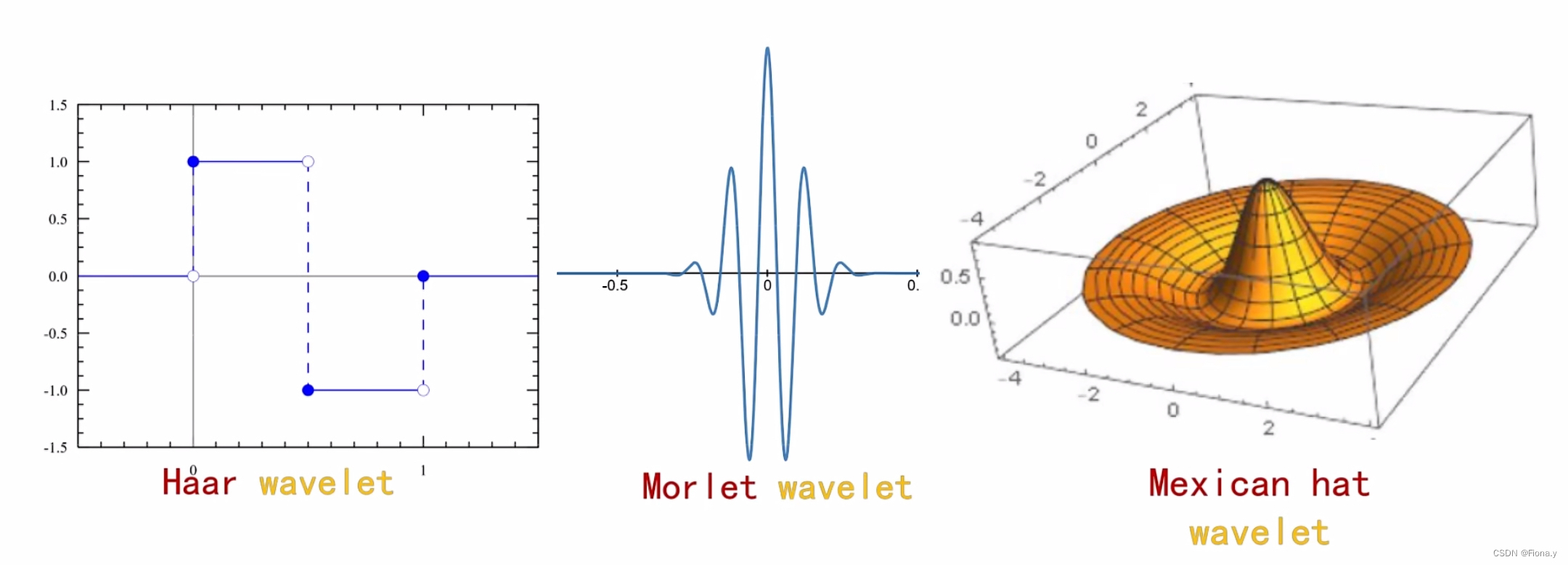

小波变换的公式：

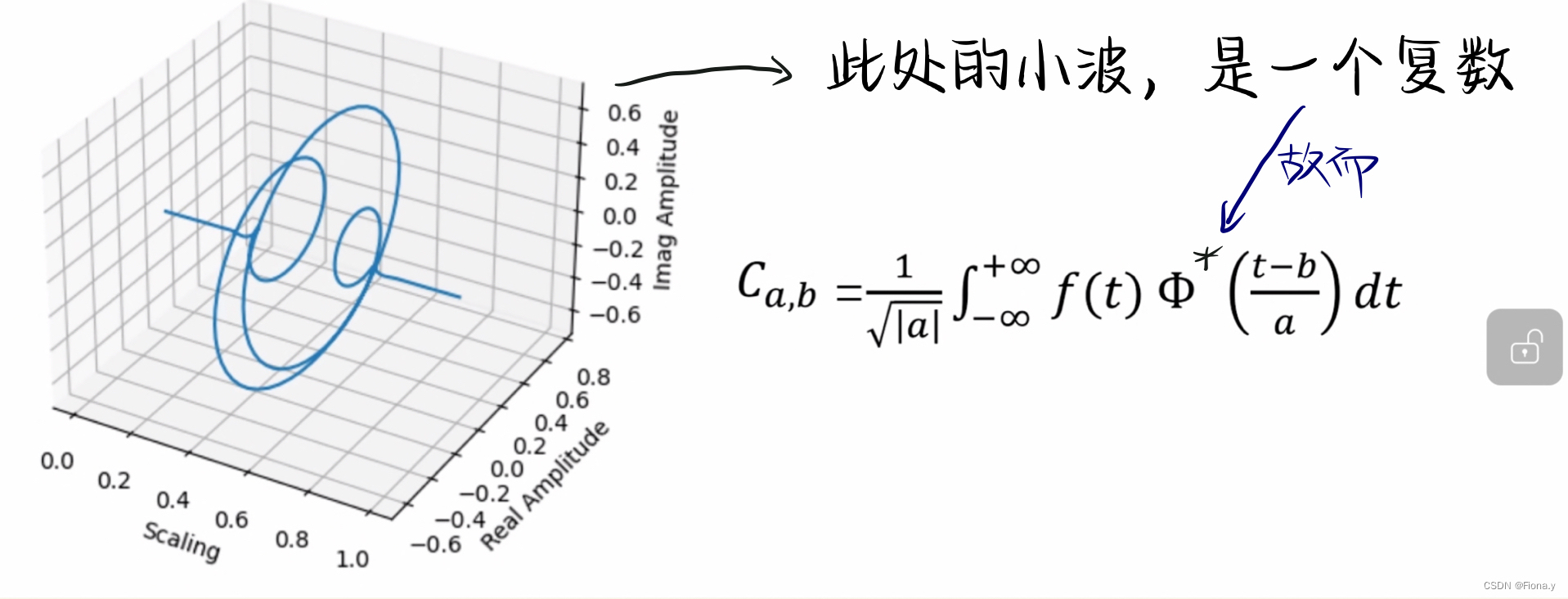
观察者在时间轴上滚动的和目标函数相乘求积分，即卷积。小波函数就是卷积和。

这篇关于何为小波变换？的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---