数据结构(3)--线性表实现一元多项式加法

本文主要是介绍数据结构(3)--线性表实现一元多项式加法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

参考书籍：数据结构（C语言版）严蔚敏吴伟民编著清华大学出版社

本文中的代码可从这里下载：https://github.com/qingyujean/data-structure

1.简要说明

一元多项式的表示和相加

多项式Pn(x)按升幂可写成：

Pn(x) = P0+P1*x+p2*x^2+...+Pn*x^n,

它由n+1个系数唯一确定，因此可用一个线性表p=(p0,p1,p2,...,pn),每一项的指数i隐含在系数pi的序号里。设Qm(x)是一元m次多项式，则可用线性表Q=(q0,q1,q2,...,qm)来表示。不失一般性，设m<n，则两个多项式想家的结果多项式Rn(x)=Pn(x)+Qm(x)可用线性表：

(p0+q0, p1+q1, ..., pm+qm, p(m+1), ..., pn)

    分析：
    对P、Q、R可用顺序存储结构，多项式相加的算法定义将十分简单，但通常应用中次数可能很高，使得顺序存储结构的最大长度很难确定；另外很多项的系数也可能为0，比如S(x)=1+3x^10000+2x^20000,如果是像这样仅有3个非0元素，则顺序存储结构的线性表的存储空间将非常浪费，故采用单链表结构，但是这时就要存储指数了。
    一元n次多项式Pn(x)=p1*x^e1 + p2*x^e2 +...+pm*x^em,其中pi是指数为ei的项的非零系数，且满足0<=e1<e2<...<em=n,若用一个长度为m且每个元素有两个数据项（系数项+指数项）的线性表（(p1,e1),(p2,e2),...,(pm,em)）便可唯一确定多项式Pn(x)。最坏情况下，n+1(=m)个系数都不为0，这种表示将大大节省空间。

    实现：
    "和多项式"链表中的节点无需另生成，而应该从两个多项式的链表中摘取。运算规则如下：假设指针qa、qb分别指向多项式A和B中当前进行比较的某个节点，则比较两个节点中的指数项，有下列3种情况：
     1.qa所指节点的指数值<qb所指节点的指数值，则应摘取qa所指节点插入到“和多项式”中；
    2.qa所指节点的指数值>qb所指节点的指数值，则应摘取qb所指节点插入到“和多项式”中；
     3.qa所指节点的指数值=qb所指节点的指数值，则将两节点的系数相加
          3.1若系数相加和数不为0，则修改qa所指节点的系数值，同时释放qb所指节点；
          3.2若系数相加和数为0，从多项式A的单链表中删除相应节点，并释放qa和qb所指节点。
    注意：
   表示一元多项式的应该是有序链表

2.代码实现

#include<stdio.h>
#include<stdlib.h>
#define NULL 0
typedef struct term{float coef;int expn;struct term *next;
}term, *LinkList;//term为一个新类型（是一个结构体），LinkList为指向这样的结构体的指针typedef LinkList polynomial;

int cmp(LinkList qa, LinkList qb){//比较项的指数大小if(qa->expn > qb->expn)return 1;else if(qa->expn == qb->expn)return 0;elsereturn -1;
}

//若有序链表L中存在与项t的指数相等的元素，则指针q指向L中第一个指数为t->expn的节点的位置，
//否则q指向第一个指数满足与t->expn相比>0的节点的前驱位置
bool locateElem(LinkList L, LinkList t, LinkList &q){LinkList p1 = L->next;LinkList p2 = L;//p2总指向p1的前驱while(p1){if(t->expn > p1->expn){p1 = p1->next;p2 = p2->next;}else if(t->expn == p1->expn){q = p1; return true;}else{//p1->expn > t->expn,因为L是有序表，所以如果程序走到了这一步，说明没找到与项t的指数相等的节点元素//则返回q的前驱结点q = p2;return false;}}if(!p1){//t->expn比当前列表所有元素的指数都大，则上面的while循环会因为p2到达了尾节点，p1=NULL而跳出q = p2;return false;}
}

//输入m项的系数和指数，建立表示一元多项式的带有头节点的有序链表P
//利用尾插法
void createPolyn(polynomial &P, int m){//先建立一个带有头节点的空链表，即初始化P = (polynomial)malloc(sizeof(term));P->next = NULL;LinkList r = P;//r指针总是指向当前线性表的最后一个元素，即尾元素printf("输入系数,指数,如项2x^5则输入(2,5):\n");//不必按升幂输入for(int i = 0; i < m; i++){//依次输入m个非零项LinkList t = (LinkList)malloc(sizeof(term));t->next = NULL;LinkList q;scanf("%f,%d",&t->coef,&t->expn);if(!locateElem(P, t, q)){//当前链表中不存在该指数项，则插入，此时q为链表中第一个指数>t->expn的节点的前驱结点t->next = q->next;q->next = t;}else{//当前列表中已经存在有节点元素的指数与本次输入的项的指数相同，所以本次输入无效，应重新输入i--;}}
}

//打印多项式链表
void printPolynomial(polynomial P){LinkList q = P->next;printf("打印多项式的线性表：[");while(q){printf("(%.2f,%d)  ",q->coef, q->expn);q = q->next;}printf("]\n\n");
}

//多项式加法：Pa=Pa+Pb,利用2个多项式的节点构成“和多项式”
void addPolyn(polynomial &Pa, polynomial &Pb){LinkList qa = Pa->next;LinkList qb = Pb->next;LinkList qc = Pa;//pc总是指向"和多项式链表"的最后一个节点float sumOfCoef;while(qa&&qb){switch(cmp(qa, qb)){case 1:qc->next = qb;qc = qb;qb = qb->next;break;case 0://当前比较的两项的指数相同sumOfCoef = qa->coef + qb->coef;if(sumOfCoef != 0.0){//系数之和不为0,则修改qa所指节点的系数，同时释放gb所指节点LinkList s = qb;//s即将被free掉qa->coef = sumOfCoef;qc->next = qa;qc = qa;qa = qa->next;qb = qb->next;free(s);}else{//系数之和不为0，则从多项式链表A中删除qa所指节点，并free掉qa、qb所指节点LinkList s1 = qa;LinkList s2 = qb;qc->next = qa ->next;//qc的位置不变,qa、qb向后移动qa = qa->next;qb = qb->next;free(s1);free(s2);}break;case -1:qc->next = qa;qc = qa;qa = qa->next;break;}//end switch}//end whileqc->next = qa?qa:qb;//插入剩余段free(Pb);//释放Pb的头节点
}

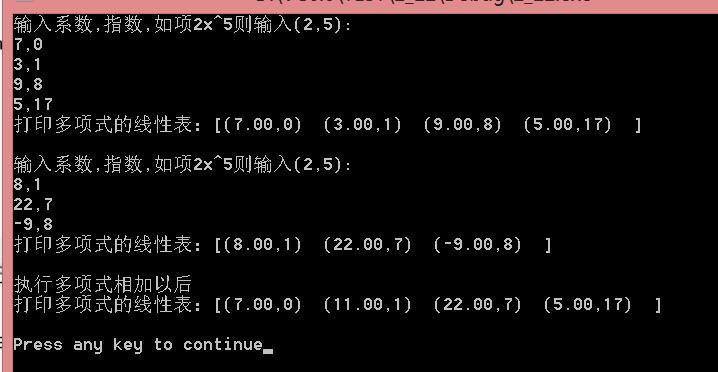
//实例：Pa(x)=7+3x+9x^8+5x^17, 输入((7,0),(3,1),(9,8),(5,17))
//Pb(x)=8x+22x^7-9x^8,输入((8,1),(22,7),(-9,8))
//和多项式为Pa(x) = 7+11x+22x^7+5x^17,即最后应该输出（(7,0),(11,1),(22,7),(5,17)）
int main(){polynomial Pa;createPolyn(Pa, 4);//初始化并创建多项式链表PaprintPolynomial(Pa);polynomial Pb;createPolyn(Pb, 3);//初始化并创建多项式链表PaprintPolynomial(Pb);printf("执行多项式相加以后\n");addPolyn(Pa, Pb);printPolynomial(Pa);return 0;
}