本文主要是介绍【计算机视觉】Lecture 13:相机投影2,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
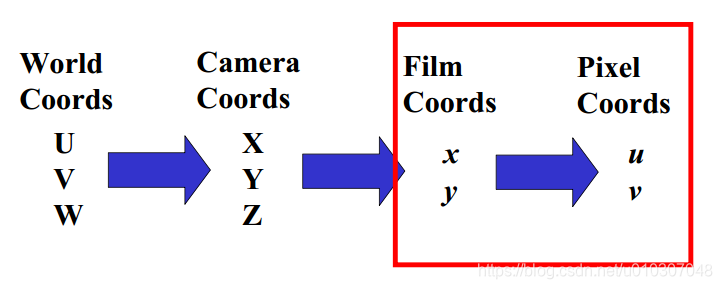
回忆:成像几何
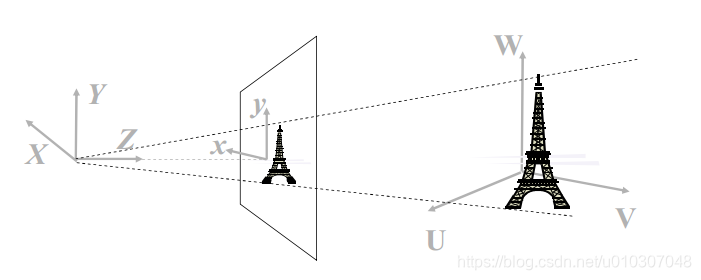
世界坐标系 (U,V,W) 中感兴趣的对象

成像几何
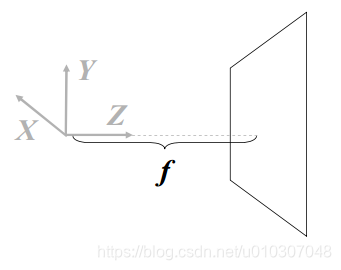
相机坐标系 (X, Y, Z)
Z是光轴
图像平面 (像素平面,成像平面) 位于沿光轴往外 f 个单位
f 称为焦距
成像几何
正向投影到图像平面 (像素平面,成像平面) 上。
三维(X,Y,Z)投影到二维(x,y)
成像几何
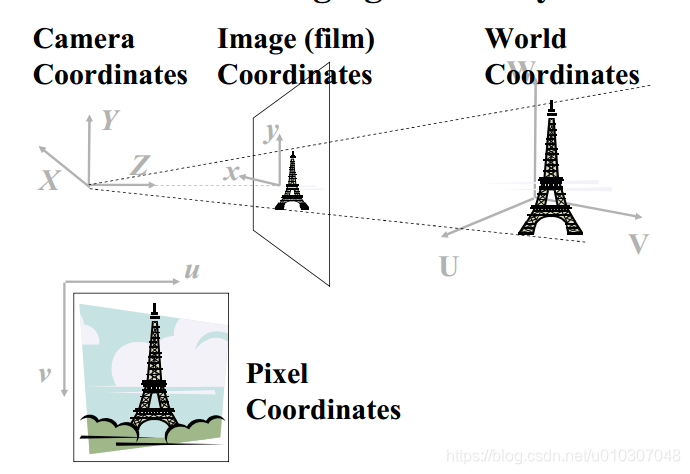
我们的图像被数字化成像素坐标(u,v)

成像几何
正向投影

我们需要一个数学模型来描述如何将三维世界点投影到二维像素坐标中。
我们的目标:用一个矩阵表达式来描述这个转换序列!
相机内参
仿射变换(Affine Transformation)
内参
描述成像坐标(投影图像)与像素阵列之间的坐标转换
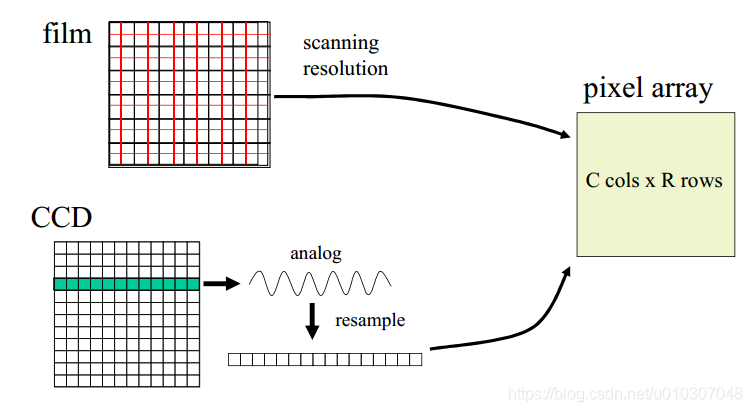
胶片相机:扫描/数字化
CCD摄像机:光传感器网格
内参(偏移)
成像平面(投影图像 film plane)
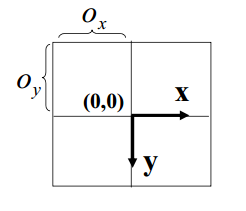
像素阵列
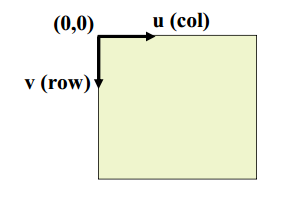
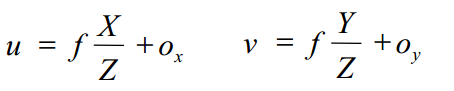
ox和oy称为图像中心或主点
注意:u是列,v是行
内参
有时会翻转一个或多个坐标轴

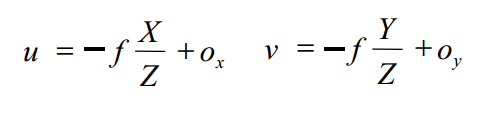
内参(尺度)
采样决定了图像中有多少行/列
有效尺度:sx和sy
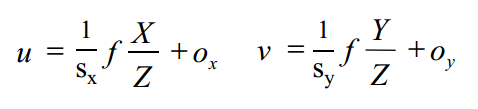
注意,因为我们在 x 和 y 中有不同的尺度因子,所以我们不一定有正方形像素块!
纵横比为 sy / sx
透视投影矩阵
将内参加入到透视投影矩阵:
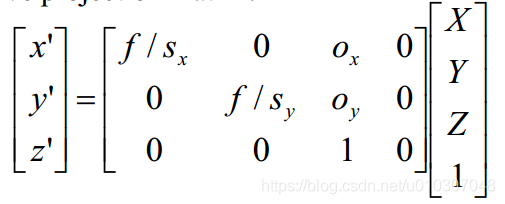
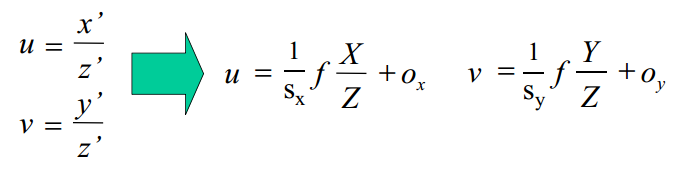
注意:
有时候,成像坐标系和相机坐标系是相反的方向:

注意2
一般来说,我喜欢把变换看作是从成像坐标(x,y)到像素坐标(u,v)的一个独立的二维仿射变换
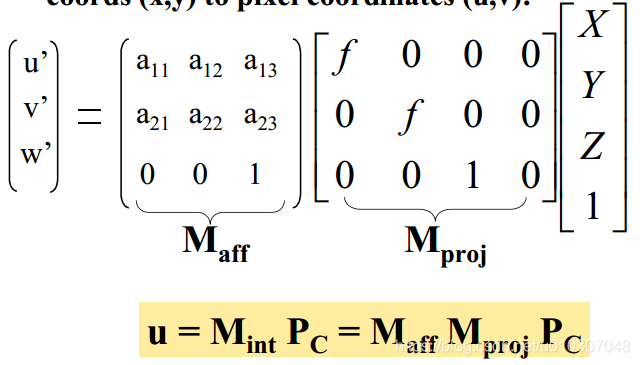
它是“仿射”变换,一种由6个参数定义的二维到二维的映射
Maff = [1/sx, 0, ox;
0, 1/sy, oy;
0, 0, 1]
总结:正向投影

总结:投影方程

这篇关于【计算机视觉】Lecture 13:相机投影2的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!