【补充】图神经网络前传—

本文主要是介绍【补充】图神经网络前传——PageRank，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

对于任何一个网页，都可以给出网页的重要度，给每个网页重要度打分，高分的靠前。

改变世界的谷歌PageRank算法_哔哩哔哩_bilibili

（这个参考资料考虑之后去自己看看）

把互联网用图来表示，每一个网页就是一个节点，网页之间的引用（放一个超链接，比如）就是边。不过现在可能这样就不太方便了，因为现在的网页是可以随时生成的（比如支付成功页面），同时还有无法触达的部分（比如朋友圈、聊天记录），都不是爬虫可以爬到的。

PageRank把互联网当作一个整体，认为网页间存在关联。之前的搜索引擎都是对孤立的网页进行分析（个人感觉这里就是，之前的方法只考虑了节点的特征，而忽视了结构关系，而PageRank除了节点信息之外也有边\结构的信息）

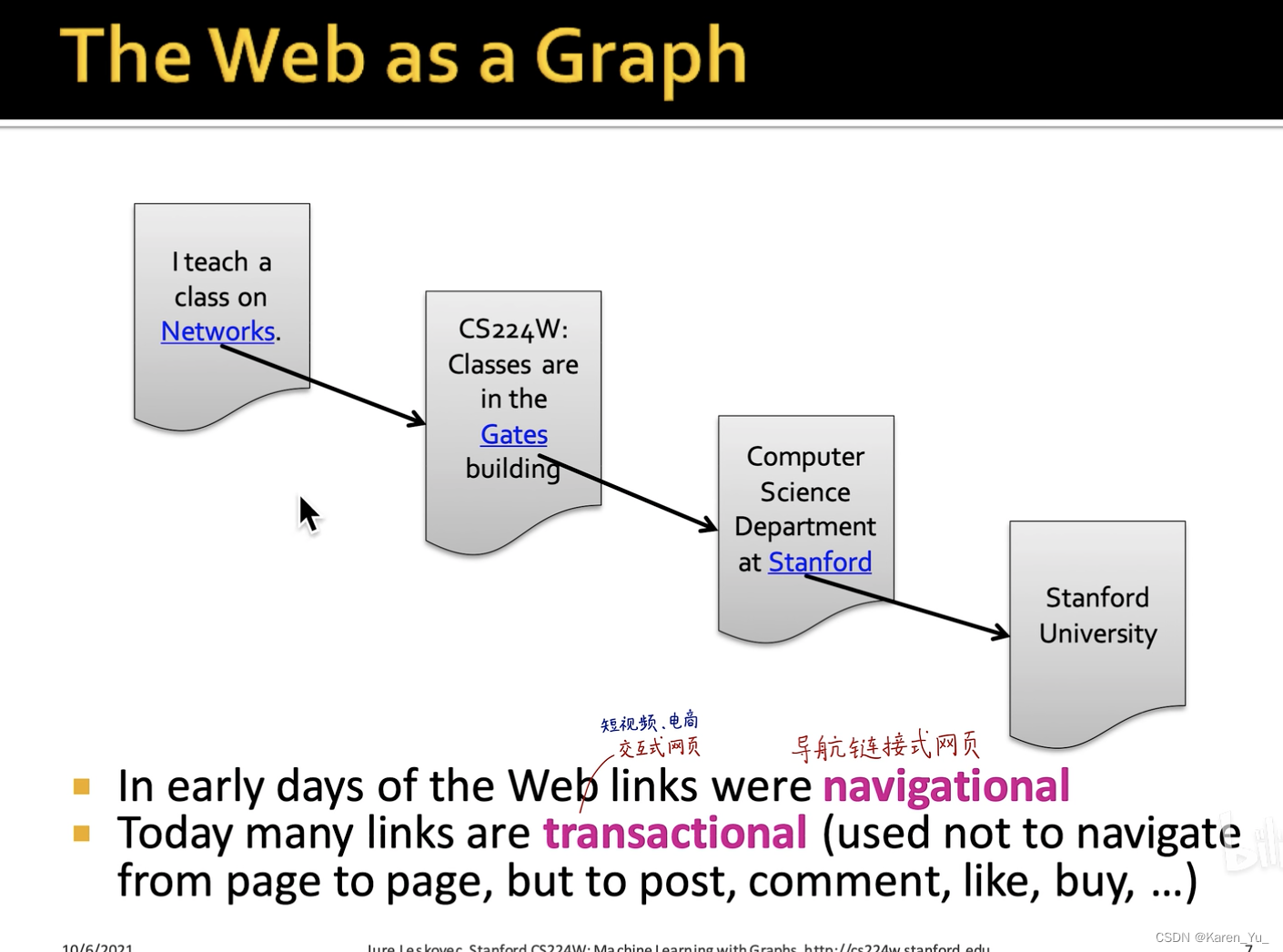
之前的网络可以表示成树状\层状结构（导航链接）->可以表示成有向图

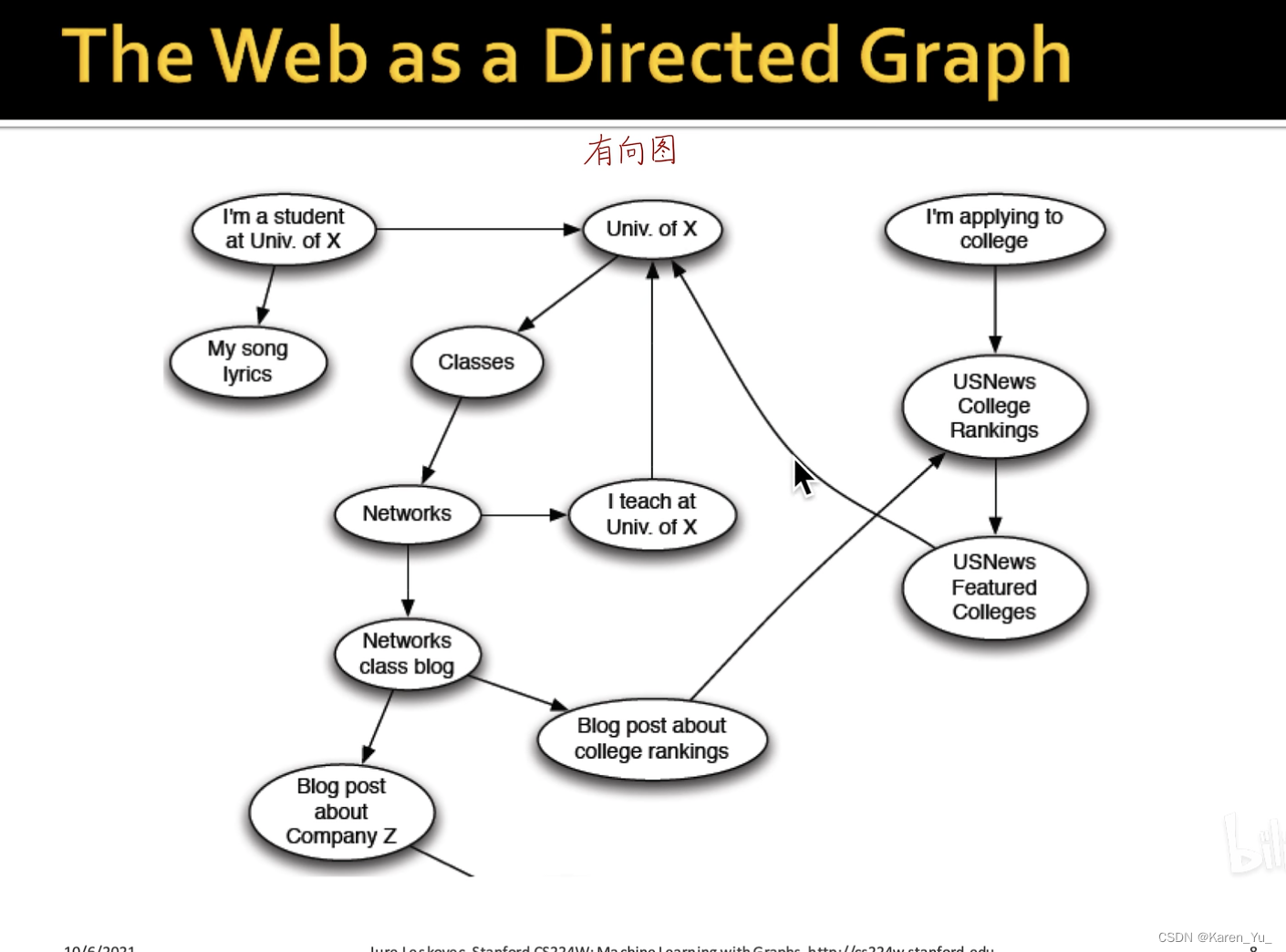
把整个互联网表示成一个有向图，有向图的节点是网页，网页之间的引用是连接。

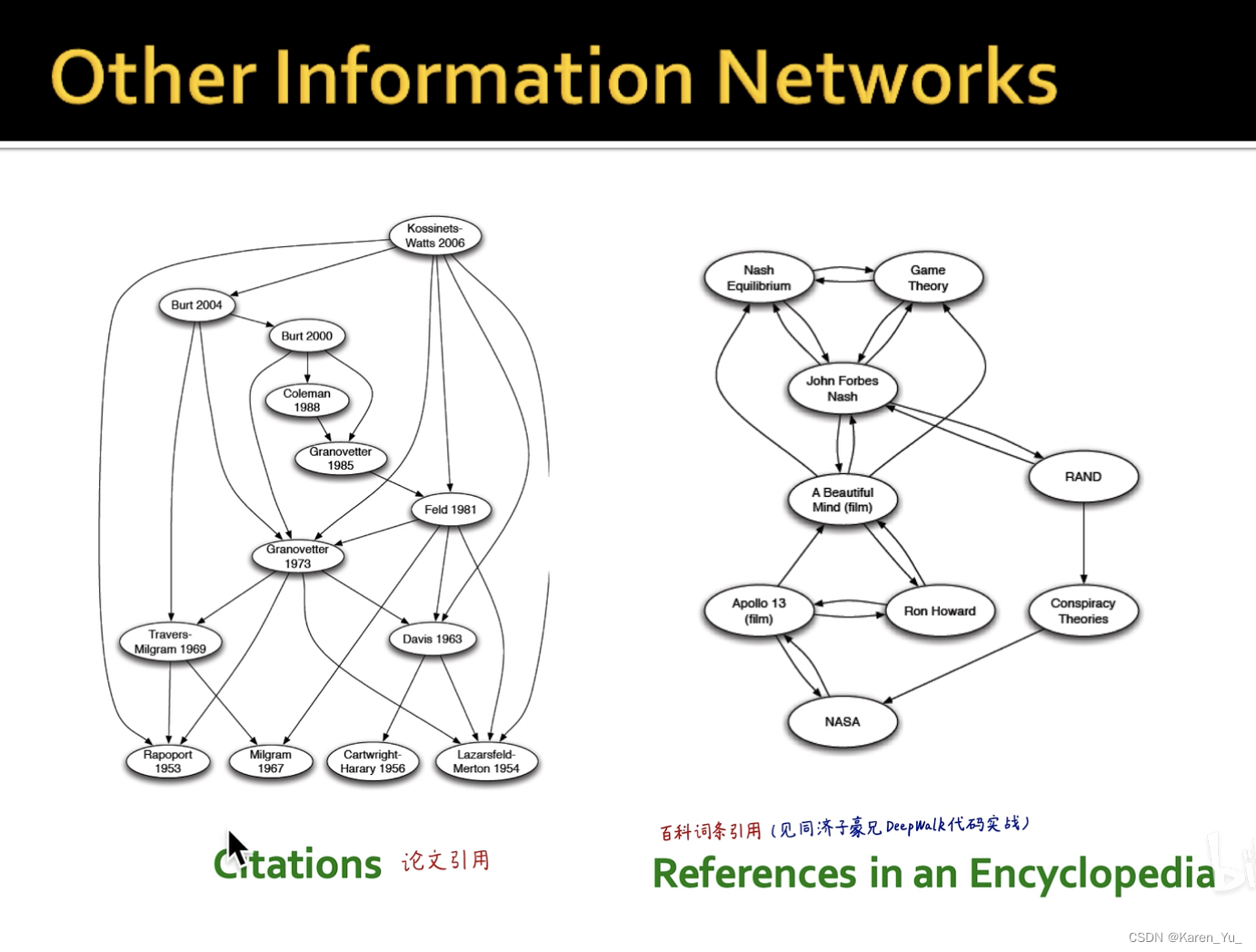
除此之外，论文之间的引用、百科词条之间的引用也可以被表示成图结构。甚至一个节点也可以引用自己。

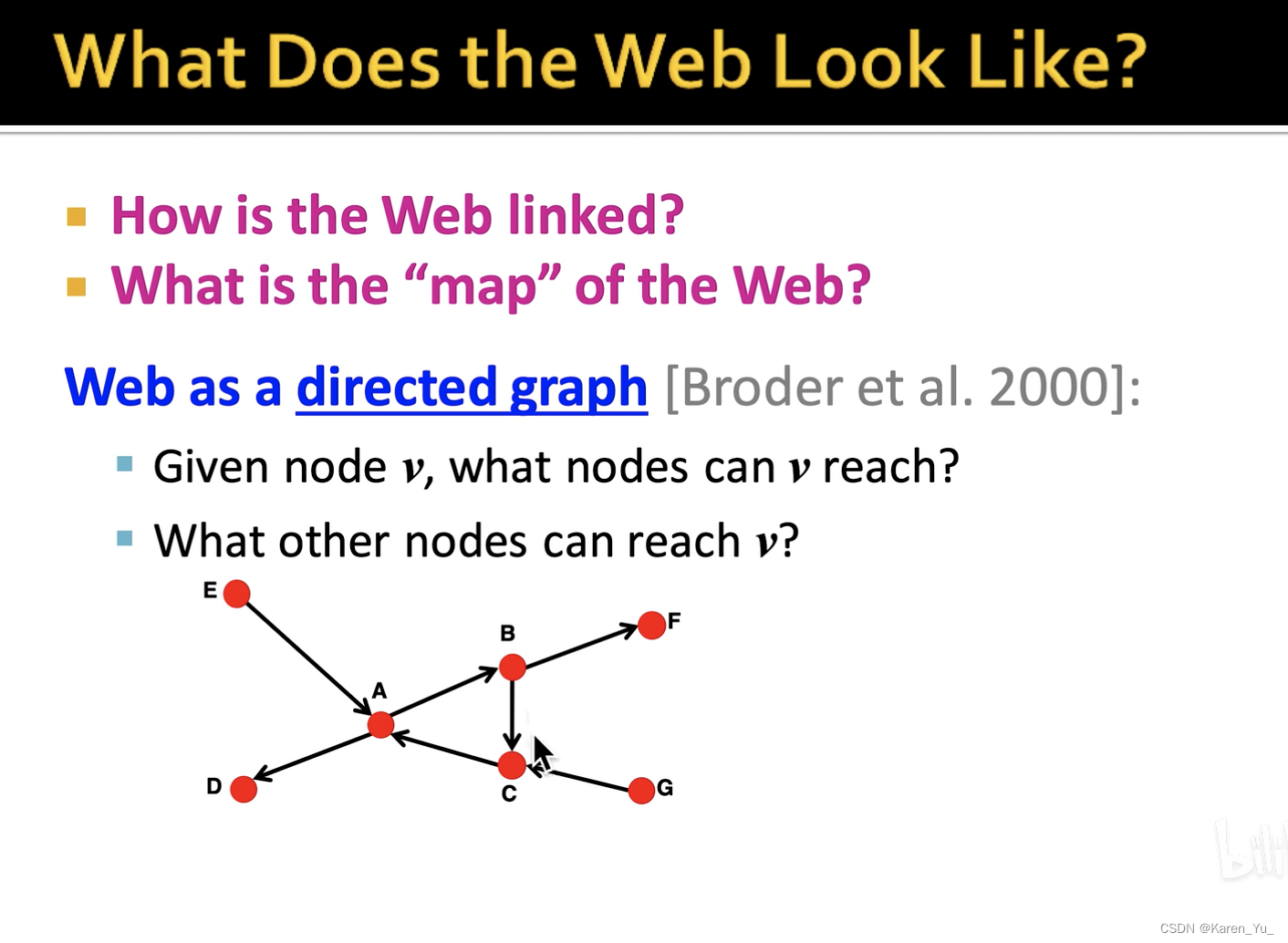
如果网页C中包含了网页A的链接，那么就有一条C指向A的边

现在，我们已经有了一张图，我们需要利用图的结构计算每个节点（网页）的重要度。并非所有网页都很重要。

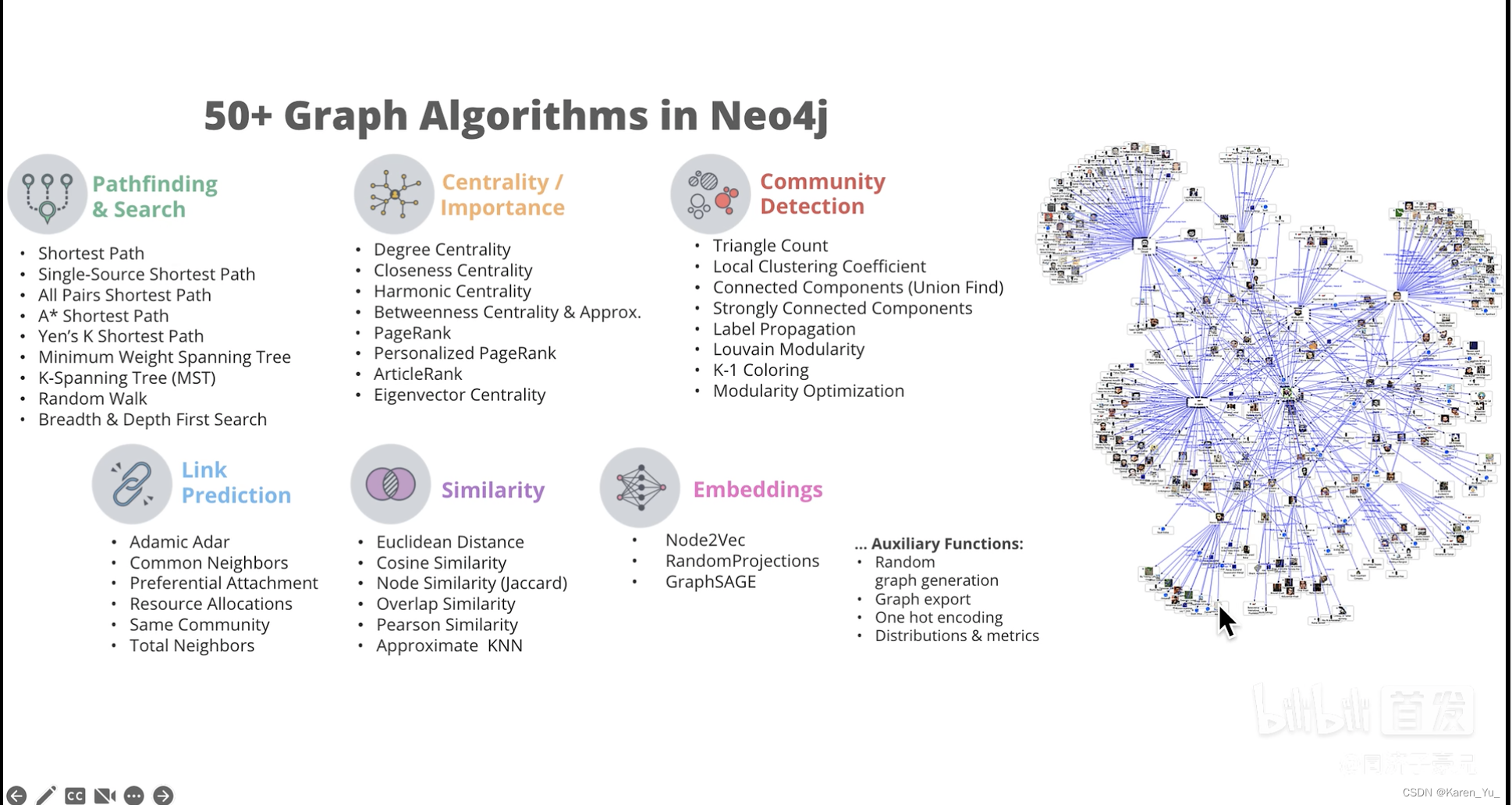
对于图而言，我们还可以做很多事情⬆️

PageRank做的是利用连接信息定量计算节点的重要度。PPR和Random Walk with Restarts是用来计算节点相似度的问题的（可以用在推荐系统里，定量地衡量两个用户的相似程度）。

PageRank

idea：把links当作是投票

这里link有两类：我引用别人的，别人引用我的。当然应采用别人引用我的（否则我自己引特别多链接直接屠榜显然不合理）-> in-coming links

显然不同的引用的重要程度也不同，不然我也可以自己创一些莫名其妙的网页指向自己（又屠榜了嘿嘿）。

PageRank采用的就是来自重要网页的vote更值钱。那么怎么知道是不是重要网页捏？要计算A网页的PageRank，就要计算所有引用网页A的网页的PageRank，要计算所有引用网页A的网页的PageRank，就要计算所有引用所有引用网页A的网页的网页PageRank……套娃了属于是。

->一个递归问题

先看第一个角度，线性方程组

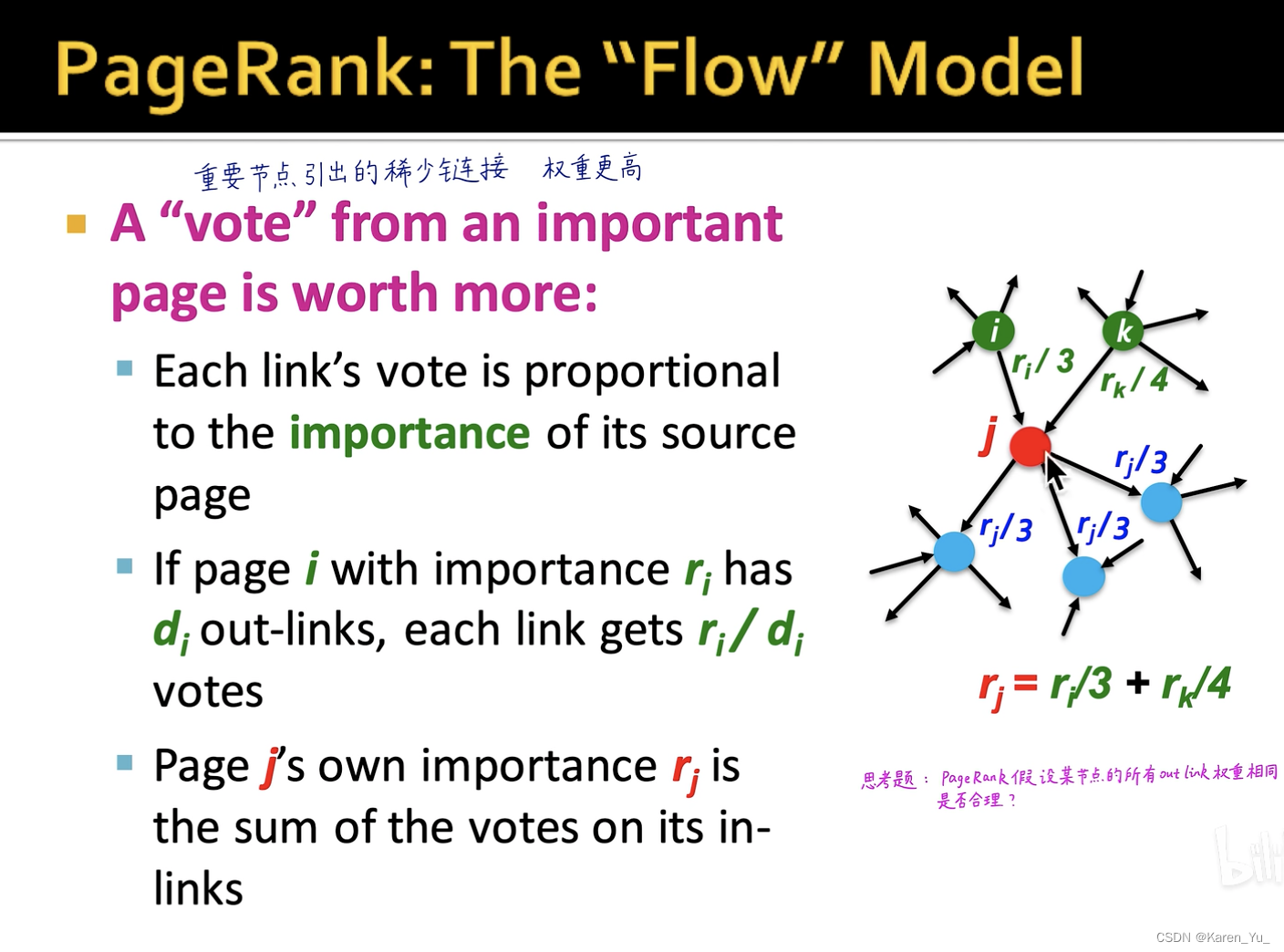
假设我们要计算红色节点j的PageRank，那么我们就首先找找谁引用了j节点，i节点的、k节点引用了j节点（绿色），蓝色的节点是j节点引用的，这里就不用看了。

对于i节点，有三条out-link（引用了三个节点），因此分给j节点的只有 $\frac{r_i}{3}$ ，这里 $r_i$ 表示的是i节点的PageRank，同理 $r_k$ 表示的是k节点的PageRank。k节点有四个out-link，所以给j节点的就是 $\frac{r_k}{4}$ 。因此，j节点此时 $r_j = \frac{r_i}{3} + \frac{r_k}{4}$ <-这时一次迭代。

这里假设了节点的所有out-link的权重是一样的（当然不是这样啦！）

理论上三个方程，三个未知数，完全可以求解了，但是实际上是一个方程两个未知数，因此需要补一个，需要补充一个方程，三个节点的PageRank求和=1:

$r_a + r_y +r_m = 1$

->联立方程组求解（高斯消元法）

现在，我们把网络扩大呢，这样解方程显然不经济实惠了。

看下面这个例子，A节点只有来自C节点的引用，而C节点有三个out-link->除以3

B节点有两个节点指向，A和C，A只有两条out-link->除以2，C有三条->除以3

最后可以得到下面的结果。

从图中可以看出C节点就是那个最重要的节点，而A节点就是最不重要的节点（这也符合直觉）。

下一个，左乘M矩阵

还是刚刚的例子：

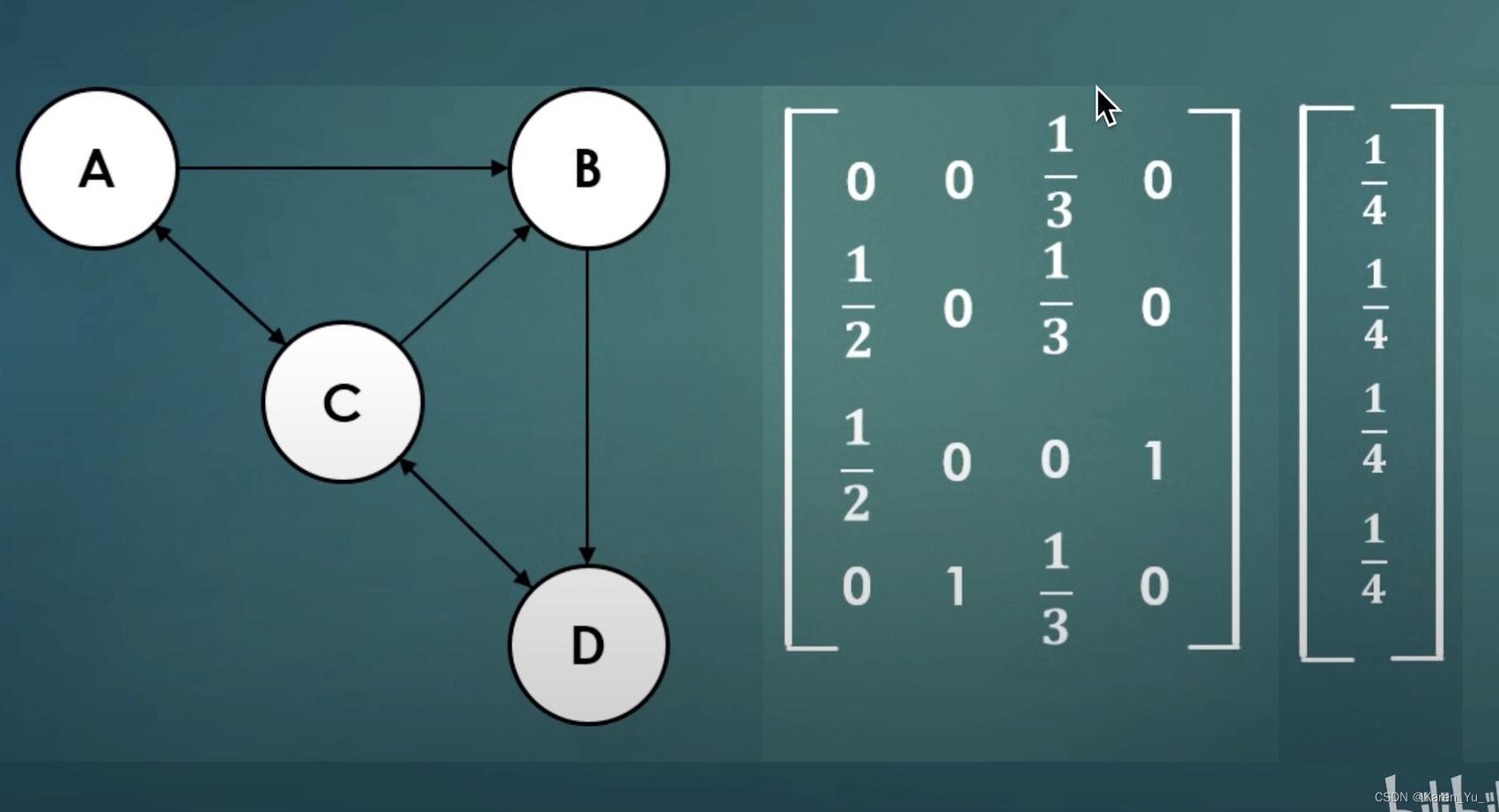
解释一下左边的矩阵，第3列就是C节点，C节点连着A B D，对每个节点都雨露均沾，都是1/3。

这个矩阵称为stochastic adjacent matrix $M$ ，右边的向量就是rank vector $r$

下一个是特征向量：

有一些线性变换只改变长度不改变方向->特征向量

看这里：10 - 特征向量与特征值_哔哩哔哩_bilibili

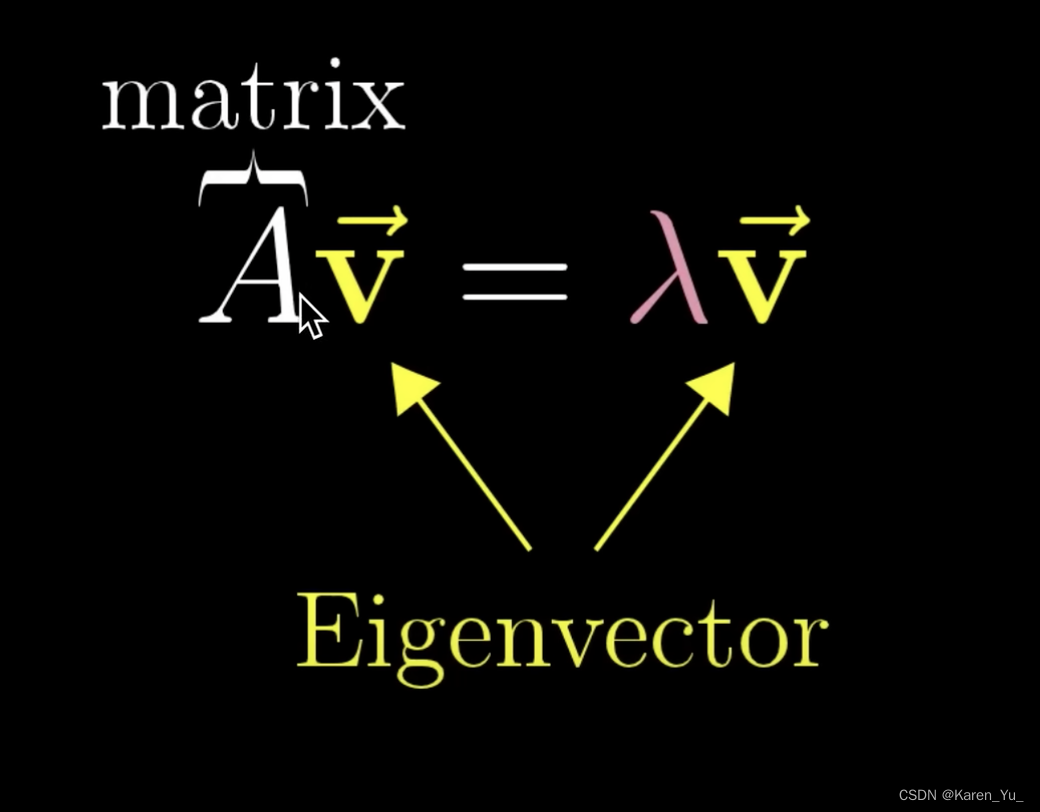
现在我们回到上面的M矩阵：

那么其实r就是这个特征向量，而1就是特征值

下一个角度是随机游走：

可以认为在这个有向图中，有一个浏览者在顺着连接随机游走，如果一个网页访问的次数比较多->这个网页比较重要->归一化为概率

马尔可夫链：

此时，求解PageRank就是求解stationary distributions of Markov Chains

求解

不停地左乘M矩阵，直到下一时刻的PageRank和当前时刻没有太大变化。

两种奇怪的网页（可能会为PageRank的计算带来困难）：

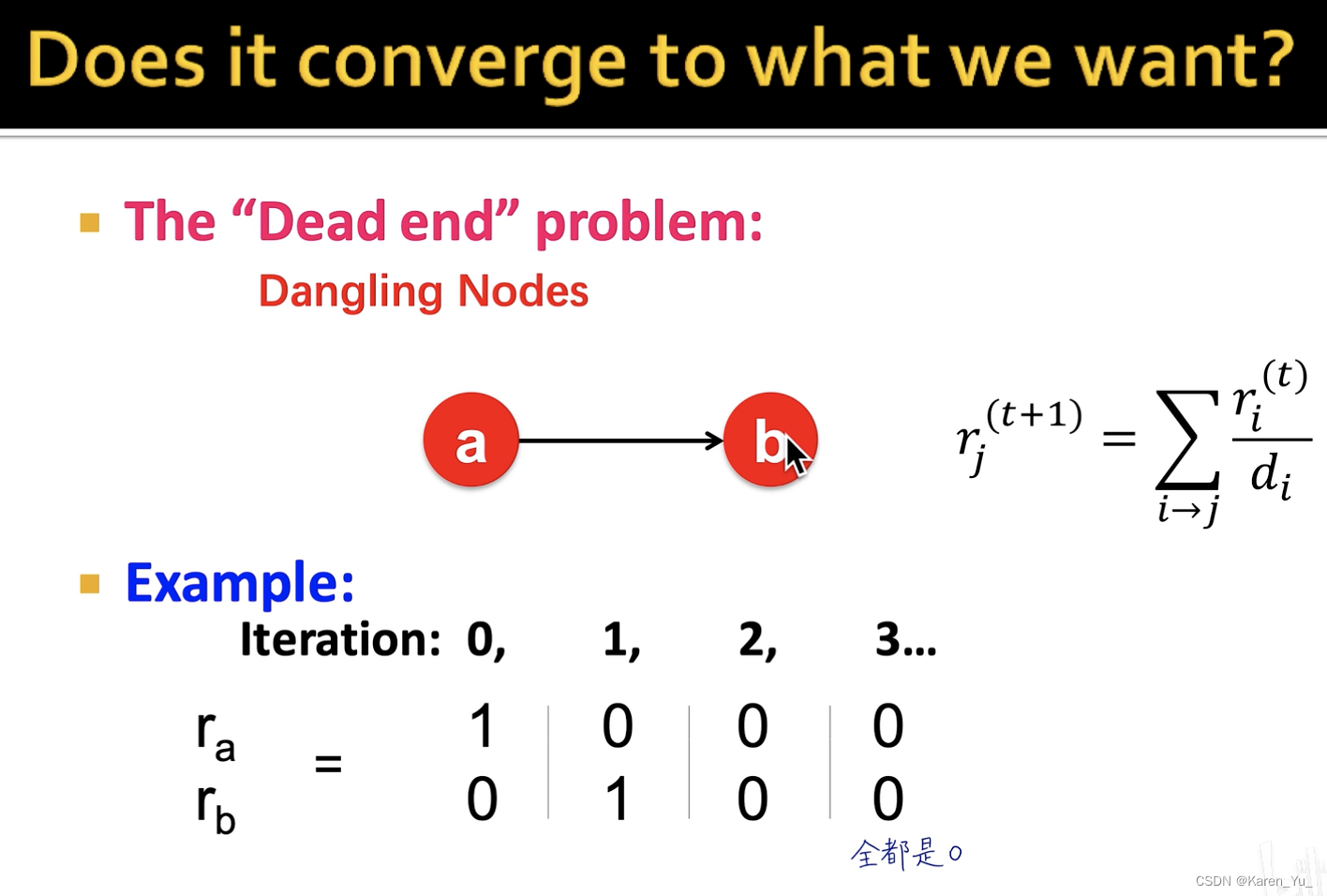
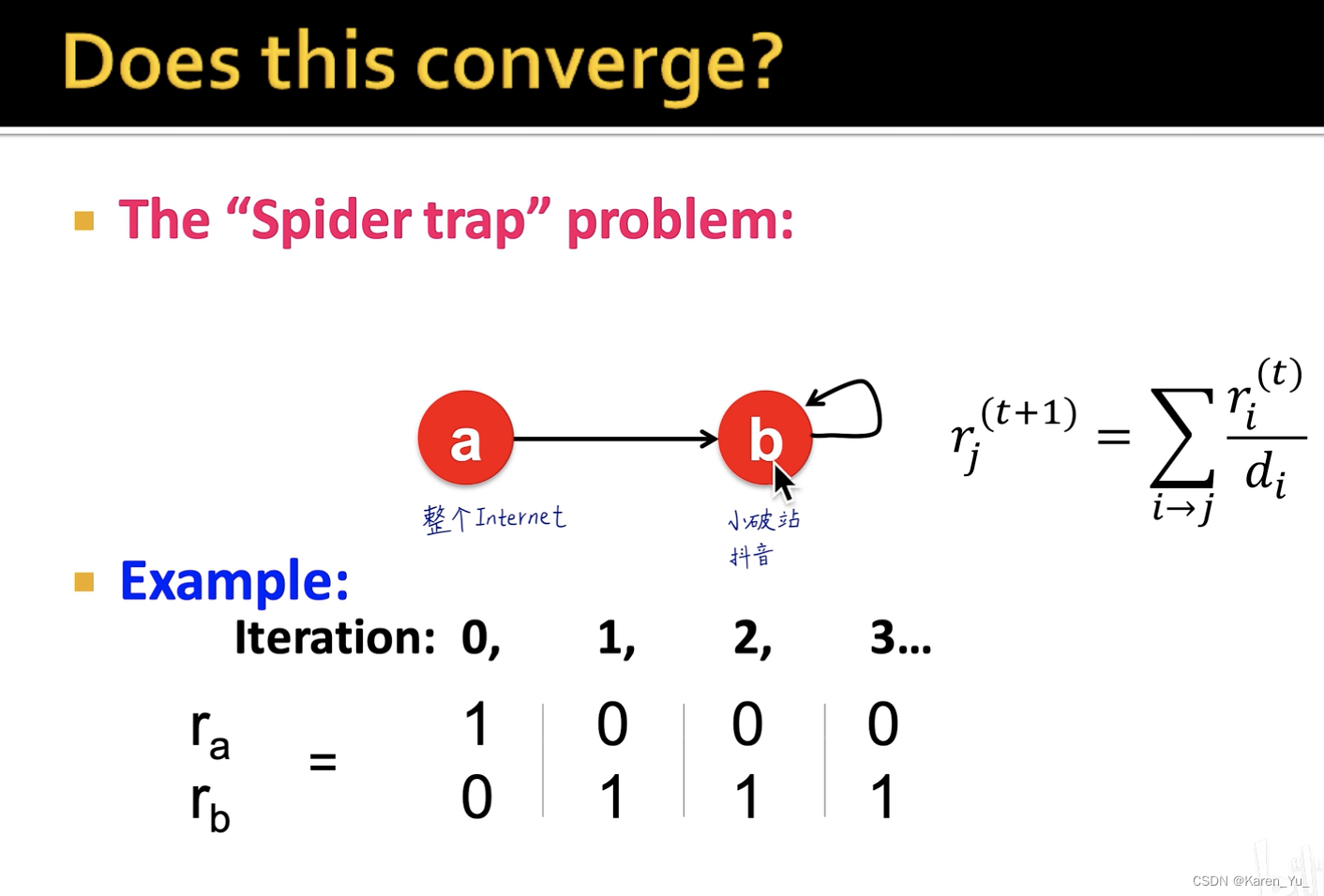
像这样其实违反了我们的假设，即M的每一列求和都应该为0

->如何解决

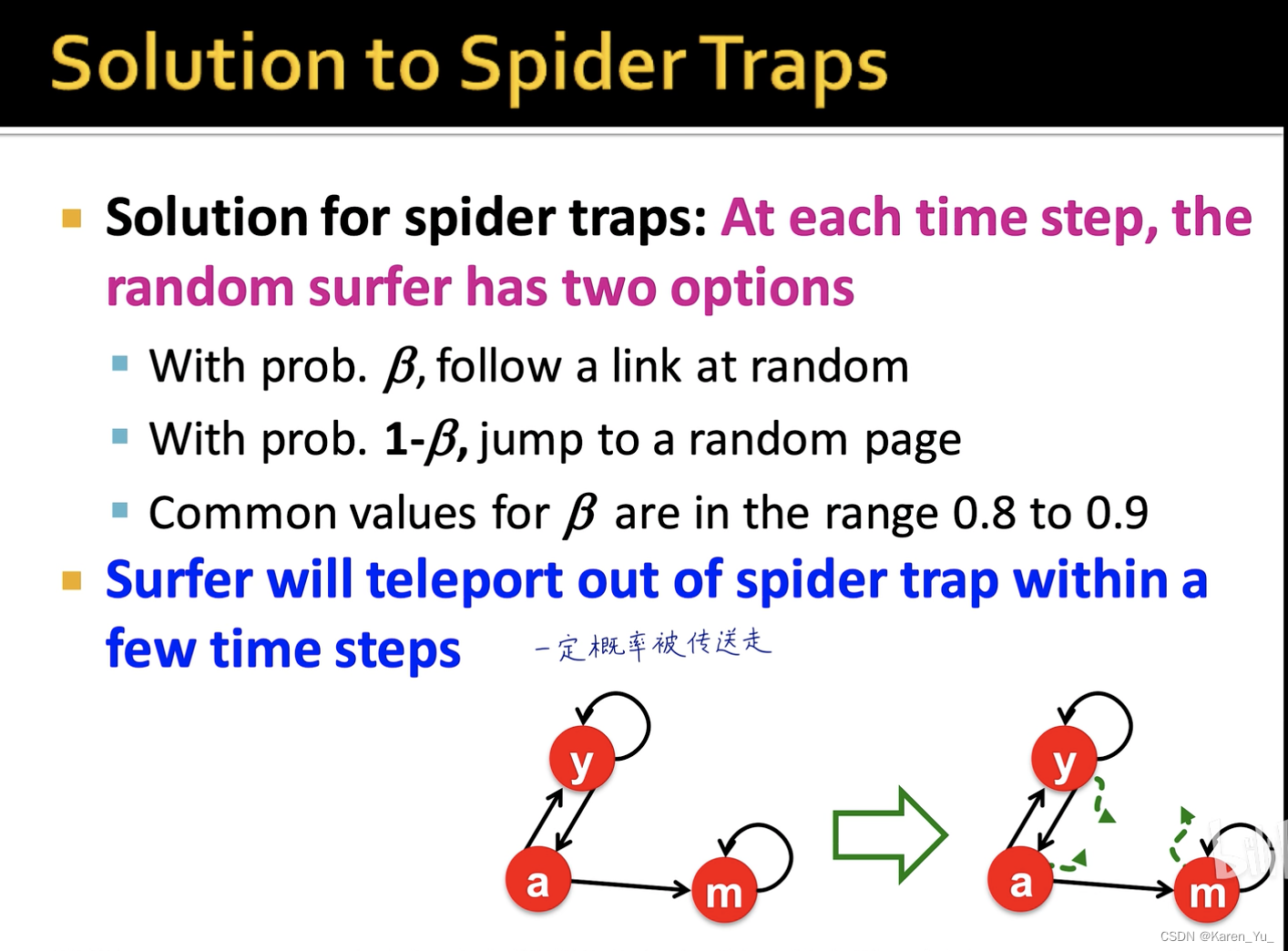
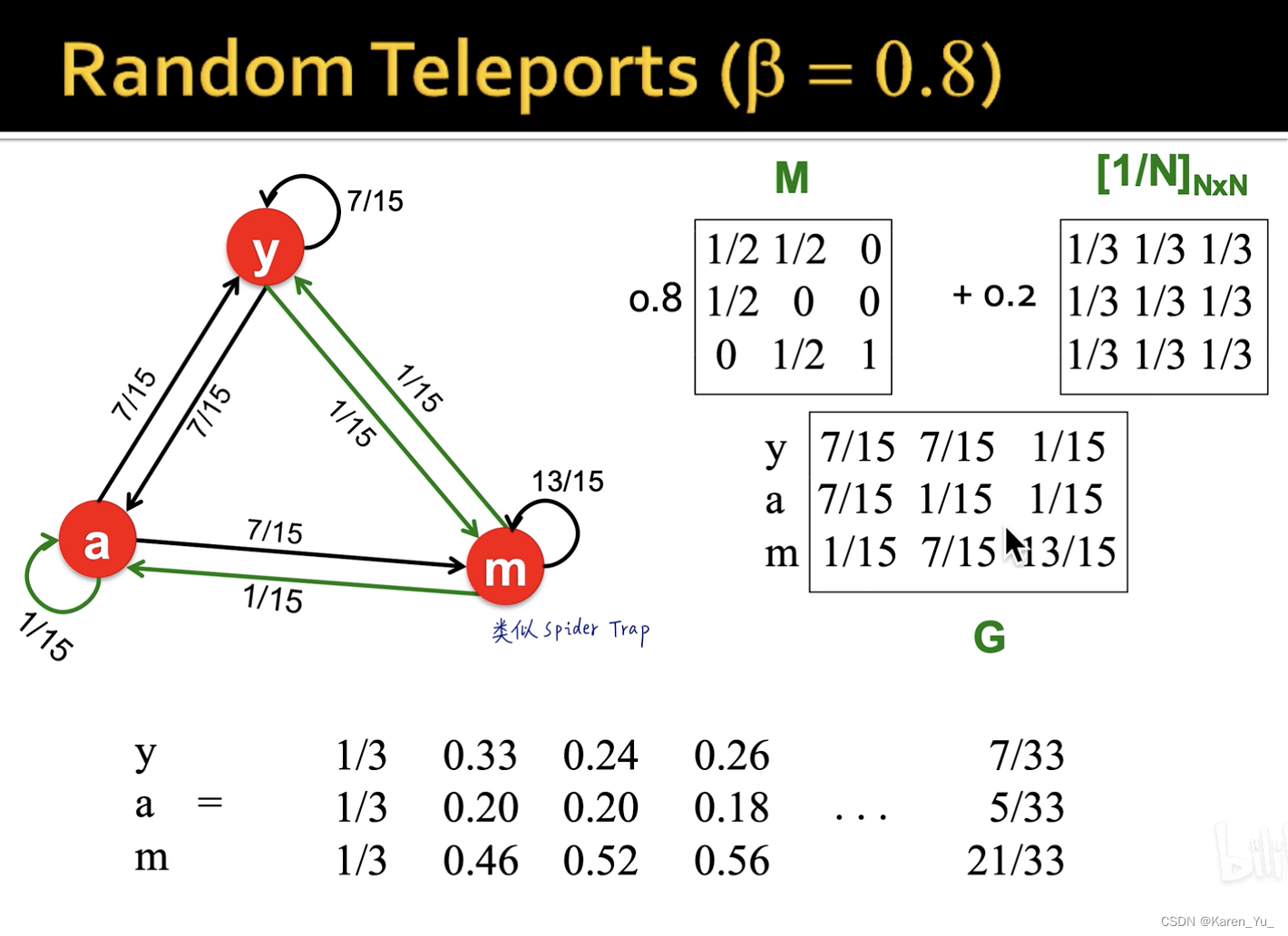
防止在一个网页里来回绕，有一定概率传送出去

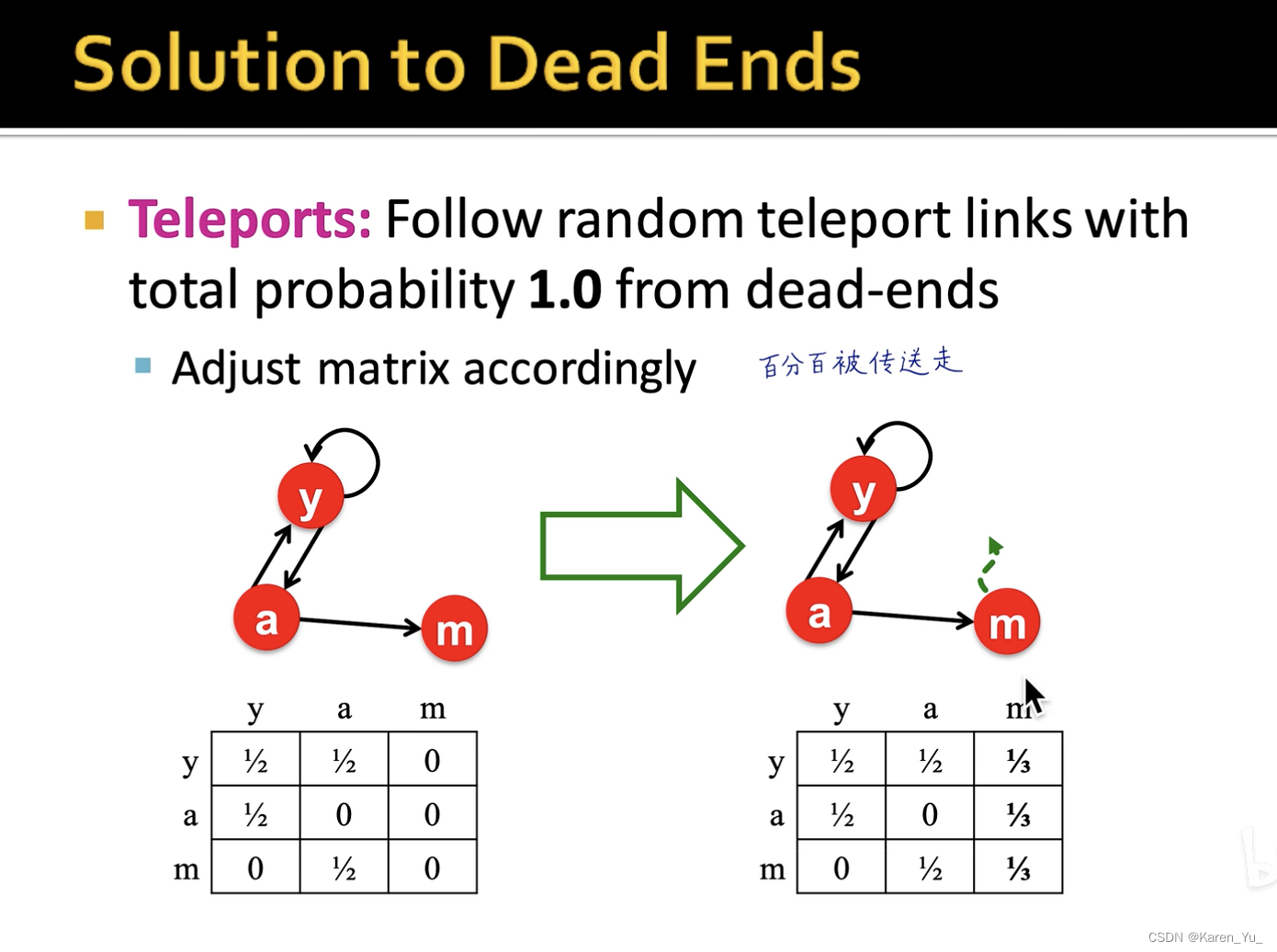
对于死胡同节点，百分百被传送走

Random walk with restarts and personalized PageRank

计算相似度

比如这里：相似的商品，相似的用户，这样比较好做推荐。

->寻找与指定节点最相似的节点

这里有一个基本假设是：被同一个用户访问过的节点，更有可能是相似的。

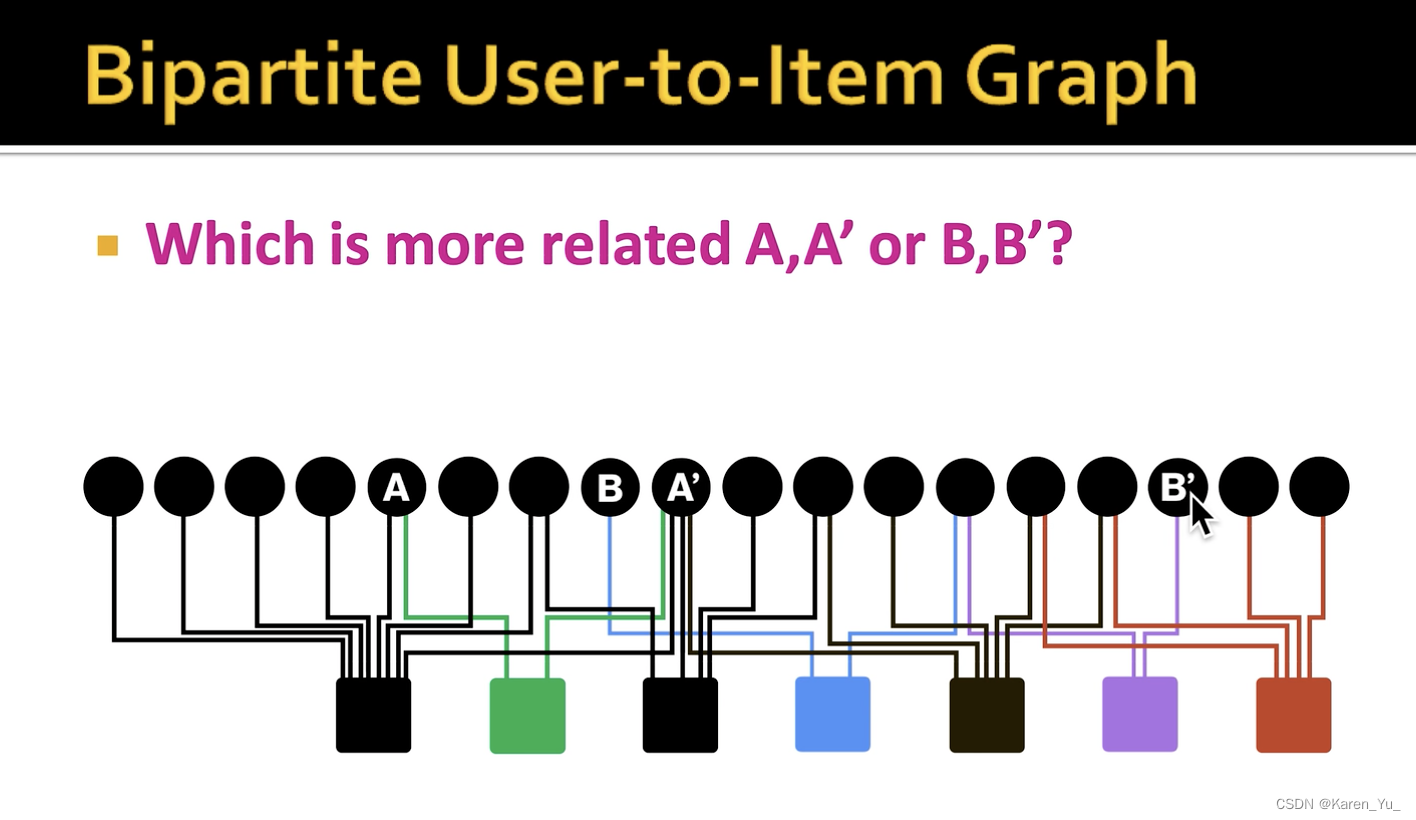
在这个例子里 $A$ 和 $A'$ 商品就可能更相似，都被绿色用户买过，相比之下，从 $B$ 到 $B'$ 就要从蓝色用户到紫色用户

这些交互方式，怎么定量衡量？

回顾PageRank方法

->随机传送->但是随机传送到目的不是任意节点了，而是指定的一个/一些节点

用随机游走的访问次数，来反映节点之间的亲疏远近

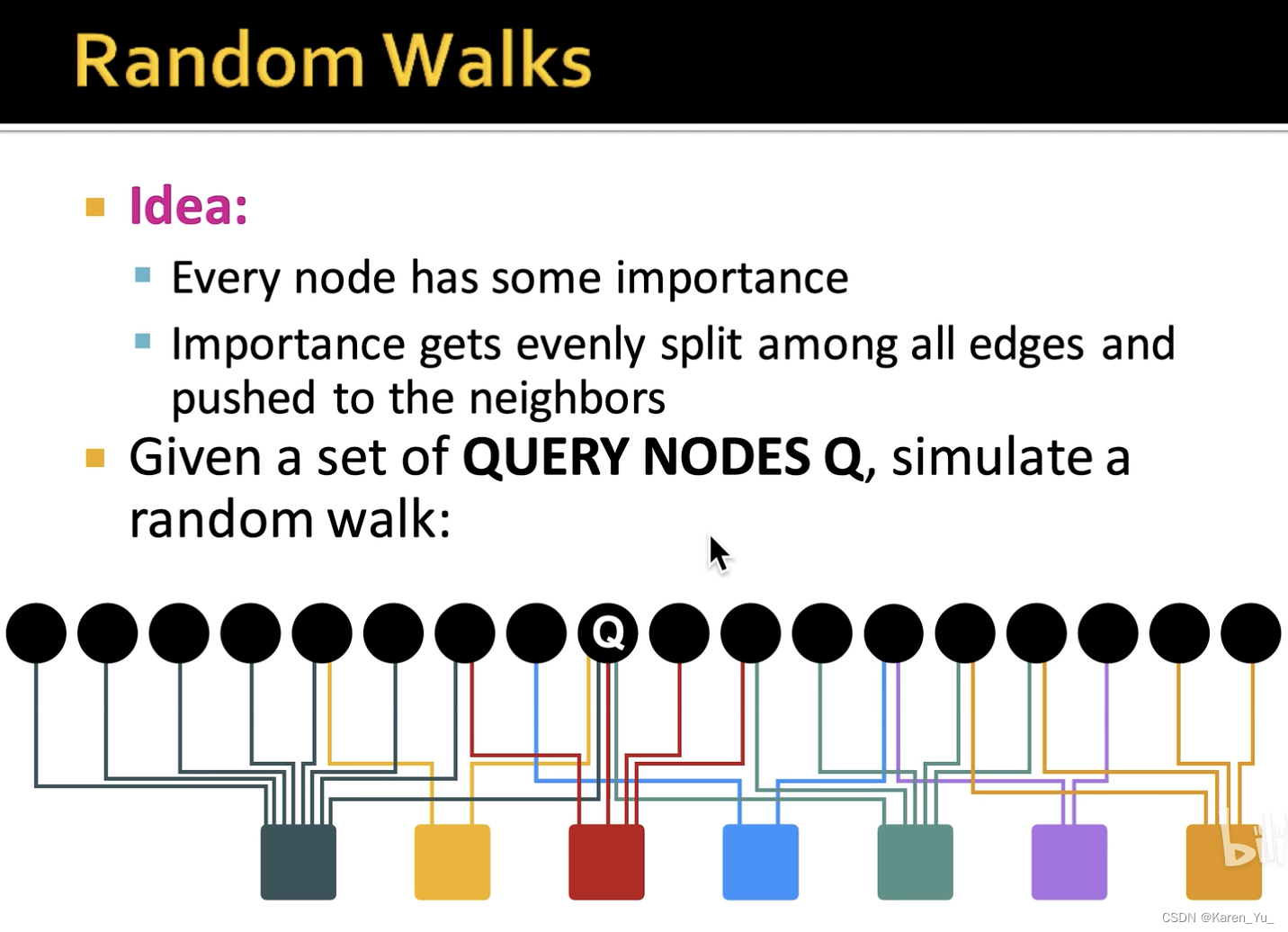
每次都以给定概率随机传送回Q节点

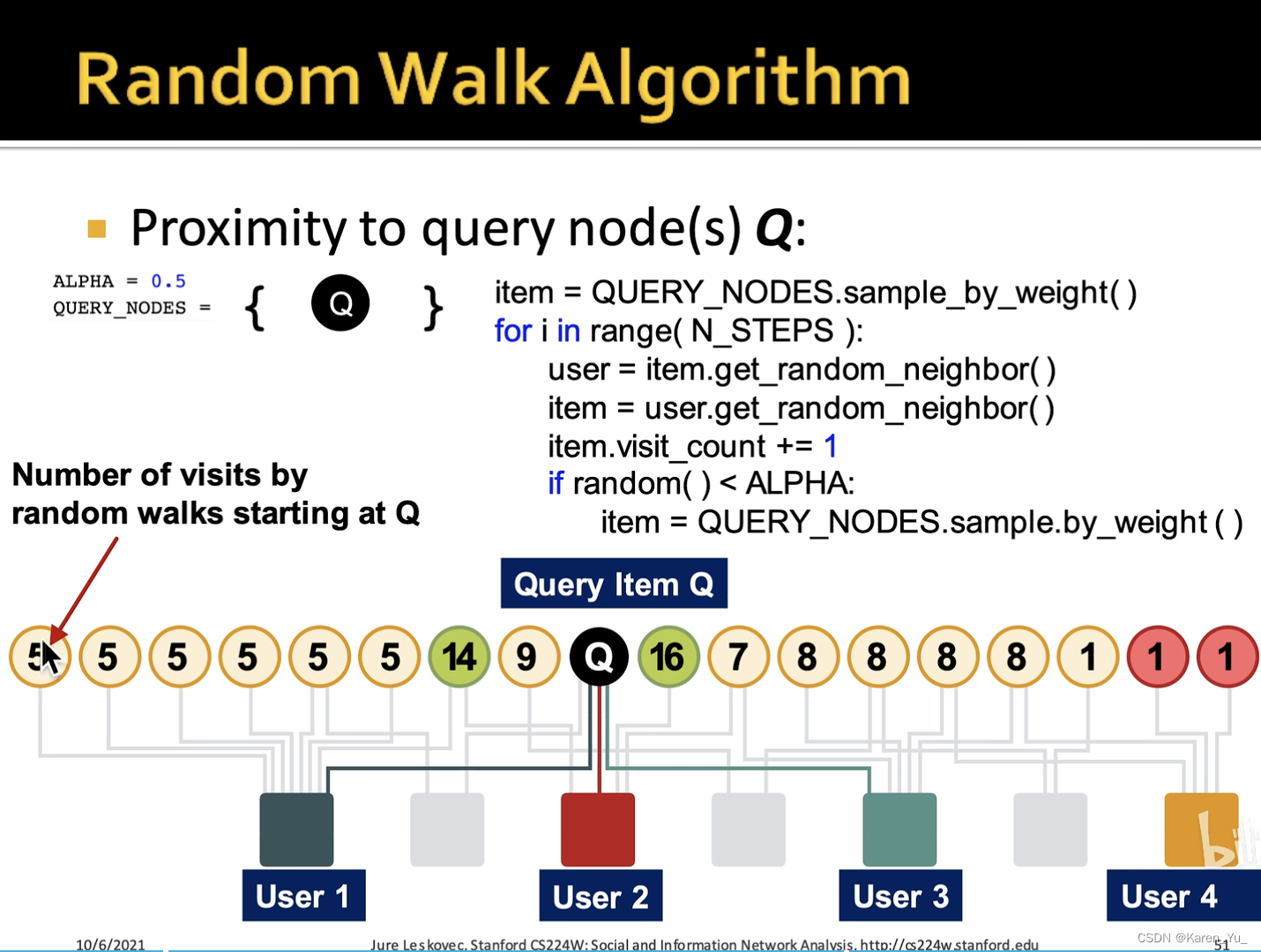
->可以用这些数字来反映这些商品与Q节点的相似度

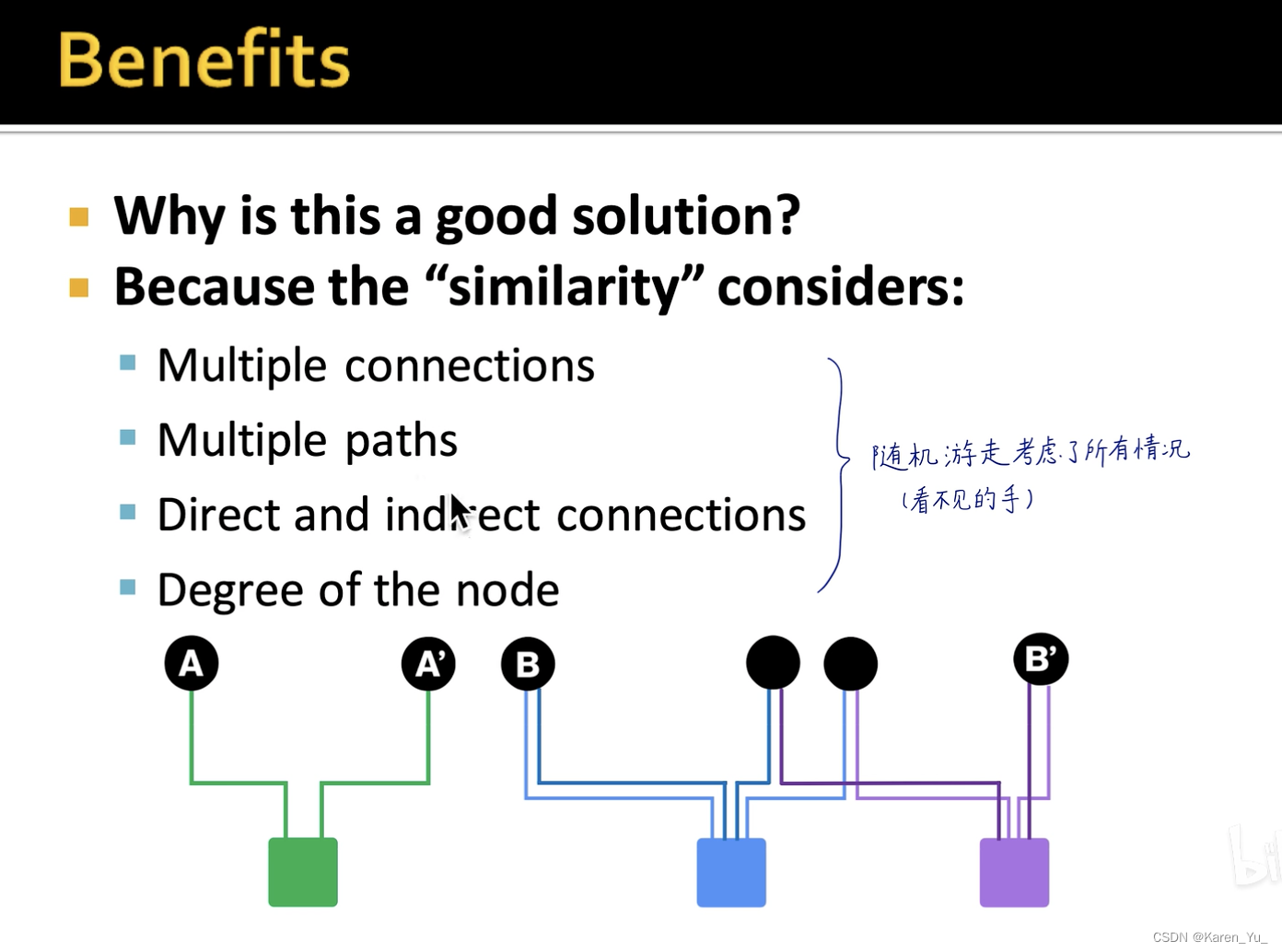
好处：考虑了所有的情况

使用PageRank

import networkx as nx
# 创建有向图
G = nx.DiGraph() 
# 有向图之间边的关系
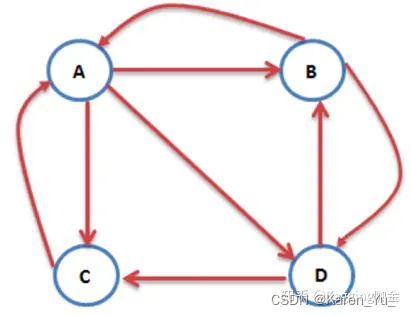
edges = [("A", "B"), ("A", "C"), ("A", "D"), ("B", "A"), ("B", "D"), ("C", "A"), ("D", "B"), ("D", "C")]
for edge in edges:G.add_edge(edge[0], edge[1])
pagerank_list = nx.pagerank(G, alpha=1)
print("pagerank值是：", pagerank_list)

pagerank值是： {'A': 0.333, 'B': 0.222, 'C': 0.222, 'D': 0.222}

⬆️来源：机器学习十大经典算法-PageRank（附实践代码） - 知乎

这里的alpha就是阻尼系数。

什么是阻尼系数？

$P_n = dM\cdot P_{n-1} +(1-d)P_0$

这里， $P_n$ 表示第n步计算得到的PageRank值， $d$ 表示阻尼系数， $M$ 表示转移矩阵， $P_0$ 是初始PageRank值（即：1/页面（节点）个数）

下面是迭代的方式：

import numpy as np
def  nodes2matrix(node_json):
"""
构建图的
"""node2id = {}dim = len(node_json)for id_ , key in enumerate(node_json.keys()):node2id[key] = id_   matrix = np.zeros((dim,dim))for key in node_json.keys():nodeid = node2id[key]for neighbor in node_json[key]:neighborid = node2id[neighbor]matrix[neighborid][nodeid] = 1for i in range(dim):matrix[:,i] = matrix[:,i]/sum(matrix[:,i])return matrixdef pagerank(matrix, iter_ = 10, d=0.85):length = len(matrix[0])inital_value = np.ones(length)/lengthpagerank_value = inital_valuefor i in range(10):pagerank_value = matrix@pagerank_value* d  +  (1-d)/lengthprint("iter {}: the pr value is {}".format(i, pagerank_value))return pagerank_value

⬆️来源：鼎鼎大名的PageRank算法——理论+实战 - 知乎

其他参考：

如何优雅的理解PageRank - 简书

PageRank算法详解 - 知乎

这篇关于【补充】图神经网络前传——PageRank的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！