本文主要是介绍ccsu 1042 斐波那契II 矩阵快速幂,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目是求f(n)mod10000以后的斐波那契数,n的范围是0<= N <= 10^9。这样的数据范围就只能考虑矩阵相乘+二分了。
矩阵相乘求斐波那契:
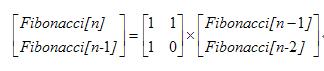
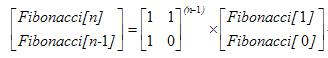
在二分的函数那里要注意的几点就是:当(n-1)为偶数进行二分以后,要返回单位矩阵,(n-1)为奇数就返回[1,1,1,0];
而为什么当此时的n为奇数的时候要进行一次矩阵相乘的运算呢?可以举个例子:二分(n-1)=7: 7->3->1 。当为1以后return到上一次的调用函数,此时进行矩阵相乘的函数运算,所得是2次方的矩阵而不是要求的的3次方的矩阵,所以还要单独求一次。
有一个人的博客上写了非常详尽的斐波那契的那种算法:
http://www.cnblogs.com/CCBB/archive/2009/04/25/1443441.html
有时间看看~。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstdlib>
#include<cctype>
using namespace std;
struct matrix{
long int a[2][2];
};
long int mod=10000;
matrix mul(matrix x,matrix y,long mod)
{
matrix b;
b.a[0][0]=(x.a[0][0]*y.a[0][0]+x.a[0][1]*y.a[1][0])%mod;
b.a[0][1]=(x.a[0][0]*y.a[0][1]+x.a[0][1]*y.a[1][1])%mod;
b.a[1][0]=(x.a[1][0]*y.a[0][0]+x.a[1][1]*y.a[1][0])%mod;
b.a[1][1]=(x.a[1][0]*y.a[0][1]+x.a[1][1]*y.a[1][1])%mod;
return b;
}
matrix pow(matrix x,int n,long mod)
{
matrix ret,tmp;
if(n == 0)
{
ret.a[0][0]=1;ret.a[0][1]=0;
ret.a[1][0]=0;ret.a[1][1]=1;
return ret;
}
if(n == 1)
return x;
tmp=pow(x,n/2,mod);
ret=mul(tmp,tmp,mod);
if(n%2!=0)
ret=mul(ret,x,mod);
return ret;
}
int main()
{
long int n;
matrix ans;
while(cin>>n)
{
if(n == -1)
break;
ans.a[0][0]=1; ans.a[0][1]=1;
ans.a[1][0]=1; ans.a[1][1]=0;
if(n)
{
ans=pow(ans,n-1,mod);
cout<<ans.a[0][0]<<endl;
}
else
cout<<"0"<<endl;
}
}
这篇关于ccsu 1042 斐波那契II 矩阵快速幂的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




