jdk1.8 HashMap红黑树插入修正源码分析

本文主要是介绍jdk1.8 HashMap红黑树插入修正源码分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

预备知识点

进入代码分析之前简要介绍相关知识点，推荐一个视频，讲得很好：

• youtube：https://www.youtube.com/watch?v=5IBxA-bZZH8
• bilibili：https://www.bilibili.com/video/av14050857

红黑树

红黑树是一种平衡二叉树，除了二叉搜索树的基本特征外还有以下特征：

• 所有节点分红黑两色
• 根节点和空叶子为黑色
• 不能出现相连红色节点
• 从根节点到任意叶子节点的路径上具有相同数量的黑色节点

红黑树的插入策略

分两步：

• 插入一个红色节点（红色需要修正的概率更小）
• 通过变色和旋转来修正修正违反上述规则之处

红黑树的插入新节点后的5种情况

其中一种没有违反任何规则，无须修正：

• 插入节点的父节点为黑色

插入新节点后的树可能不符合红黑树的定义，需要修正。红黑树的插入修正分4种情况：

1. 插入的节点为根节点
2. 插入节点的叔叔节点为红色
3. 插入节点的叔叔节点为黑色（三角式）
   
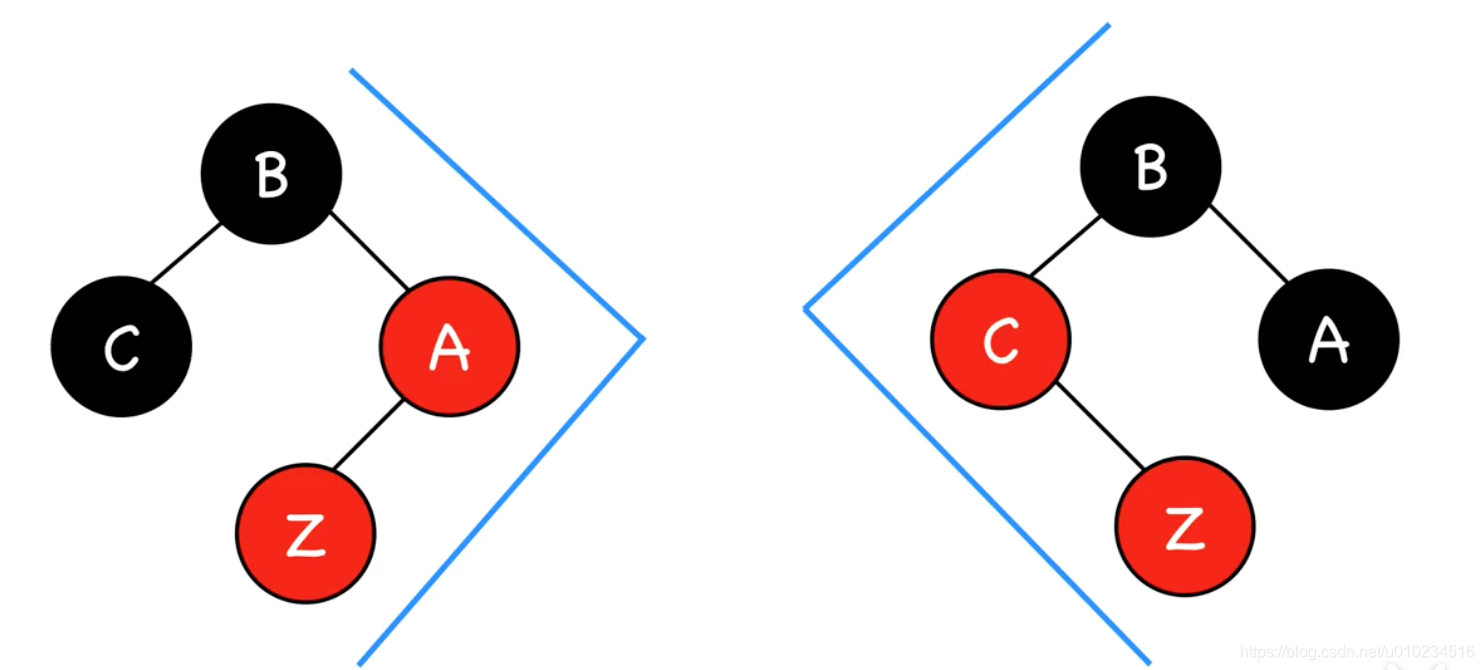
4. 插入节点的叔叔节点为黑色（直线式）
   
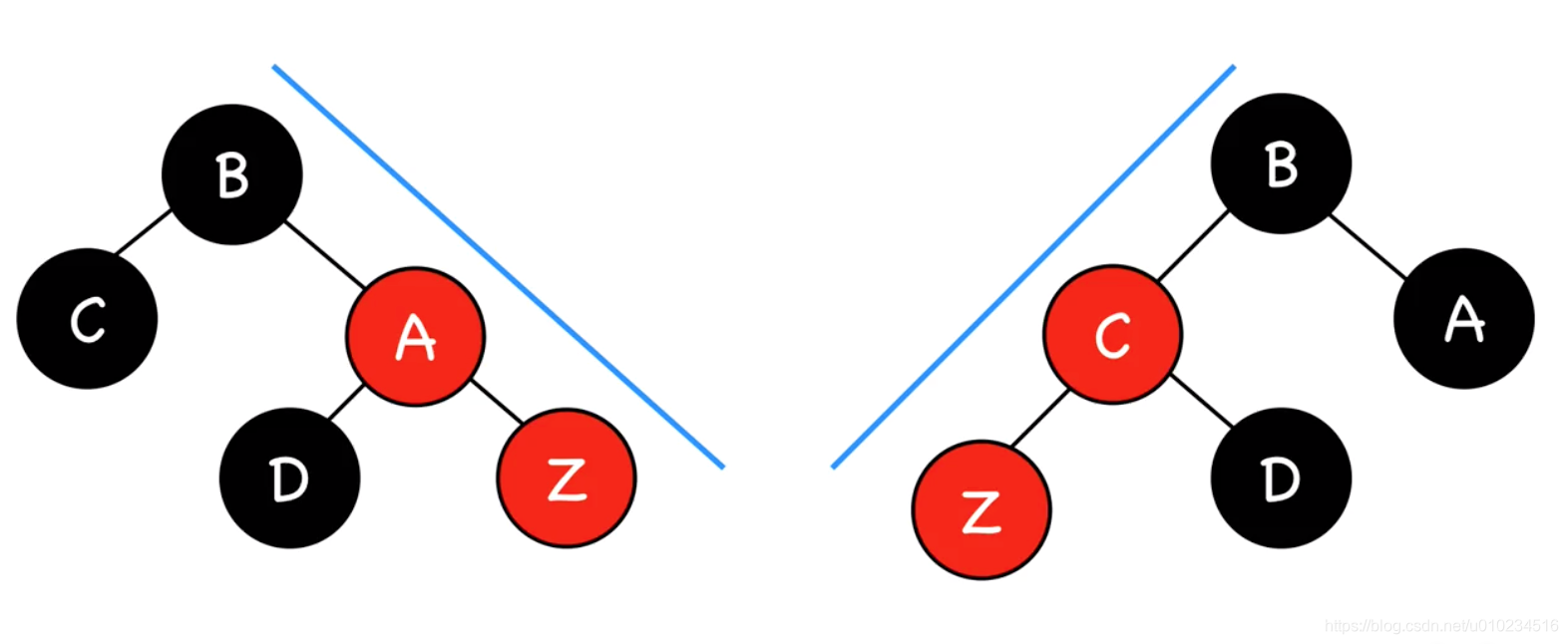
   所谓插入节点既可以是新插入的节点，也可以是经过其他修正方式产生的新的红色节点的子红色节点

红黑树的插入修正的4种方式

4种方式对应上述4中情况：

1. 将插入节点变为黑色，修正完成。
2. 将插入节点的父节点、叔叔节点变成黑色，祖父节点变成红色。将祖父节点作为新的插入节点（可能需要继续修正）。
3. 将插入节点的父节点进行旋转（方向为插入节点的反方向，例如插入节点为左子节点则右旋），转换为情况4。
4. 将插入节点的父节点变黑，祖父节点变红，祖父节点进行旋转（方向为插入节点的反方向，例如插入节点为左子节点则右旋），修正完成。

源码分析

源码摘自JDK1.8 java.util.HashMap.java 2219行

static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,TreeNode<K,V> x) {// 插入节点为红色x.red = true;for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {// 如果没有父节点，说明已经是根节点，染成黑色，修正完成（可能是插入了根节点，也可能是经过情况1的修正后）if ((xp = x.parent) == null) {x.red = false;return x;}// 如果父节点是黑色（无须修正的情况） 或者 不存在祖父节点（什么时候会走这个条件，还没搞懂，有懂的请指教）else if (!xp.red || (xpp = xp.parent) == null)return root;// 父节点是祖父节点的左孩子if (xp == (xppl = xpp.left)) {// 情况1if ((xppr = xpp.right) != null && xppr.red) {// 叔叔节点改成黑色xppr.red = false;// 父节点改成黑色xp.red = false;// 祖父节点改成红色xpp.red = true;// 插入节点指向祖父节点x = xpp;}else {// 情况3（插入节点是右孩子，插入节点的父亲是祖父的左孩子）if (x == xp.right) {// 插入节点是右孩子，所以左旋root = rotateLeft(root, x = xp);xpp = (xp = x.parent) == null ? null : xp.parent;}// 情况4if (xp != null) {// 父节点变黑xp.red = false;// 为什么要判空呢？理论上不可能有空的时候。// x只会代表一个红色节点（新插入的节点必然红色，否则方法已退出）// x的父节点一定是红色（如果是黑色，方法已经退出）// x一定有祖父节点（因为父节点一定是红色，那么红色节点一定有父节点，否则原来就不是红黑树）// 这里的疑问，有懂的欢迎留言解答下if (xpp != null) {// 祖父节点变红xpp.red = true;// 插入节点是左孩子（本来就是左或者经过上面的情况4处理变成左），右旋root = rotateRight(root, xpp);}}}}else {if (xppl != null && xppl.red) {xppl.red = false;xp.red = false;xpp.red = true;x = xpp;}else {if (x == xp.left) {root = rotateRight(root, x = xp);xpp = (xp = x.parent) == null ? null : xp.parent;}if (xp != null) {xp.red = false;if (xpp != null) {xpp.red = true;root = rotateLeft(root, xpp);}}}}}}

这篇关于jdk1.8 HashMap红黑树插入修正源码分析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---