Reinforcement Learning强化学习系列之一：model-based learning

本文主要是介绍Reinforcement Learning强化学习系列之一：model-based learning，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

在机器学习和深度学习坑里呆了有一些时日了，在阿里实习过程中，也感觉到了工业界和学术界的一些迥异，比如强化学习在工业界用的非常广泛，而自己之前没有怎么接触过强化学习的一些知识，所以感觉还是要好好的补一补更新一下自己的知识库，以免被AI时代抛弃。

强化学习初识

强化学习要素

强化学习可以用下面这张图表示：

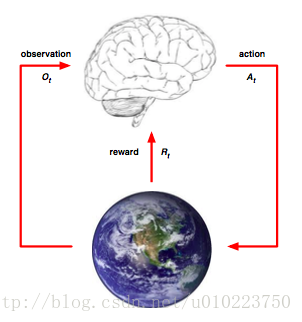
从上图可以看出，强化学习的要素是：
1. Agent（图中指大脑）
2. Environment（图中指地球）
在每个时间$t$内：
Agent做的事是：
1. 做出行动$A_t$
2. 观察环境$O_t$
3. 计算收益$Reward_t$

Environment做的事是：
1. 感知Agent的$A_t$
2. 做出环境反应$O_{t+1}$
3. 反馈收益$R_{t+1}$

因此强化学习其实是一个不断Agent与外界环境进行交互并产生新的行为的过程，而如何让行为得到最大的收益，这就是其学习过程。这里我使用【参考1】的强化学习任务要素：$E=<X,A,P,R>$，其中$X$指的是当前的环境状态，$A$是做出的行动，$P$是指从状态$X_t$执行行动$A_t$后到新的状态$X'$的转移概率矩阵，$R$指的是奖赏$reward$，而我们的学习目标就是，让agent学习出一个好的策略$policy$使得总体的期望$reward$最大。

具体概念性请参考【参考1】

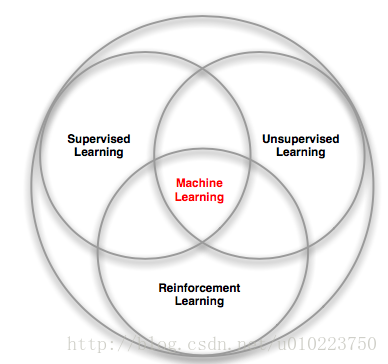
强化学习与监督学习

强化学习和有监督学习以及无监督学习的区别和联系可以用下图表示：

与有监督的学习差异

有监督的学习可以描述为你在学习过程中，有个老师在旁边教你怎么做，有着严格的标准，而强化学习则没有这个老师教，而且也没有固定的标准方法，其标准方法都是探索出来的。

与无监督的学习差异

强化学习看似是无监督学习，其实和无监督的学习差别较大，主要体现在几点：
1. 无监督的学习更多的是探索数据内部的存在规律或者联系，而强化学习主要探索的是策略方式
2. 强化学习和时间有很大的关系，而且反馈都是具有时间效应的，这点和无监督学习非常不一样

MDP过程

所谓MDP，即Markov Decison Process,具备马尔科夫链性质：系统下一时间的状态仅由当前时刻的状态决定；回到强化学习本省，其实就是下一个状态只由前一时刻的状态和Action决定，和历史的状态和Action无关。

这个性质非常重要，因为后面的很多推断都是依据这个性质推导出来的，了解HMM模型的人应该知道，马尔科夫链的这条性质是解码算法的根本。

有模型的学习：model-based learning

强化学习主要有 1）有模型的学习 2）无模型学习 3）值函数近似 4）模仿学习 等；本系列主要对前3种学习方法进行叙述

有模型和无模型的学习差异在于有模型的$E=<X,A,P,R>$都是已知的，而无模型的学习是$E=<X,A,P,R>$不一定可知；

对于有模型的学习基本的基础知识可以参看【参考1】的第16章的第3小节；这里我主要针对一个实际的问题，对其原理进行一个阐述；

问题描述

现有$N \times M$的二维矩阵，其$E=<X,A,P,R>$描述为：
$X$:其状态有2个终态，也就是图中的阴影部分，其他的都是非终态；
$A$:对于每个状态都有四个action，分别是上下左右
$P$：对于一个确定的状态$S$和一个动作$action$，其下一个状态一定是确定的，也就是转移概率为1
$R$:如果达到终态，其reward为0；否则为-1
任务：确定最佳的策略/Value function，使其期望reward最大

我们首先对任务进行建模：

#coding=utf-8
import numpy as np
"""
author:luchi
date:2017/9/2
description:gridworld environment
"""class GridWorldEnv(object):def __init__(self,shape=[4,4]):if not isinstance(shape, (list, tuple)) or not len(shape) == 2:raise ValueError('shape argument must be a list/tuple of length 2')self.nS = np.prod(shape)self.nA = 4 # four directionsMAX_X = shape[0]MAX_Y = shape[1]P={}grid = np.arange(self.nS).reshape(shape)it = np.nditer(grid,flags=['multi_index'])#move directionsUP = 0RIGHT = 1DOWN = 2LEFT = 3while not it.finished:state = it.iterindexx,y = it.multi_index# print state# print(x,y)P[state] = {a:[] for a in range(self.nA)}is_terminal_state = lambda state: state==0 or state==self.nS-1reward = lambda state : 0.0 if is_terminal_state(state) else -1.0if is_terminal_state(state):P[state][UP] = [(1.0,state,reward(state),True)]P[state][RIGHT] = [(1.0,state,reward(state),True)]P[state][DOWN] = [(1.0,state,reward(state),True)]P[state][LEFT] = [(1.0,state,reward(state),True)]else:Up_Grid = state if x==0 else state-MAX_YRight_Grid = state if y==MAX_Y-1 else state+1Down_Grid = state if x==MAX_X-1 else state+MAX_YLeft_Grid = state if y==0 else state-1P[state][UP] = [(1.0,Up_Grid,reward(Up_Grid),is_terminal_state(Up_Grid))]P[state][RIGHT] = [(1.0,Right_Grid,reward(Right_Grid),is_terminal_state(Right_Grid))]P[state][DOWN] = [(1.0,Down_Grid,reward(Down_Grid),is_terminal_state(Down_Grid))]P[state][LEFT] = [(1.0,Left_Grid,reward(Left_Grid),is_terminal_state(Left_Grid))]# print P[state]it.iternext()self.P = Pgrid = GridWorldEnv()

策略评估

策略评估是已知模型的参数的，对于一个策略，估计其期望累计奖赏，使用$discount$的计算方法，对于策略$\pi$,在时间$T$取得的预期收益$V_T^{\pi}(x)$计算方法如下：

$$V_T^{\pi}(x) = \sum_{a \in A}\pi(x,a)\sum_{x' \in X}P_{x \to x'}^a(R_{x \to x'}^{a}+\gamma V_{T-1}^{\pi}(x'))$$ 因此这是一个动态规划问题，对于 $t=0$初始化 $V_0^{\pi}(x)$为0，然后按照递推公式动态规划计算即可。

在本文的问题中，我们使用随机策略$random policy$作为我们的起始策略；这里随机策略指的是，对于一个状态$S$其$action$的所有概率都相等，也就是$uniform$分布，按照下面的方法计算其策略Value值：

def policy_evaluation(self,policy,env,discount_factor=1.0, theta=0.00001,max_iter_num=1000):delta =0.0V = np.zeros(env.nS)iter_count=0while True:new_V = np.zeros(env.nS)for s in range(env.nS):V_x = 0.0for idx,prob in enumerate(policy[s]):for trans_prob,next_state,reward,isFinite in env.P[s][idx]:V_x += prob*trans_prob*(reward+discount_factor*V[next_state])new_V[s]=V_xdelta = max(delta, np.abs(V_x - V[s]))iter_count+=1if delta<theta or iter_count>max_iter_num:breakelse:V = new_Vreturn np.array(V)

计算的$V$结果如下：

[[  0. -13. -19. -21.][-13. -17. -19. -19.][-19. -19. -17. -13.][-21. -19. -13.   0.]]

我们可以看到对于model-based 学习方法，其value值最终计算的能够逐步收敛，且反映了数据本身的特征。

策略改进算法

我们想得到一个$policy$能够使得期望的$V$最大，对于$|X|$个状态和$|A|$个动作，我们的策略就会有$|A|^{|X|}$个，这个计算开销显然太大；能不能有更简便的方法，答案是肯定的。

对于

$$V_T^{\pi}(x) = \sum_{a \in A}\pi(x,a)\sum_{x' \in X}P_{x \to x'}^a(R_{x \to x'}^{a}+\gamma V_{T-1}^{\pi}(x'))$$ 这个公式，如果对于 $T-1$时刻，我们已经取得了最优解，那么对于 $T$时刻，显然最优解就是：
$$V_T^{\pi}(x) = max_{a \in A}(\sum_{x' \in X}P_{x \to x'}^a(R_{x \to x'}^{a}+\gamma V_{T-1}^{\pi}(x')))$$ 也就是选择一个能获得最大的V的那个动作作为当下执行的动作即可。我们就可以获得最优状态-动作值函数: $$Q_{T}^*(x,a)=\sum_{x' \in X}P_{x \to x'}(R_{x \to x'}+\gamma max_{a' \in A}(Q_{T}^*(x',a')))$$
该式称之为最优 $Bellman$等式
那么由于整个递推过程都是递增的，那么对于当前的策略 $\pi$，可以放心的将其改为: $$\pi'(x)=argmax_{a \in A}Q^{\pi}(x,a)(1)$$ 直到 $\pi$与 $\pi'$不再发生变化，即找到最优策略。

结合前面2节，我们可以结合起来得到最优策略办法：

策略迭代

策略迭代思路是：从一个初始策略出发(一般是随机策略),先进行策略评估，然后进行策略改进，不断迭代直到策略收敛不再变化为止。
结合本例子，代码可编写如下：

def policy_iteration(self,policy,env,discount_factor=1.0):while True:V = self.policy_evaluation(policy,env)policy_stable = Truefor s in range(env.nS):policy_before = self.select_biggest(policy[s])action_values = np.zeros(env.nA)for a in range(env.nA):for trans_prob,next_state,reward,isFinite in env.P[s][a]:action_values[a]+=trans_prob*(reward+discount_factor*V[next_state])policy_cur = self.select_biggest(action_values)if not policy_before==policy_cur:policy_stable=Falsenew_policy = np.zeros(env.nA)for p in policy_cur:new_policy[p]=1.0/len(policy_cur)policy[s]=new_policyif policy_stable:return policy,V

迭代后的策略和值函数分别是：
策略，每行索引(0,1,2,3)分别表示（上，右，下，左），其值表示执行该动作的概率：

[[ 0.25  0.25  0.25  0.25][ 0.    0.    0.    1.  ][ 0.    0.    0.    1.  ][ 0.    0.    0.5   0.5 ][ 1.    0.    0.    0.  ][ 0.5   0.    0.    0.5 ][ 0.25  0.25  0.25  0.25][ 0.    0.    1.    0.  ][ 1.    0.    0.    0.  ][ 0.25  0.25  0.25  0.25][ 0.    0.5   0.5   0.  ][ 0.    0.    1.    0.  ][ 0.5   0.5   0.    0.  ][ 0.    1.    0.    0.  ][ 0.    1.    0.    0.  ][ 0.25  0.25  0.25  0.25]]

值函数：

[[ 0.  0. -1. -2.][ 0. -1. -2. -1.][-1. -2. -1.  0.][-2. -1.  0.  0.]]

我们把策略可视化可以得到策略如下：

从图中可以看到策略是有效的

值迭代

策略的改进和值的改进是一样的，因为可以将策略迭代换成值迭代，按照公式(1)的方法，每次选取值最高的策略作为当前的策略，代码如下：

    def value_iteration(self,env,theta=0.0001,discount_factor=1.0):V = np.zeros(env.nS)policy=np.zeros([env.nS,env.nA])while True:delta=0update_V=np.zeros(env.nS)for s in range(env.nS):V_x = np.zeros(env.nA)for a in range(env.nA):for trans_prob,next_state,reward,isFinite in env.P[s][a]:V_x[a]+=trans_prob*(reward+discount_factor*V[next_state])policy_cur = self.select_biggest(V_x)new_policy = np.zeros(env.nA)for p in policy_cur:new_policy[p]=1.0/len(policy_cur)policy[s]=new_policybestAction = np.max(V_x)update_V[s]=bestActiondelta = max(delta, np.abs(bestAction - V[s]))V = update_Vif delta<theta:breakreturn policy,V

迭代后的策略是：

[[ 0.25  0.25  0.25  0.25][ 0.    0.    0.    1.  ][ 0.    0.    0.    1.  ][ 0.    0.    0.5   0.5 ][ 1.    0.    0.    0.  ][ 0.5   0.    0.    0.5 ][ 0.25  0.25  0.25  0.25][ 0.    0.    1.    0.  ][ 1.    0.    0.    0.  ][ 0.25  0.25  0.25  0.25][ 0.    0.5   0.5   0.  ][ 0.    0.    1.    0.  ][ 0.5   0.5   0.    0.  ][ 0.    1.    0.    0.  ][ 0.    1.    0.    0.  ][ 0.25  0.25  0.25  0.25]]

值函数是：

[[ 0.  0. -1. -2.][ 0. -1. -2. -1.][-1. -2. -1.  0.][-2. -1.  0.  0.]]

可以看出的是，策略迭代和值函数迭代得到的结果是一样的。

后记

强化学习和机器学习的思路方法还是很不一样，对于未知的问题强化学习显然能够提供更好的解决方案

代码放在我的GitHub上，后续会陆续更新

【参考1】周志华《机器学习》
【参考2】从概念到应用，全面了解强化学习
【参考3】Learning Reinforcement Learning (with Code, Exercises and Solutions)

这篇关于Reinforcement Learning强化学习系列之一：model-based learning的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---