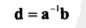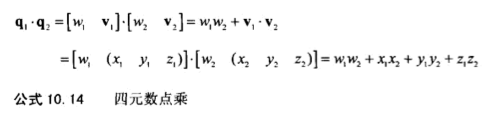本文主要是介绍3D数学基础--3D中的方位与角位移(2),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言:3D中讨论的四元数都是单位四元数
四元数记法
上一章节讲了用三个数表达3D方位一定会有万向锁这样的问题,它涉及到一些非常高级的数学概念,如“簇”。而四元数通过使用四个数来表达方位,从而可以避免这些问题,下面先来看看它的记法:

注:w:类似复数实部,v:虚数。
四元数的数学渊源
四元数其实是由数学里的复数引申而来的,首先来简单说下什么是复数?复数=实数+虚数,它扩展了如对一个负数开平方根的问题。下面来看看复数的定义:

复数集存在于一个2D平面上,这个平面有两个轴:实轴(x)和虚轴(y)。这样,就能将复数(x,y)解释为一个2D向量,好的,现在我们可以这样通俗的理解,复数=向量。下面再来看看用复数怎么表达平面中的旋转:
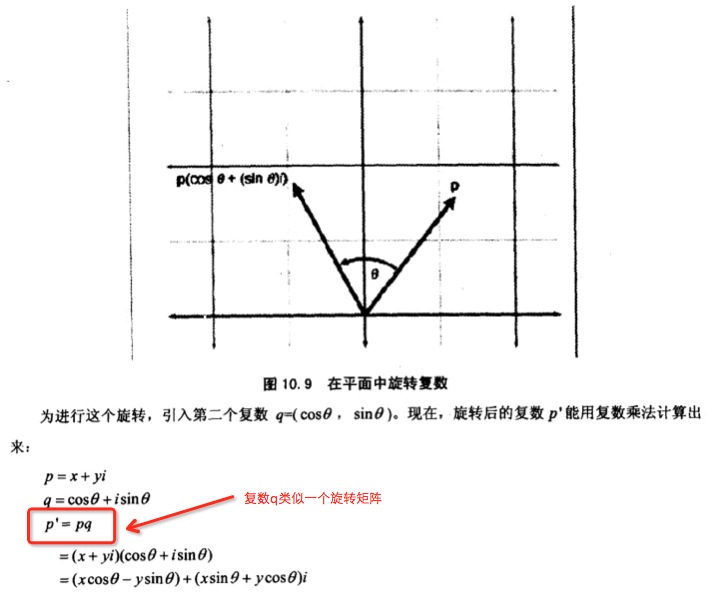
从上面可以看出引入复数q和用2×2旋转矩阵达到的效果是一样的,目前为止,我们已经将复数和前面学习的知识联系起来了,而现在我们讲的只是2D平面,那么怎么把复数扩展到3D中呢?它又怎么和四元数联系起来呢?下面我们来看下书上关于它的一个典故:

四元数扩展复数系统,它使用了三个虚部i, j, k。它们关系如下:
四元数几何意义
欧拉证明了一个旋转序列等价于单个旋转,因此,3D中的任意角位移都能表示为绕单一轴的单一旋转。我们记角度为θ,旋转轴为n(向量),那么绕n轴旋转θ角度,可用复数形式表示为(θ,n),那么其对应的四元数表示为:

注释:我们可以近似把一个四元数理解为一个旋转矩阵或角位移。
四元数的一般数学运算
负四元数:
q和-q代表的角位移是相同的,其实就是相当于将θ加上360°的倍数,对方位没影响。所以负四元数只是在数学上把它的四个分量都变负了,但几何上它们是等效的。即3D中任意角位移都有两种不同的四元数表示方法,它们互相为负。没有角位移的单位四元数:
注:代入上面四元数的四个值公式即可得出。四元数的模:
而我们3D数学里只使用模为1的四元数(单位四元数),即前面列出的四元数的四个值公式的四元数。四元数的共轭和逆:
数学定义我就直接拿书上讲的,如下:
由于我们只使用单位四元数,所以四元数的逆和共轭是相等的。那么,它们有什么几何意义呢?共轭其实就是把四元数的向量部分变负,所以一个四元数的共轭就是代表一个相反的角位移。
注释:其实我们还可以保持四元数向量部分不变,而让角度部分变负,同样能代表一个相反的角位移。但为了和复数的共轭概念一致,所以四元数的共轭用上面那种形式定义。四元数的叉乘:
四元数的叉乘不用乘号,而且行与列的形式也没什么区别,下面是四元数乘法的标准定义:
但我们实际不用这种形式,具体原因这里不打算详细讲解,大体是因为这个形式会导致多个变换连接成一个后,变换顺序会颠倒。以后会把这些数学计算封装成一个四元数的类,对于里面的数据我们不再需要管。之所以用叉乘就是执行旋转变换时需要用到它。四元数“差”:
四元数的差是指一个方位到另一个方位的角位移。我们用四元数表示是:从a旋转到b的角位移d等于:四元数点乘:
四元数的点乘和向量的点乘很类似,几何原理也类似,a·b的绝对值越大,a和b代表的角位移越“相似”。公式如下:
四元数的高级数学运算
四元数的对数,指数和标量乘运算:
虽然这些运算我们很少直接使用它们,但它们是某些重要四元数运算的基础,下面来分别看看它们的定义:
四元数求幂:
注意它与上面指数运算的区别,指数运算底数是e,而这里是四元数做底数。所以,指数运算只要一个参数–四元数,而四元数求幂要两个参数–四元数和指数。公式如下:
再来说说它能做什么用?假设,四元数q代表一个角位移,现在想要得到代表1/3这个角位移的四元数,其实就是等于这个四元数的1/3次幂。即四元数求幂它可以从角位移中抽取一部分。四元数求幂代码实例:
//四元数输入和输出float w, x, y, z;//指数float exponent;//检查单位四元数,避免除零if(fabs(w) < 0.9999f){//提取半角float alpha = acos(w);//计算新的alpha值float newAlpha = alpha * exponent;//计算新的w值w = cos(newAlpha);//计算新的x, y, z 值float mult = sin(newAlpha) / sin(alpha);x *= mult;y *= mult;z *= mult;}
四元数插值(slerp):
当今3D数学中四元数之所以存在的理由就是利用它可以在两个四元数间平滑的插值。它避免了欧拉角插值的所有问题。具体的推导过程就不详细解释了,有兴趣的可以自己查阅相关资料(3D数学基础图形与游戏开发),下面直接贴出公式:
slerp代码实例:
//两个输入四元数float w0, x0, y0, z0;float w1, x1, y1, z1;//插值变量float t;//输出四元数float w, x, y, z;//用点乘计算两四元数夹角的cos值float cosOmega = w0 * w1 + x0 * x1 + y0 * y1 + z0 * z1;//如果点乘为负,则反转一个四元数以取得短的4D弧if(cosOmega < 0.0f){w1 = -w1;x1 = -x1;y1 = -y1;z1 = -z1;cosOmega = -cosOmega;}//检查插值的起点和终点是否过于接近以避免除零float k0, k1;if(cosOmega > 0.9999f){//非常接近,直接用线性插值k0 = 1.0 - t;k1 = t;}else{//用三角公式sin^2(cosOmega) + cos^2(cosOmega) = 1计算出sinwfloat sinOmega = sqrt(1.0f - cosOmega * cosOmega);//通过sinw 和 cosw计算w夹角float omega = atan2(sinOmega, cosOmega);//计算分母的倒数,这样只需要一次除法float oneOverSinOmega = 1.0f / sinOmega;//计算插值变量k0 = sin((1.0f - t) * omega) * oneOverSinOmega;k1 = sin(t * omega) * oneOverSinOmega;}//得到插值w = w0 * k0 + w1 * k1;x = x0 * k0 + x1 * k1;y = y0 * k0 + y1 * k1;z = z0 * k0 + z1 * k1;- 四元数样条(squad):
slerp(球面线性插值)只提供了两个方位间的插值,但对于超过两个的方位序列,我们要进行插值就得用到squad。对于其具体数学原理推导这里也不打算讲了。
四元数的优点和缺点
四元数的一些其他角位移表示方法所没有的优点:
1,平滑插值
2,快速连接和角位移求逆,同样的操作,它要比矩阵快且容易些。
3,能快速转换成矩阵形式。
4,仅用四个数表示。缺点:
1,比欧拉角稍微大一些。
2,四元数可能不合法。因为我们讨论的有意义的四元数必须是单位大小,而输入坏数据或浮点数舍入误差累积都可能使四元数不合法(当然我们可以通过四元数标准化来解决这个问题)。
3,难于使用,在所有三种形式中,四元数是最难直接使用的。
这篇关于3D数学基础--3D中的方位与角位移(2)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!