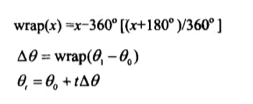3D数学基础--3D中的方位与角位移(1)

本文主要是介绍3D数学基础--3D中的方位与角位移(1)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

方位基本概念介绍

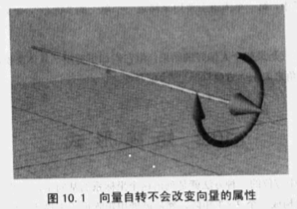
1，什么是方位？直观地说，方位主要描述的是物体的朝向。比如：我们知道的向量，它就只有方向但没有方位，因为它只有大小，而没有厚度和宽度，所以让向量自转其属性是不会发生任何变化的。然而，如果是一个物体，让它和向量一样自转，你会发现物体的朝向改变了，即方位发生了变化。示意图如下：
这里写图片描述

2，方位和角位移关系：我们知道不能用绝对坐标来描述物体的位置，要描述物体位置，必须把物体放在特定的参考系中(参考点)。同样，描述物体方位时，也不能使用绝对量，方位是通过相对已知方位的旋转来描述的。而这个旋转的量就称作角位移。在数学上，方位和角位移是等价的。但在概念上它们是有区别的，方位和角位移的区别就类似点和向量的区别一样。方位就只是直观地描述了方位，而角位移不仅描述了方位还描述了从源方位到新方位变换的过程(例如，从旧方位到新方位的角位移，或者从惯性坐标系到物体坐标系的角位移)。

3，总的来说，3D中描述物体方位的方法一般有3种：矩阵，欧拉角，四元数。而我们用矩阵和四元数来描述角位移，用欧拉角来描述方位。下面我们就来分别讲下矩阵，欧拉角，四元数的具体实现以及使用它们的优缺点。

矩阵形式

1，用矩阵描述方位其实就是用一个3 × 3的旋转矩阵来表示，这个矩阵的三行必须是基向量(单位向量且互相垂直)，对应着新坐标系的三个轴。

2，矩阵形式的优点：

可以立即进行向量的旋转(相乘即可)。
现在的图形API接口一般也是用的矩阵形式，所以如果你用的其他方式表示方位，在渲染管线的某处也要将其转换为矩阵形式。
多个角位移连接，如知道A相对于B的方位，又知道B相对于C的方位，可以直接使用矩阵表示出A相对于C的方位，即前面章节讲的矩阵的连接方法。
矩阵形式表示方位，很容易求它的逆矩阵，因为旋转矩阵是正交的，其逆矩阵只要简单的矩阵转置运算即可。

3，矩阵形式的缺点：

矩阵占用了更多的内存，3 × 3矩阵用9个数来保存方位，而实际上只需要3个数就能够确定了，特别是一些动画系统中，如骨骼动画就是通过控制父块和子块的相对方位来实现动作的，该模型假设被分解为15个块，每一帧为每一块保存一个方位，动画频率是15Hz，这就意味着每秒需要保存15×15=225个方位。使用矩阵形式，则每秒需要4×9×225=8100字节，而使用欧拉角，同样的数据只需4×3×225=2700字节。所以对于30s的动画数据，矩阵就比欧拉角多占用162K字节。
难于使用，不直观。人类考虑方位最直接的方式是角度，而矩阵使用的是向量。
矩阵可能是病态的，就是前面章节讲的正交矩阵，矩阵可能接受到坏数据。

欧拉角

1，什么是欧拉角？欧拉角将方位分解为绕三个互相垂直轴的旋转，只需三个角度值数据确定一个方位。而至于是绕哪三个轴，按什么顺序，旋转正方向等其实都是可以我们自己任意设定的，但一般有意义的设定是使用笛卡尔坐标系作为三个轴，旋转顺序使用“heading-pitch-bank”，即heading为绕y轴的旋转量，经过heading旋转后，pitch为绕x轴的旋转量，最后，经过了heading和pitch，bank为绕z轴的旋转量(绕的轴是物体坐标系轴而不是惯性坐标系轴)。旋转正方向一般使用左手法则确定。注意，上面说的“heading-pitch-bank”旋转顺序是针对物体从惯性坐标系到物体坐标系的变换(世界坐标系到物体坐标系的变换)，这种形式的变换开始时惯性坐标系和物体坐标系是重合的。而对于从物体坐标系到惯性坐标系的变换，这个旋转顺序是相反的，称作“roll-pitch-yaw”，roll类似bank，yaw类似heading。

2，欧拉角的优点：

欧拉角对于我们来说很容易使用，最为直观，数据就是角度值。
最为简洁，内存开销最小，只用三个数来表达方位。
任意三个数都是合法的，即没有不合法的欧拉角，当然数值可能不对，但至少它们是合法的。可矩阵和四元数就不一定是这样了。

3，欧拉角的缺点：

给定方位的表达方式不唯一，我们把其称为别名问题，具体原因是：1，角度天生存在周期性，将一个角度加上360°的倍数时，方位不会改变。2，三个角度不互相独立，如，pitch 135度等价于heading 180°，pitch 45°，然后bank 180°。所以为了解决上面说的同一个方位表达方式不唯一的情况，我们可以限定角度范围，即heading和bank限定在-180°到+180°之间，pitch限定在-90°到+90°之间。这样，在限定范围内，就只存在一个欧拉角描述某个方位了。事实上，还存在一个违反唯一性的情况：先heading 45°再pitch 90°，这与先pitch 90°再bank 45°是等价的。即只要pitch = ±90°时，heading-pitch与pitch-bank等效，我们称这种为万向锁。为了消除这个别名问题，我们一般规定如果pitch = ±90°时，则bank为零。
两个角度间求插值非常困难，先来说说什么是插值，插值其实就是指给你一个起点A和终点B，那么从A运动到B的轨迹是需要计算的，即A,B之间临时点的计算就是插值。再来看下书上的解释：

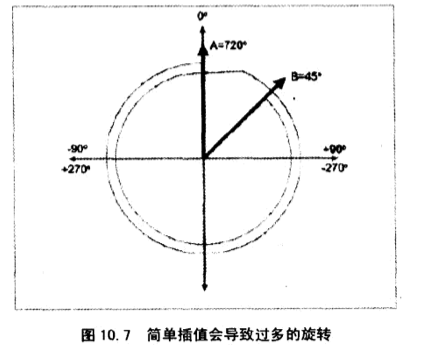
其实上面的插值计算就还有很多问题：第一，如果没有限制欧拉角，将得到很大的角度差。如下面A,B两个方位，其实它们只相差45°，但插值会在错误的方向上绕将近两周。

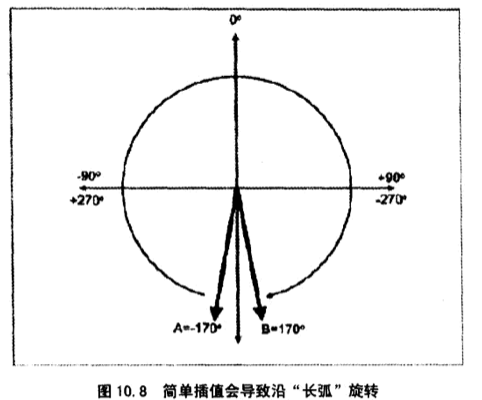
当然这种问题只要限制欧拉角范围就可以避免了。但插值还会有另外一个问题，这个问题是由于旋转角度的周期性引起的。如A的heading为-170°，B的heading为170°。这两个值只相差20°，但插值操作会错误的走’长弧’，绕了340°而不是更短的20°。如下图所示：

当然这个问题也是可以解决的，我们可以自己求得最短的弧，公式如下：

上面的两类问题，我们都可以解决，不过插值还有一个最坑的问题，是属于底层问题，至今都没有简单的解决方案–万向锁问题。这个问题会导致抖动，路径错误等现象，根本原因是由于插值过程中角速度不是恒定的。这是一个用三个数表达3D方位的方法与生俱来的问题，我们可以改变问题，但不能消灭它，任何使用三个数来表达3D方位的系统，如能保证空间的唯一性，就都会遇到这些问题。我们将在下一章节讲怎么用四元数解决这些问题。