本文主要是介绍【强化学习】公平性Actor-Critic算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Bringing Fairness to Actor-Critic Reinforcement Learning for Network Utility Optimization 阅读笔记
- Problem Formulation
- Learning Algorithm
- Learning with Multiplicative-Adjusted Rewards
- Solving Fairness Utility Optimization
- Evaluations
在网络优化问题中,公平性(fairness)是一个重要的考虑指标。随着越来越多的设备接入网络中,网络中的资源分配、任务调度等需要充分考虑设备之间的公平性,在系统效率与用户公平性之间达到一种平衡。近年来,强化学习被成功应用于网络优化问题的在线决策中,然而大部分算法聚焦于最大化所有agent的长期收益,很少考虑公平性。在这样的背景下,作者提出了一种fairness Actor-Critic algorithm,该算法将公平性融入到AC算法的设计中,旨在优化整体公平效用函数。具体做法为,设计了一种适应性奖励,在原奖励的基础上乘以一个权重,该权重与效用函数和过去的奖励有关。实验部分,作者将算法用于求解网络调度问题(convex)与视频流QoE优化问题(non-convex),说明了算法的有效性。
Problem Formulation
考虑一个网络效用优化问题,网络建模为环境,用户是agents,agent与环境进行交互,学习策略来优化rewards(如数据率等)。假设有K个agents,使用随机策略(stochastic policy) π \pi π(a|s)表示状态s下选择动作a的概率。 x π , k x_{\pi,k} xπ,k代表agent k在策略 π \pi π下的平均奖励
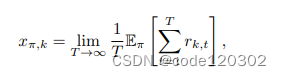
在本文中,使用 α \alpha α-fiar 效用函数,该函数广泛应用于网络优化领域。对于任意的 α \alpha α >= 0,有
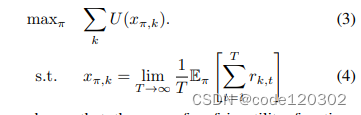
Learning Algorithm
假定在任何策略下的马尔科夫链都是不可还原/非周期性的。
Learning with Multiplicative-Adjusted Rewards
为了优化公平效用,在算法中需要追踪历史reward。为什么能使用过去历史reward来实现公平呢?
假设这样一个场景,两个agent分别有自己的reward,在某个策略下,如果截至到epoch t时agent 1比agent 2获得了更多的累积奖励,那么我们需要偏好使用策略梯度更新agent 2而不是agent 1。因此过去历史reward能够用于优化公平性。
使用 h π , t h_{\pi, t} hπ,t表示截止epoch t从采样路径中获得的数据,使用一个一致连续函数( uniformly-continuous function) ϕ ( h π , t ) \phi(h_{\pi, t}) ϕ(hπ,t)计算奖励的乘子。一致连续函数本身是“公平性”的体现。定义适应性奖励(adjust rewards)为
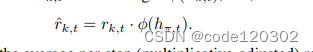
使用 ρ π ^ \hat{\rho_{\pi}} ρπ^表示MDP下平均单步适应性奖励,定义状态价值函数和动作价值函数如下:
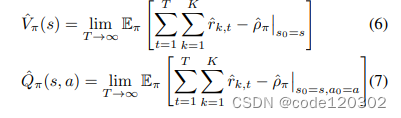
可以看到,V和Q都是有边界的。定义一个增强函数
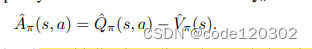
因为适应性奖励依赖于过去的历史h,所以标准RL的策略梯度理论不再适用适应性奖励。重新分析MDP。

当策略参数发生微小改变,平均奖励的改变如上式。
证明:定义新的状态 z t = [ s t , h π , t ] z_t = [s_t, h_{\pi, t}] zt=[st,hπ,t],新的马尔可夫过程为状态 z t z_t zt、动作 a t a_t at和奖励 r k , t ^ \hat{r_{k,t}} rk,t^的链。使用 p z z ′ a p^a_{zz'} pzz′a表示状态转移概率, V π ( z ) V_{\pi}(z) Vπ(z)和 Q π ( z , a ) Q_{\pi}(z,a) Qπ(z,a)为状态-值函数、动作-值函数。用 P π ( z ∣ s ) P^{\pi}(z|s) Pπ(z∣s)表示对于给定的状态s发生z的有限概率。Q函数与V函数表示如下
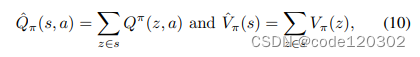
定义一个辅助函数
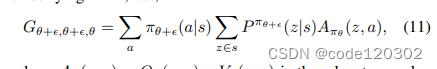
其中 A π ( z , a ) = Q π ( z , a ) − V π ( z , a ) A_{\pi}(z,a) = Q_{\pi}(z,a) - V_{\pi}(z,a) Aπ(z,a)=Qπ(z,a)−Vπ(z,a)。则有
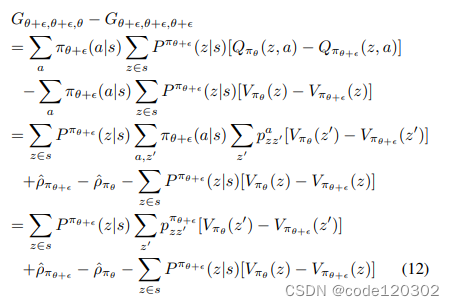
因为 ∑ a π ( a ∣ s ) Q π ( z , a ) = V π ( z ) \sum_{a}\pi(a|s)Q_{\pi}(z,a) = V_{\pi}(z) ∑aπ(a∣s)Qπ(z,a)=Vπ(z), 所以根据推导,有 G θ + ϵ , θ + ϵ , θ + ϵ G_{\theta+\epsilon, \theta+\epsilon, \theta+\epsilon} Gθ+ϵ,θ+ϵ,θ+ϵ = 0 。上述推导的最后一步中,第一项和第三项能够消掉,最后得到
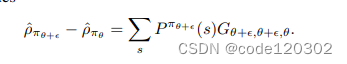
当策略参数发生的改变 ϕ \phi ϕ十分微小,策略 π θ \pi_{\theta} πθ的相应改变可以用 ϵ ∇ π θ ( a ∣ s ) + O ( ∣ ∣ ϵ ∣ ∣ 2 2 ) \epsilon \nabla \pi_{\theta}(a|s) + O(||\epsilon||^2_2) ϵ∇πθ(a∣s)+O(∣∣ϵ∣∣22)来bound。那么有


以上的梯度和较小的学习率能够使得算法收敛到一个平稳点。
策略梯度算法如下:(类似于REINFORCE算法)

Solving Fairness Utility Optimization
Lemma 2说明了新的策略梯度算法能收敛到适应性MDP的平稳点。定义最优策略的参数为 θ ∗ \theta^* θ∗,那么初始奖励的单步平均值为
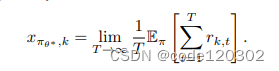
我们需要证明 θ ∗ \theta^* θ∗也是优化问题 ∑ k U ( x π θ , k ) \sum_{k}U(x_{\pi_{\theta},k}) ∑kU(xπθ,k)的平稳点。
对于一致连续函数 ϕ \phi ϕ,设定为效用函数U的一阶导数。该函数是符合Lipschitz连续的,有 ∣ U ′ ( x ) − U ′ ( y ) ∣ < = L ∣ x − y ∣ |U'(x) - U'(y)| <= L|x - y| ∣U′(x)−U′(y)∣<=L∣x−y∣, 对于L > 0。那么适应性奖励可以表示为
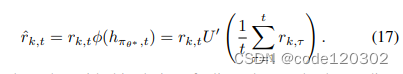

理论1:策略梯度算法能够收敛至公平效用函数的平稳点。
证明:由上已知, θ ∗ \theta^* θ∗是适应性MDP的平稳点,即 ∇ θ ρ π θ ^ ∣ θ = θ ∗ = 0 \nabla_{\theta} \hat{\rho_{\pi_{\theta}}} |_{\theta=\theta^* }= 0 ∇θρπθ^∣θ=θ∗=0,需要证明 θ ∗ \theta^* θ∗也是 α \alpha α-fair 效用函数 ∑ k U ( x π θ , k ) \sum_{k} U(x_{\pi_{\theta},k}) ∑kU(xπθ,k)的平稳点,也即 ∇ θ [ ∑ k U ( x π θ , k ) ] ∣ θ = θ ∗ = 0 \nabla_{\theta} [\sum_{k} U(x_{\pi_{\theta},k})] |_{\theta=\theta^* }= 0 ∇θ[∑kU(xπθ,k)]∣θ=θ∗=0。
所以我们需要分析单步平均适应性奖励 ρ π θ ^ \hat{\rho_{\pi_{\theta}}} ρπθ^和单步平均奖励 x π θ , k x_{\pi_{\theta},k} xπθ,k的关系
根据公式(17),有
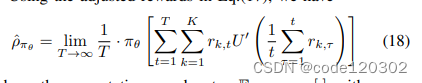
在policy π θ \pi_{\theta} πθ下,对于任意的 ϵ \epsilon ϵ > 0 存在一个足够大的T使得, ∣ 1 / T ∑ t = 1 T r k , t − x π θ , k ∣ < ϵ |1/T \sum^{T}_{t=1} r_{k,t} - x_{\pi_{\theta},k}| < \epsilon ∣1/T∑t=1Trk,t−xπθ,k∣<ϵ,结合U’的Lipschitz continuity有
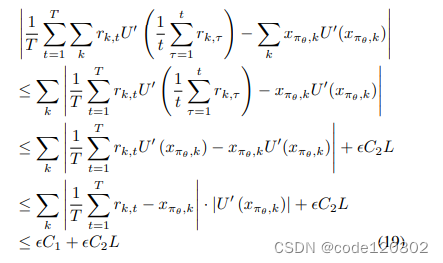
其中C1是 ∣ U ′ ( x π θ , k ) ∣ |U'(x_{\pi_{\theta},k})| ∣U′(xπθ,k)∣的边界,C2是 ∣ 1 / T ∑ t = 1 T r k , t ∣ |1/T \sum^{T}_{t=1} r_{k,t}| ∣1/T∑t=1Trk,t∣的边界。当T足够大,有
ρ π θ ^ = ∑ k x π θ , k U ′ ( x π θ , k ) \hat{\rho_{\pi_{\theta}}} = \sum_{k} x_{\pi_{\theta},k}U'(x_{\pi_{\theta},k}) ρπθ^=∑kxπθ,kU′(xπθ,k)
由于 θ ∗ \theta^* θ∗是适应性MDP的平衡点,有 ∇ θ [ x π θ , k U ′ ( x π θ , k ) ] ∣ θ = θ ∗ = 0 \nabla_{\theta} [x_{\pi_{\theta},k}U'(x_{\pi_{\theta},k})] |_{\theta=\theta^* }= 0 ∇θ[xπθ,kU′(xπθ,k)]∣θ=θ∗=0,也即 ∇ θ ρ π θ ^ ∣ θ = θ ∗ = 0 \nabla_{\theta} \hat{\rho_{\pi_{\theta}}} |_{\theta=\theta^* }= 0 ∇θρπθ^∣θ=θ∗=0。
上述证明结果可以形成一个新的actor-critic算法,使用 V w ^ ( s t ) \hat{V_{w}}(s_{t}) Vw^(st)作为神经网络近似state-value function,使用TD误差来训练 V w ^ ( s t ) \hat{V_{w}}(s_{t}) Vw^(st)。

Evaluations
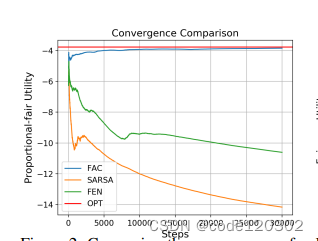
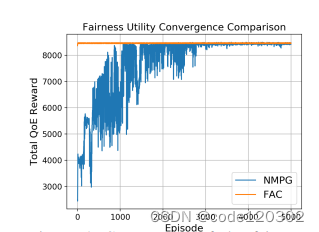
两个场景:无线网络调度和QoE优化
结果都表明FAC算法的优势:能够优化全局的效用、收敛速度快。
————————————————————————————
参考文献:
【1】J. Chen, Y. Wang and T. Lan, “Bringing Fairness to Actor-Critic Reinforcement Learning for Network Utility Optimization,” IEEE INFOCOM 2021 - IEEE Conference on Computer Communications, Vancouver, BC, Canada, 2021, pp. 1-10
这篇关于【强化学习】公平性Actor-Critic算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









