深度集成估计：简单且可扩展的不确定性预测

本文主要是介绍深度集成估计：简单且可扩展的不确定性预测，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

简介

深度神经网络(NNs)是强大的黑匣子预测器，最近在广泛的任务中取得了令人印象深刻的表现。量化神经网络中的预测不确定性是一个具有挑战性且尚未解决的问题。学习权重分布的贝叶斯神经网络是目前估计预测不确定性的最先进方法;然而，这些需要对训练过程进行重大修改，并且与标准(非贝叶斯)神经网络相比，计算成本很高。我们提出了一种替代贝叶斯神经网络的方法，它易于实现，易于并行化，只需要很少的超参数调优，并产生高质量的预测不确定性估计。通过对分类和回归基准的一系列实验，我们证明我们的方法产生了校准良好的不确定性估计，与近似贝叶斯神经网络一样好或更好。为了评估对数据集移位的鲁棒性，我们评估了已知分布和未知分布的测试样例的预测不确定性，并表明我们的方法能够在分布外的样例上表达更高的不确定性。我们通过在ImageNet上评估预测不确定性来证明我们方法的可扩展性。

论文：NeurIPS 2017
Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles
作者：
DeepMind
Balaji Lakshminarayanan Alexander Pritzel Charles Blundell

摘要

评估预测不确定性的质量是具有挑战性的，因为通常无法获得“真实的”不确定性估计。在这项工作中，我们将重点关注由神经网络的实际应用驱动的两种评估方法。首先，我们将检查校准[12,13]，这是一种频率论的不确定性概念，它测量主观预测和(经验)长期频率之间的差异。校准的质量可以通过适当的评分规则来衡量[17]，如对数预测概率和Brier评分[9]。请注意，校准与精度是正交关系:网络的预测可能是准确的，但可能是校准错误的，反之亦然。我们考虑的预测不确定性质量的第二个概念涉及预测不确定性到域移位的泛化(也称为分布外示例[23])，即测量网络是否知道它所知道的。例如，如果在一个数据集上训练的网络在一个完全不同的数据集上进行评估，那么网络应该输出高预测不确定性，因为来自不同数据集的输入将远离训练数据。校准良好的预测对模型错误规范和数据集移动具有鲁棒性，具有许多重要的实际用途(例如，天气预报、医疗诊断)。

最近有很多人对调整神经网络以包含不确定性和概率方法感兴趣。这项工作的大部分是围绕贝叶斯形式[4]展开的，即在神经网络的参数上指定先验分布，然后在给定训练数据的情况下，计算参数上的后验分布，用于量化预测的不确定性。由于精确贝叶斯推理对于神经网络来说在计算上是难以处理的，因此已经开发了各种近似方法，包括拉普拉斯近似[40]，马尔可夫链蒙特卡罗(MCMC)方法[46]，以及最近关于变分贝叶斯方法[6,19,39]，假设密度滤波[24]，期望传播[21,38]和随机梯度MCMC变体，如Langevin扩散方法[30,59]和哈密顿方法[53]。使用贝叶斯神经网络获得的预测不确定性的质量主要取决于(i)由于计算约束而产生的近似程度，以及(ii)先验分布是否“正确”，因为方便先验可能导致不合理的预测不确定性[50]。在实践中，与非贝叶斯神经网络相比，贝叶斯神经网络通常更难实现，训练速度也更慢，这就需要一种“通用解决方案”，既能提供高质量的不确定性估计，又只需要对标准训练管道进行微小的修改。

最近，Gal和Ghahramani[15]提出使用蒙特卡罗dropout (MC-dropout)在测试时使用dropout[54]来估计预测不确定性。已经有关于dropout的近似贝叶斯解释[15,29,41]的工作。MC-dropout的实现相对简单，因此在实践中很受欢迎。有趣的是，dropout也可以解释为集成模型组合[54]，其中预测在神经网络的集成上平均(参数共享)。集合解释似乎更合理，特别是在dropout率没有基于训练数据进行调整的情况下，因为任何对真实贝叶斯后验分布的合理近似都必须依赖于训练数据。这种解释激发了对集成的研究，作为估计预测不确定性的替代解决方案。

长期以来，人们一直观察到模型集成可以提高预测性能(参见[14]进行综述)。然而，何时以及为什么神经网络的集合可以预期产生良好的不确定性估计并不明显。贝叶斯模型平均(BMA)假设真实模型位于先验的假设类内，并进行软模型选择，在假设类内寻找单个最佳模型[43]。相反，集成执行模型组合，即。他们将这些模型结合起来，得到一个更强大的模型;当真实模型不在假设类内时，可以期望集成更好。我们参考[11,43]和[34，§2.5]进行相关讨论。重要的是要注意，即使是精确的BMA也不能保证对有关域移位的错误规范具有鲁棒性。

贡献总结:我们在本文中的贡献有两个方面。首先，我们描述了一种简单且可扩展的方法来估计神经网络的预测不确定性估计。我们主张使用适当的评分规则作为训练标准来训练概率神经网络(对预测分布进行建模)。我们还研究了两种修改对训练管道的影响，即(i)集成和(ii)对抗训练[18]，并描述了它们如何产生平滑的预测估计。其次，我们提出了一系列评估预测不确定性估计质量的任务，包括对监督学习问题中未知类的校准和泛化。我们表明，我们的方法明显优于(或匹配)MC-dropout。这些任务，以及我们简单而强大的基线，作为比较使用不同贝叶斯/非贝叶斯/混合方法获得的预测不确定性估计的有用基准。

新颖性和意义:神经网络的集成，或简称深度集成，已成功用于提高预测性能(例如ImageNet或Kaggle竞赛中的分类准确性)，对抗训练已用于提高对对抗示例的鲁棒性。然而，据我们所知，我们是第一个研究它们对预测不确定性估计的有用性的工作，并将它们的性能与当前最先进的近似贝叶斯方法在一系列分类和回归基准数据集上的性能进行比较。与贝叶斯神经网络(例如变分推理或MCMC方法)相比，我们的方法更容易实现，需要对标准神经网络进行很少的修改，并且非常适合分布式计算，从而使其对大规模深度学习应用具有吸引力。为了证明我们方法的可扩展性，我们在ImageNet上评估了预测的不确定性(据我们所知，我们是第一个这样做的)。大多数关于深度学习中不确定性的研究都集中在贝叶斯深度学习上;我们希望我们的方法的简单性和强大的经验性能将激发更多的非贝叶斯方法用于预测不确定性估计的兴趣。

深度集成：预测不确定性估计的简单方法

我们假设训练数据集D由N个数据点D = {xn,yn}N =1组成，其中x 有D维特征。对于分类问题，假设标签是K个类中的一个，即y 在{1，…K}中。对于回归问题，假设标签是实值。给定输入特征x，我们使用神经网络对标签上的概率预测分布p(y|x)进行建模，其中包括神经网络的参数。我们建议一个简单的方法:(1)使用适当的评分规则作为训练标准，(2)使用对抗性训练[18]来平滑预测分布，(3)训练一个集合。设M表示集合中nn的个数。我们首先描述如何训练单个神经网络，然后解释如何训练一个神经网络集合。

适当的评分规则

评分规则测量预测不确定性的质量(参见[17]的回顾)。评分规则为预测分布p(y|x)分配一个数值分数，奖励更好的校准预测。我们将考虑分数规则，分数越高越好。设评分规则为一个函数S(p，(y, x))，它评估相对于事件y|x ~q(y|x)的预测分布p(y|x)的质量，其中q(y, x)表示(y, x)元组上的真实分布。期望的评分规则是S(p，q)= R q(y, x)S(p，(y, x))dydx。一个适当的评分规则是S(p，q)<= S(q, q)具有相等当且仅当p(y|x)= q(y|x)，对于所有p和q。然后可以根据测量来训练神经网络，通过最小化损失L=-S(p，q)来鼓励校准预测不确定性。

结果表明，许多常见的神经网络损失函数都是合适的评分规则。例如，当似然最大化时，分数函数是S(p，(y, x)) = log p(y|x)，这是一个合理的评分规则，因为Gibbs不等式:S(p，q)= Eq(x)q(y|x)log p(y|x) Eq(x)q(y|x)log q(y|x)。在多类K-way分类中，流行的softmax交叉熵损失相当于对数似然，是一种合适的评分规则。有趣的是，L= -S(p，(y, x)) ，将标签的预测概率与正确标签的单次编码之间的平方误差最小化，也是一种合适的评分规则，称为Brier评分[9]。这为通过最小化二元标签与其相关概率之间的平方误差来训练神经网络的常见技巧提供了理由，并表明它实际上是具有理想属性的定义良好的损失。

回归训练校准

对于回归问题，神经网络通常输出单个值，例如µ(x)，并优化参数以最小化训练集上的均方误差(MSE)。然而，MSE并没有捕捉到预测的不确定性。Follow [47]，我们使用一个在最后一层输出两个值的网络，对应于预测的平均值µ(x)和variance2 > 0。通过将观测值视为具有预测均值和方差的(异方差)高斯分布的样本，我们最小化负对数似然准则:
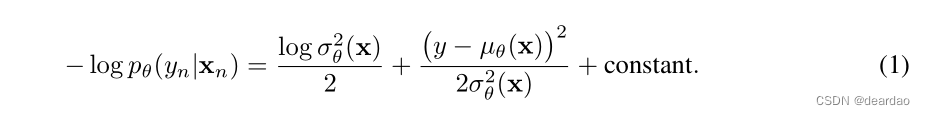
在这里插入图片描述
在实验中，我们发现上述方法的效果令人满意。然而，两个简单的扩展值得进一步研究:(i)对μ(x)和variance的最大似然估计可能过拟合;可以施加先验并执行最大后验(MAP)估计。(ii)在高斯分布过于严格的情况下，可以使用复杂分布，例如混合密度网络[5]或重尾分布。

对抗性训练平滑预测分布

由Szegedy等人[55]提出并由Goodfellow等人[18]扩展的对抗性示例是那些与原始训练示例“接近”的示例(例如，视觉上无法与原始图像区分的图像)，但被NN错误分类。Goodfellow等人[18]提出了快速梯度符号法作为生成对抗性示例的快速解决方案。给定目标为y的输入x和loss ( $\theta$ ，x,y)，快速梯度符号法生成一个对抗性的例子，如x0 = x + $\epsilon \Delta_x$ ，其中的一个小值，使得扰动的最大范数有界。直观地，对抗性扰动通过沿网络可能增加损失的方向添加扰动来创建新的训练样例。假设样本足够小，这些对抗性样本可用来扩充原始的训练集，将(x0,y)作为额外的训练样本。这一过程被称为对抗训练，3被发现可以提高分类器的鲁棒性[18]。

有趣的是，对抗性训练可以被解释为一种计算效率高的解决方案，通过增加目标在观察到的训练样本的一个邻域附近的可能性，来平滑预测分布。理想情况下，人们希望沿{1，-1} $^D$ 的所有2D方向平滑预测分布;然而，这在计算上是昂贵的。随机方向不一定会增加损失;然而，对抗性训练根据定义计算损失高的方向，因此比平滑预测分布的随机方向更好。Miyato等人[44]提出了一个相关的想法，称为虚拟对抗训练(VAT)，他们选择x =arg max KL p(y|x)||p(y|x + x); VAT的优点是它不需要知道真实目标y，因此可以应用于半监督学习。Miyato等人[44]表明，使用VAT的分布平滑有利于有效的半监督学习;相反，我们研究了对抗性训练在预测不确定性估计中的使用。因此，我们的贡献是互补的；可以使用VAT或其他形式的对抗性训练，参见[33]，以改善半监督设置中的预测不确定性。

整体:训练和预测

最流行的集成是使用决策树作为基础学习器，并且在集成的文献中已经探索了各种各样的方法。总的来说，集成有两类:基于随机化的方法，如随机森林[8]，其中集成成员可以在没有任何交互的情况下并行训练，以及基于增强的方法，其中集成成员是顺序拟合的。我们只关注基于随机化的方法，因为它更适合分布式并行计算。Breiman[8]表明随机森林的泛化误差可以用单个树之间的强度和相关性的函数作为上界;因此，希望使用随机化方案，使单个模型的预测去相关，并确保单个模型是强的(例如，高精度)。其中一种流行的策略是bagging(又名bootstrapping)，即在原始训练集的不同bootstrap样本上训练集合成员。如果基础学习器缺乏内在的随机化(例如，它可以通过解决凸优化问题来有效地训练)，套袋是诱导多样性的良好机制。然而，如果底层基础学习器有多个局部最优，就像神经网络的典型情况一样，自举有时会损害性能，因为在自举样本上训练的基础学习器只能看到63%的唯一数据点在决策树集成的文献中，Breiman[8]提出将bagging[7]与每个节点的特征随机子集选择相结合。Geurts等人[16]后来表明，如果可以在随机子集选择过程中注入额外的随机性，套袋是不必要的。直观地说，使用更多的数据来训练基础学习器有助于减少它们的偏差，而集成有助于减少方差。

我们使用整个训练数据集来训练每个网络，因为深度nn通常在数据更多的情况下表现得更好，尽管如果需要的话，使用随机子样本也很简单。我们发现神经网络参数的随机初始化，以及数据点的随机洗牌，足以在实践中获得良好的性能。在我们的实验中，我们观察到装袋会降低性能。Lee等人[36]独立观察到，在整个数据集上随机初始化的训练优于深度集成的bagging

在这里插入图片描述

实验结果

对于分类和回归，我们评估了依赖于预测不确定性的负对数似然(NLL)。NLL是一种合适的评分规则，也是评估预测不确定性的常用指标[49]。对于分类，我们还测量分类准确性和Brier评分。对于回归问题，我们还测量了均方根误差(RMSE)。除非另有说明，我们在实验中使用batch size为100和Adam optimizer，固定学习率为0.1。我们使用相同的技术为回归问题生成对抗性训练示例。Goodfellow等人[18]对所有维度使用了一个固定的杯子;如果输入维度有不同的范围，这是不令人满意的。因此，在我们所有的实验中，我们将其设为该特定维度上训练数据范围的0.01倍。我们在Torch中使用默认的权重初始化。
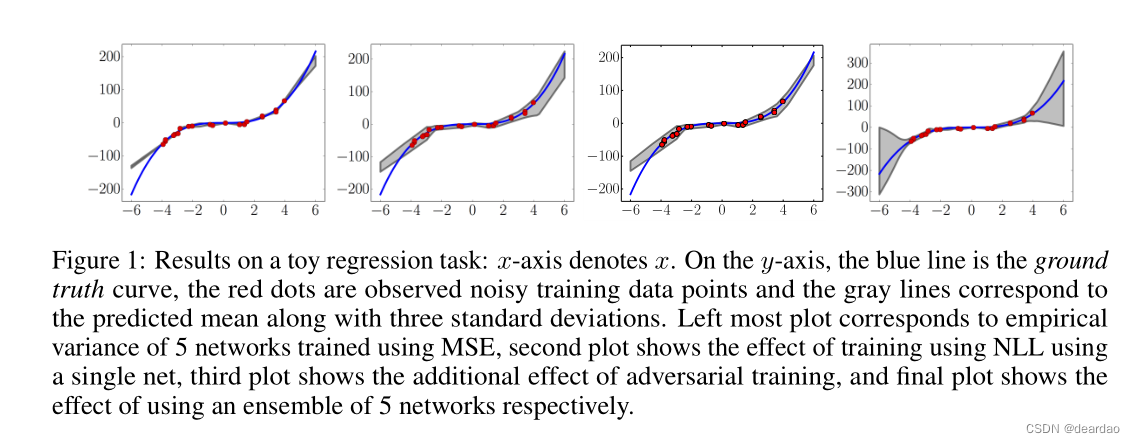
在这里插入图片描述
在我们的下一个实验中，我们将我们的方法与在回归任务中使用神经网络进行预测不确定性估计的最先进方法进行比较。我们使用Hernandez- Lobato和Adams[24]提出的实验设置来评估概率反向传播(PBP)，其也没用于评估MC-Dropout。

每个数据集被分成20个训练-测试Set，除了蛋白质数据集使用5个折叠和年份预测MSD数据集使用单个训练-测试分割。我们使用相同的网络架构:具有ReLU非线性的1隐藏层神经网络[45]，对于较小的数据集包含50个隐藏单元，对于较大的蛋白质和年份预测MSD数据集包含100个隐藏单元。我们训练了40个时代;关于数据集和实验方案的更多细节，我们参考[24]。我们在合奏中使用了5个网络。我们的结果显示在表1中，以及各自论文中报告的PBP和MC-dropout结果。
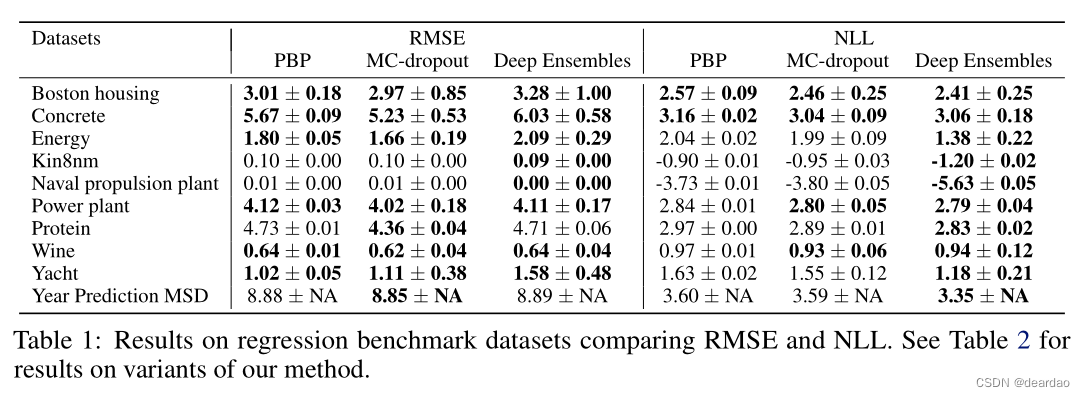
在这里插入图片描述
我们观察到，我们的方法在NLL方面优于(或与)现有方法。在一些数据集上，我们观察到我们的方法在RMSE方面稍微差一些。我们认为这是因为我们的方法针对NLL(捕获预测不确定性)而不是MSE进行了优化。附录A.1中的表2报告了我们方法变体的其他结果，展示了使用集成和学习方差的优势。

分类

接下来，我们使用MNIST和SVHN数据集评估分类任务的性能。我们的目标不是在这些问题上实现最先进的性能，而是评估对抗性训练的效果以及集合中网络的数量。为了验证对抗性训练是否有帮助，我们还包括一个基线，它选择一个随机的有符号向量。对于MNIST，我们使用具有3个隐藏层的MLP，每层有200个隐藏单元，以及具有批处理归一化的ReLU非线性。对于MC-dropout，我们在每个非线性之后添加dropout, dropout率为0.1结果如图2(a)所示。我们观察到，对抗训练和增加集合中网络的数量显著提高了分类精度以及NLL和Brier分数的性能，这表明我们的方法产生了校准良好的不确定性估计。对抗训练比随机方向的增强训练能带来更好的表现。我们的方法在所有性能指标上也比MC-dropout要好得多。请注意，用不变性(如随机裁剪和水平翻转)增强训练数据集是对抗性训练的补充，可以潜在地提高性能。

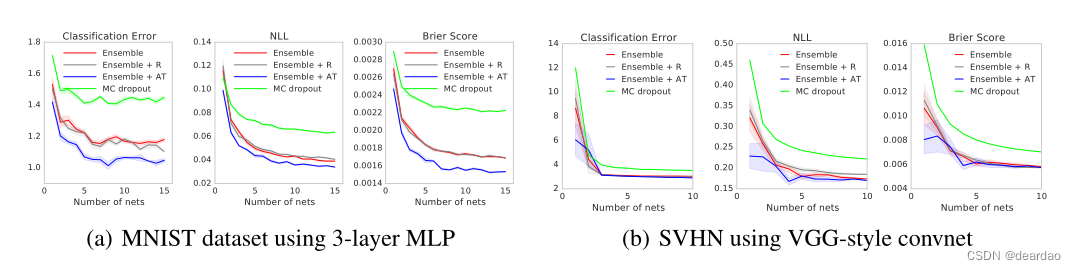
在这里插入图片描述

为了测量结果对网络结构选择的敏感性，我们实验了一个双层MLP和一个卷积神经网络;我们观察到定性相似的结果;看到详细内容见附录B.1中的补充材料。

不确定性评估:来自已知类和未知类的测试示例

在最后的实验中，我们评估了未见过的类的分布外示例的不确定性。对未知类的过度自信的预测对在现实世界应用中可靠地部署深度学习模型构成了挑战。当测试数据与训练数据非常不同时，我们希望预测显示出更高的不确定性。为了测试所提出的方法是否具有这种理想的特性，我们使用与以前相同的架构在标准MNIST训练/测试分割上训练MLP。然而，除了具有已知类的常规测试集之外，我们还在包含未知类的测试集上对其进行评估。我们使用NotMNIST10数据集的测试分割。该数据集中的图像与MNIST具有相同的大小，但是标签是字母而不是数字。我们无法获得真实的条件概率，但我们期望与已知类相比，未知类的预测更接近均匀，在已知类中，预测概率应该集中在真实目标上。我们评估预测分布的熵，并用它来评估不确定性估计的质量。结果如图3(a)所示。对于已知的类(上一行)，我们的方法和MC-dropout都具有预期的低熵。对于未知类(下一行)，随着M的增加，深度集成的熵增加得比MC-dropout快得多，这表明我们的方法更适合处理看不见的测试示例。特别是，MC-dropout似乎对一些测试例子给出了高置信度的预测，即使是看不见的职业，其模式也在0左右。在实践中，当在已知类和未知类的混合上进行测试时，这种过于自信的错误预测可能会产生问题，我们将在3.6节中看到。比较我们方法的不同变体，对抗训练模式的增长速度略快于香草集成模式，这表明对抗训练是有益的。
在这里插入图片描述