本文主要是介绍一种通过微电网形成的弹性配电系统模型,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
简介
使用分布式电源(DG)为形成多个微电网提供了一种弹性解决方案,以恢复配电系统中因自身故障损失的关键负荷。然而,随着微电网数量的增加,需要更多的虚拟二元和连续变量,因此将增加该模型的复杂性。为了解决这个问题,提出了一种新的模型来重新制定弹性配电网络中的微网的公式问题。与传统模型相比,二元变量和连续变量的数量都大大减少,计算性能显著提高。IEEE系统的数值结果验证了所提模型的有效性。
快速有效的恢复是提高配电系统弹性的关键步骤。随着分布式电源(DG)的渗透率不断提高,有意与 DG 分离被认为是通过在组件中断后提供关键负载来提高电力系统弹性的有效措施。具体而言,可通过启发式和穷举式搜索算法来寻找最佳孤岛。由于启发式或穷举式搜索方法可能无法保证全局最优解,因此可采用混合整数线性规划,其中提出了一种微电网形成方案,以在重大故障后拾取临界负荷,假设每个可控DG形成一个孤岛微电网。这项工作对使用DG的配电系统恢复具有重要意义,但其实施需要随着微电网数量的增加而增加决策变量,计算负担阻碍了其实用性。因此,本博文将为混合整数线性规划的模型提出一种新的数学公式,以减少决策变量的数量并提高计算性能。
弹性配电系统的微电网形成通过隔离开关进行分段形成不同的网络单元,其中每个微电网中只有一个 DG,以保证系统自给自足。目标是最大化自然灾害后拾取的荷载的总加权和,同时满足操作约束和拓扑约束。
约束条件
对于微电网,我们使用线性化的DistFlow潮流模型来制定微电网运行约束,从而给出约束条件(1)-(6)。具体来说,(1)意味着功率平衡;(2) 是 DistFlow 方潮流程。具体来说,如果支路闭合,则该支路的电压差受潮流约束,应限制支路流量;否则,电压差是任意的,支路流量必须为零;(3)给出每条母线的电压限制;(4)及(5)指输出限值;(6) 表示负荷需求上限。
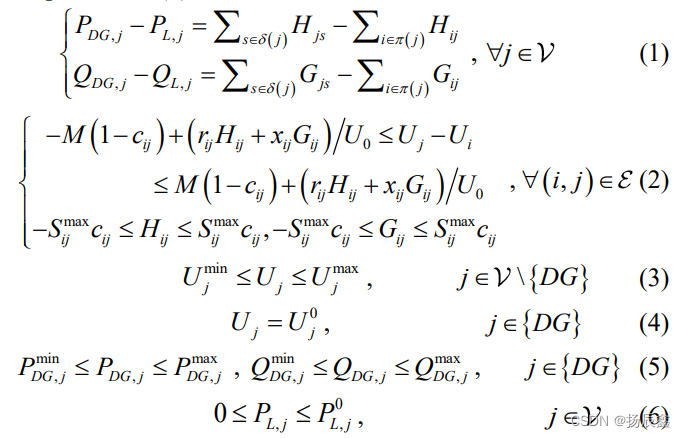
其中 Uj是母线 j 的电压大小;PDG,i和QDG,i为总线j处DG的有功和无功输出;PL,i 和 QL,i 为总线 j 处恢复的有功和无功负载需求;Hjs 和 Gjs 是从总线 j 到总线 s 的有功和无功功率;cij 表示分支 ij 的状态,如果 cij=1,则该分支关闭,否则该分支打开。Rij 和 xij 是支部 ij 的电阻和电抗;U0 j 是 DG 总线 j 处的指定电压值; 和 是一组公共汽车和分支;{DG} 是 DG 的集合;PDG,i min 和 PDG,i max 是总线 i 处 DG 的最小和最大有功功率限值;QDG,i min和QDG,i max为总线i处DG的最小和最大无功功率限值;Ui min 和 Ui max 是总线 i 的最小和最大电压限制;P 0 L,i为正常工况下的负荷需求;π(j) 和 δ(j) 是总线 j 的所有父母和子女的集合;Sij max 是分支 ij 的容量;M 是一个很大的数。
拓扑约束
考虑节点聚类约束、微电网连通约束和分支-节点约束来实现配电网划分为多个微电网。然而,与输电系统不同,配电系统具有拓扑结构呈径向的特性。因此,如果能够实现径向度,则将满足与拓扑相关的所有约束。由此来看,上述约束是多余的,可以简化为“径向约束”。一个充分且必要的径向条件,即当且仅当满足以下两个条件时,该图才是径向的:(i)每个子图都是一个连通图;(ii) 分支数等于节点数减去给定的子图数。
为了实现第一个条件,根据图论,可以使用单一商品流方法通过数学规划来制定子图连通性约束[6]。网络连接的条件基于单个物流的以下特征:设计一个具有相同拓扑结构的虚构网络,其中每个子图只有一个电源,称为“源”,所有其他总线(“源”总线除外)都有单位负载需求,充当“接收器”。由于虚构网络具有与原始电力网络相同的拓扑结构,因此它们具有相同的连接性。因此,虚构网络中每条总线的能量平衡满足意味着“源”总线和所有其他总线之间至少存在一条路径,因此必须连接子图。值得注意的是,可以在每个微电网中的任何总线上选择电源。在这项工作中,我们选择每个微电网中的DG总线作为“源”总线。因此可得到以下式子:
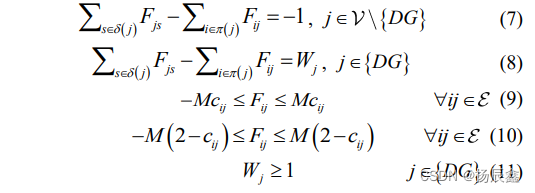
其中 |{●}|是集合 {●} 的基数;Fij 是虚构网络中线路 ij 上传输的功率;Wj 是虚构网络中由“源”总线提供的电源。
为了实现第二个条件:
![]()
值得注意的是,由于每个微电网仅包含一个分布式电源,因此微电网的数量与分布式电源相同。因此, |{DG}|是预先确定的参数。此外,设 wj 表示与总线 j 处的负载相关的优先级权重。最后,所提出的模型可以表述为 :
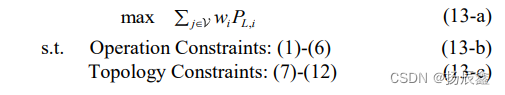
此模型与传统模型的比较 :
对比可以看出,连续变量(uj k,P k DG,j,Qk DG,j,δj k)定义为电压幅度、DG的有功和无功功率输出以及微电网 k的总线j处的松弛电压变量;二进制变量 vj k 表示总线 j 是否属于 微电网 k(如果总线 j 属于微电网 k,则 vj k=1,否则 vj k=0)。然后,分支节点约束显示 cij 和 vj k 之间的关系。然而,从表I中可以看出,[4]中的模型需要为每个微电网使用一组变量,因此变量的数量将随着微电网数量的增加而急剧增加。相比之下,无论微电网的数量如何,所提出的模型都不会增加太多。
表 1 变量数的比较
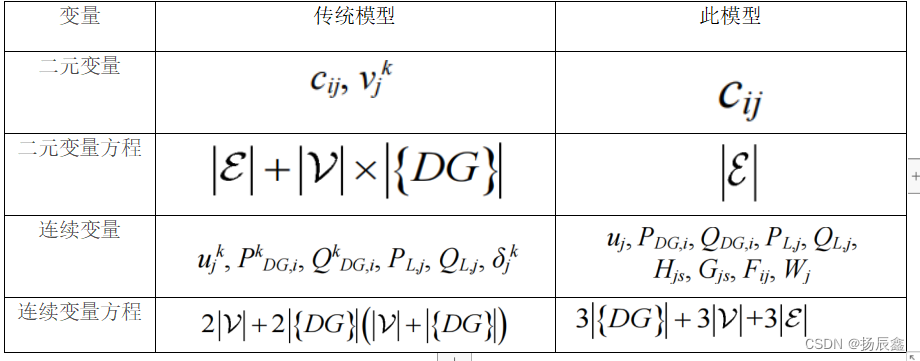
所提出的模型与传统中的模型的比较在一个大型615总线测试系统上进行了测试,该系统由五个123总线系统的组合组成。我们选择不同数量的 DG 进行说明,在事故发生后,整个配电系统与电网断开连接。此外,我们假设每个DG的最大有功和无功限制为500 kW和200 kVar,并且与负载相关的重量优先级权重相等。计算由GUROBI求解器计算机上进行。如表二所示,传统模型和所提出的模型实现了相同的最优目标值('obj.'),但随着微电网('NG')数量的增加,所提出的模型显著减少了二元变量('NB')和连续变量('NC')的数量。具体而言,NG=6时,NB和NC分别为传统模型和43%,NG=36时,NB和NC分别为传统模型中的3%和8%。这意味着随着 NG 的增加,更多的虚拟二进制和连续变量会减少。此外,对于计算时间('T.'),所提出的模型的运行速度比[传统模型的传统方法快15倍以上。特别是,随着NG的增加,将节省更多的计算时间。
这篇关于一种通过微电网形成的弹性配电系统模型的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








