本文主要是介绍记一次动态规划的采坑之旅, 741摘樱桃 https://leetcode.cn/problems/cherry-pickup/description/,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
首次看题目时,发现是困难。立马想到了,动态规划。
再看题目, 摘樱桃,还要返回摘两次,求摘最多的樱桃。
大脑第一反应就是:
先使用动态规划,找到 0 0 到 n-1 n-1处走过的最大樱桃, 并记录路径path。
然后根据路径path,将摘过的樱桃置为0,表示已经被摘过了。 然后再次摘樱桃。
两次摘过的樱桃之和就是目标的结果。
嗯,应该是,那就开写。
func cherryPickup(grid [][]int) int {ans := 0n := len(grid)dp := make([][]int, 0)for i := 0; i < n; i++ {dp = append(dp, make([]int, n))}// 1 表示上一个路径是 上// 2 表示上一个路径是 左path := make([][]int, 0)for i := 0; i < n; i++ {path = append(path, make([]int, n))}// 记录首次dp的轨迹,开始第一次摘for i := 0; i < len(grid); i++ {for j := 0; j < len(grid[0]); j++ {if i == 0 && j == 0 {dp[0][0] = grid[0][0]continue}if grid[i][j] == -1 {dp[i][j] = -1continue}if (i - 1 < 0 || grid[i-1][j] == -1 || dp[i-1][j] == -1) && (j - 1 < 0 || grid[i][j-1] == -1 || dp[i][j-1] == -1) {dp[i][j] = -1continue}if i - 1 < 0 || grid[i-1][j] == -1 || dp[i-1][j] == -1 {dp[i][j] = dp[i][j-1] + grid[i][j]path[i][j] = 2continue}if j - 1 < 0 || grid[i][j-1] == -1 || dp[i][j-1] == -1 {dp[i][j] = dp[i-1][j] + grid[i][j]path[i][j] = 1continue}if dp[i][j-1] > dp[i-1][j] {path[i][j] = 2dp[i][j] = dp[i][j-1] + grid[i][j]} else {path[i][j] = 1dp[i][j] = dp[i-1][j] + grid[i][j]}}}ans += dp[n-1][n-1]if ans == -1 {return 0}// 回溯路径, 清理已经被摘过的樱桃ii, jj := n-1, n-1for path[ii][jj] != 0 {grid[ii][jj] = 0if path[ii][jj] == 1 {ii--} else {jj--}}// 第二次摘樱桃grid[0][0] = 0dp = make([][]int, 0)for i := 0; i < n; i++ {dp = append(dp, make([]int, n))}for i := 0; i < len(grid); i++ {for j := 0; j < len(grid[0]); j++ {if i == 0 && j == 0 {dp[0][0] = grid[0][0]continue}if grid[i][j] == -1 {dp[i][j] = -1continue}if (i - 1 < 0 || grid[i-1][j] == -1 || dp[i-1][j] == -1) && (j - 1 < 0 || grid[i][j-1] == -1 || dp[i][j-1] == -1) {dp[i][j] = -1continue}if i - 1 < 0 || grid[i-1][j] == -1 || dp[i-1][j] == -1 {dp[i][j] = dp[i][j-1] + grid[i][j]path[i][j] = 2continue}if j - 1 < 0 || grid[i][j-1] == -1 || dp[i][j-1] == -1 {dp[i][j] = dp[i-1][j] + grid[i][j]path[i][j] = 1continue}if dp[i][j-1] > dp[i-1][j] {path[i][j] = 2dp[i][j] = dp[i][j-1] + grid[i][j]} else {path[i][j] = 1dp[i][j] = dp[i-1][j] + grid[i][j]}}}// 将两次摘的樱桃数相加return ans + dp[n-1][n-1]
}最后发现通过 53/59 , 差一点点点点。 其实差很多。
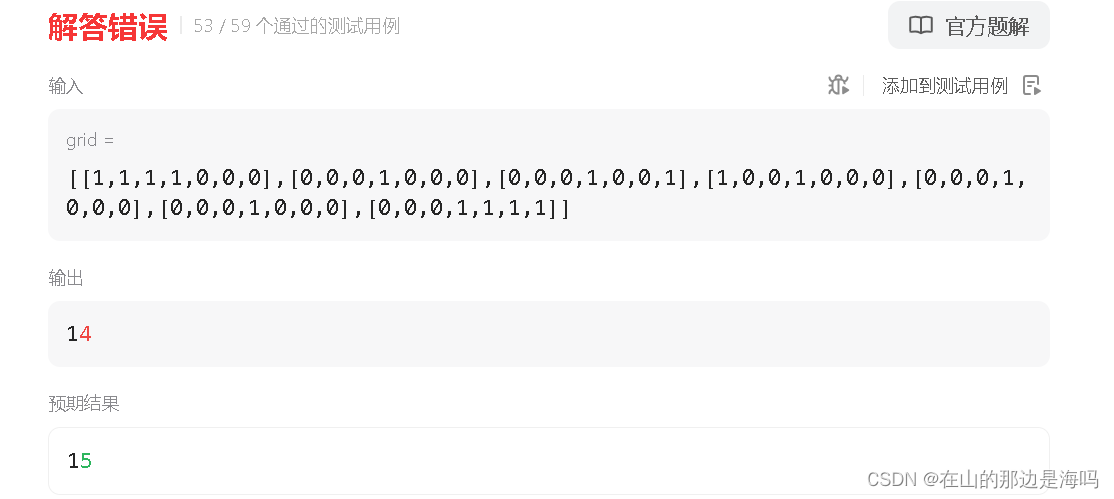
通过研究这个未通过的案例, 发现我虽然2次摘樱桃都是最大值, 但并不能证明最终采摘的樱桃数是最大的。
最后瞄了一眼答案, 来回摘2次樱桃数最多,又不能重复摘, 那找两个人同时摘不就好了吗。
附上leetcode标准答案
func cherryPickup(grid [][]int) int {n := len(grid)f := make([][][]int, n*2-1)for i := range f {f[i] = make([][]int, n)for j := range f[i] {f[i][j] = make([]int, n)for k := range f[i][j] {f[i][j][k] = math.MinInt32}}}f[0][0][0] = grid[0][0]for k := 1; k < n*2-1; k++ {for x1 := max(k-n+1, 0); x1 <= min(k, n-1); x1++ {y1 := k - x1if grid[x1][y1] == -1 {continue}for x2 := x1; x2 <= min(k, n-1); x2++ {y2 := k - x2if grid[x2][y2] == -1 {continue}res := f[k-1][x1][x2] // 都往右if x1 > 0 {res = max(res, f[k-1][x1-1][x2]) // 往下,往右}if x2 > 0 {res = max(res, f[k-1][x1][x2-1]) // 往右,往下}if x1 > 0 && x2 > 0 {res = max(res, f[k-1][x1-1][x2-1]) // 都往下}res += grid[x1][y1]if x2 != x1 { // 避免重复摘同一个樱桃res += grid[x2][y2]}f[k][x1][x2] = res}}}return max(f[n*2-2][n-1][n-1], 0)
}func min(a, b int) int {if a > b {return b}return a
}func max(a, b int) int {if b > a {return b}return a
}作者:力扣官方题解
链接:https://leetcode.cn/problems/cherry-pickup/solutions/1656418/zhai-ying-tao-by-leetcode-solution-1h3k/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。这篇关于记一次动态规划的采坑之旅, 741摘樱桃 https://leetcode.cn/problems/cherry-pickup/description/的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




