力扣hot100：543. 二叉树的直径/108. 将有序数组转换为二叉搜索树

本文主要是介绍力扣hot100：543. 二叉树的直径/108. 将有序数组转换为二叉搜索树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、543. 二叉树的直径

LeetCode：543. 二叉树的直径
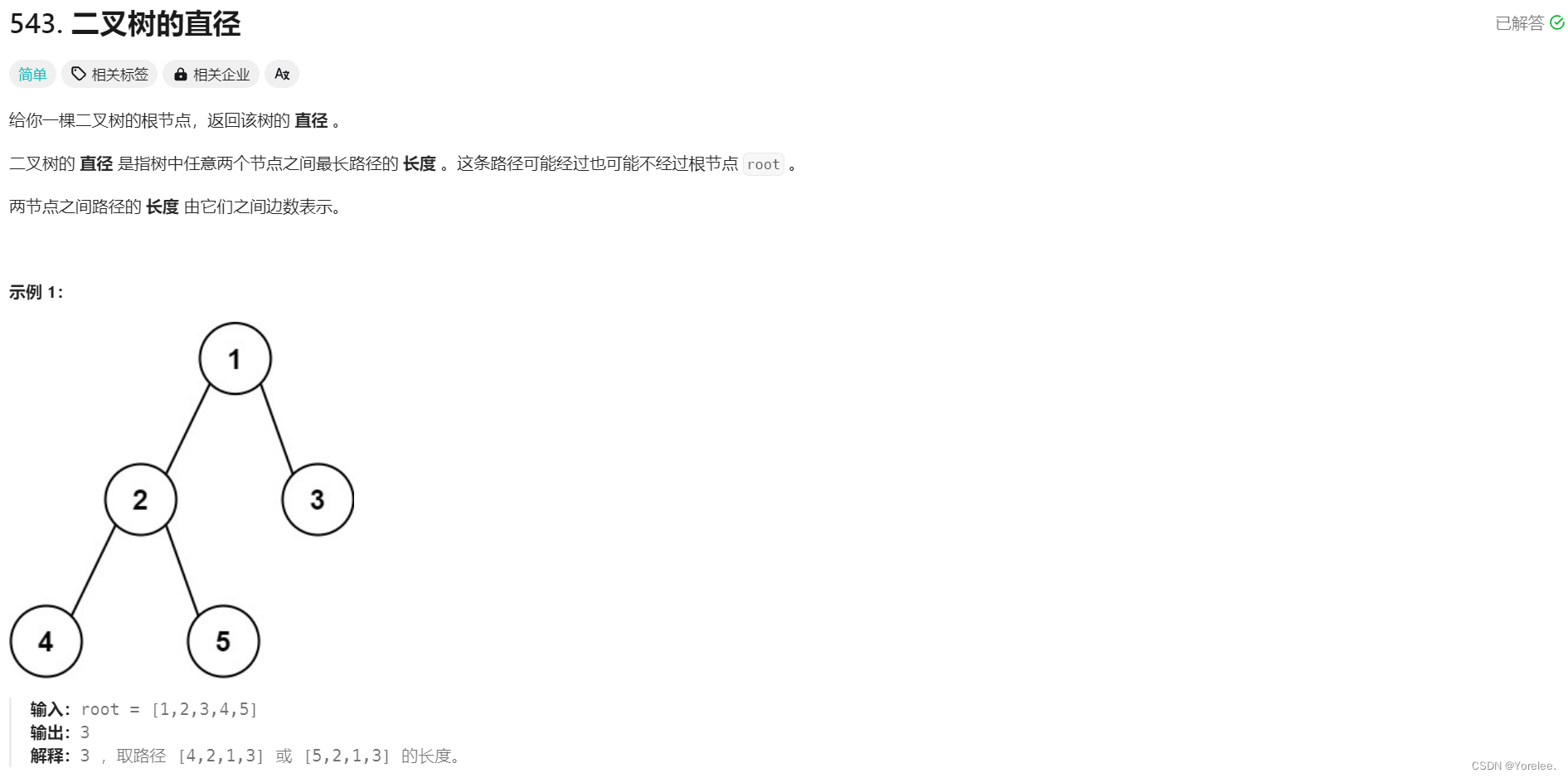
在这里插入图片描述

二叉树的直径 = 二叉树的直径是指树中任意两个节点之间最长路径的长度。

遇到二叉树的问题很容易去直接用求解的目标去定义递归函数。但是仔细考虑，返回树的直径并不能向上传播。因此我们可以拆分成两步：

树的直径 = 左儿子的高度 + 右儿子的高度 + 2

因此我们只需要求高度就行。

树求高度实际上是一个树形dp：dp[root] = max(dp[child]) +1

class Solution {
public:int diameterOfBinaryTree(TreeNode* root) {max_len = 0;height(root);return max_len;}
private:int height(TreeNode * root){if(!root) return -1;//没有结点时，高度为-1。有一个结点时，高度为0int left_height = height(root->left);//左儿子高度int right_height = height(root->right);//右儿子高度max_len = max(max_len, left_height + right_height + 2);return max(left_height, right_height) + 1;//返回以root为根的子树的高度。}int max_len;
};

二、108. 将有序数组转换为二叉搜索树

LeetCode：108. 将有序数组转换为二叉搜索树
在这里插入图片描述
二叉搜索树（二叉查找树）：对于任意节点，其左子树的所有节点的值小于该节点的值，其右子树的所有节点的值大于等于该节点的值。
这里需要注意的是，题目所给的nums 按严格递增顺序排列。因此，我们可以根据平衡二叉查找树的性质（左右子树高度差不大于1），通过下标直接找到根结点的位置（中间位置的结点）。

当总结点个数为奇数时，中间位置的结点左右两边的结点个数相同，很显然左右子树结点个数相同，采用相同形状则高度是相同的。
当总结点个数为偶数时，中间位置的结点右边的结点个数比左边结点个数多1。对于本中间位置结点而言，由于左右子树的生成规则相同，右子树的高度最多比左子树的高度多1。
程序递归执行，因此所有结点皆满足这样的性质，则可以构建一颗平衡二叉树。

类似于：构建完全二叉查找树

class Solution {
public:TreeNode* sortedArrayToBST(vector<int>& nums) {return createTree(nums, 0, nums.size()-1);}
private:TreeNode * createTree(vector<int> & nums, int L, int R){if(L > R) return nullptr;int mid = (L + R) >> 1;TreeNode * root = new TreeNode(nums[mid], createTree(nums, L, mid - 1), createTree(nums, mid + 1, R));return root;}
};