本文主要是介绍【三维重建】捆绑调整,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
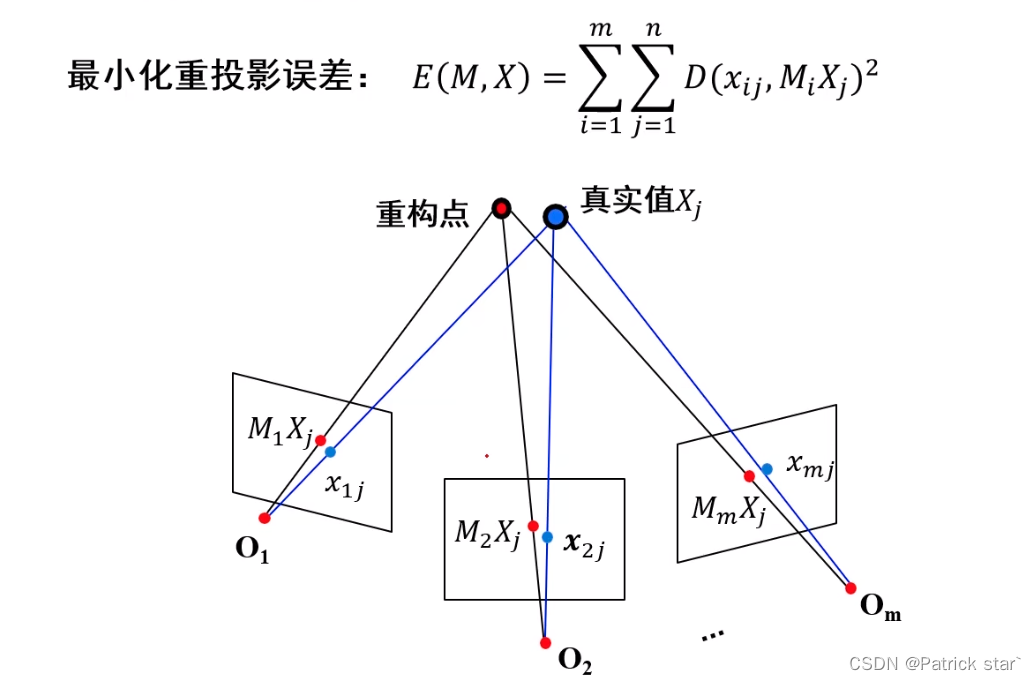
捆绑调整的目的是通过重构的点计算重投影误差,利用最优化方法是重投影误差最小。这是一个典型的非线性最小二乘问题,利用高斯-牛顿法进行优化(高斯-牛顿法原理参考https://blog.csdn.net/holle_world_ldx/article/details/138225785)
求雅可比矩阵
一、相机投影过程
1、世界坐标系到相机坐标系的变换
[ x c y c z c ] = R X + t = [ r 0 r 1 r 2 r 3 r 4 r 5 r 6 r 7 r 8 ] [ X Y Z ] + [ t 0 t 1 t 2 ] \begin{bmatrix} x_c\\ y_c\\ z_c \end{bmatrix}=RX+t=\begin{bmatrix}r_0 & r_1 &r_2 \\ r_3 & r_4 & r_5 \\ r_6 &r_7 &r_8 \end{bmatrix} \begin{bmatrix}X\\Y\\Z \end{bmatrix}+\begin{bmatrix}t_0\\t_1\\t_2\end{bmatrix} xcyczc =RX+t= r0r3r6r1r4r7r2r5r8 XYZ + t0t1t2
2、归一化像平面
x c = r 0 X + r 1 Y + r 2 Z + t 0 y c = r 3 X + r 4 Y + r 5 Z + t 1 z c = r 6 X + r 7 Y + r 8 Z + t 2 [ x y ] = [ x c z c y c z c ] \begin{aligned} &x_c = r_0X +r_1Y+r_2Z +t_0 \\ &y_c = r_3X +r_4Y+r_5Z +t_1 \\ &z_c = r_6X +r_7Y+r_8Z +t_2 \\ &\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix} \frac{x_c}{z_c}\\\frac{y_c}{z_c}\end{bmatrix} \end{aligned} xc=r0X+r1Y+r2Z+t0yc=r3X+r4Y+r5Z+t1zc=r6X+r7Y+r8Z+t2[xy]=[zcxczcyc]
3、相机成像平面
[ u v ] = [ f d ( k 0 , k 1 , r 2 ) x f d ( k 0 , k 1 , r 2 ) y ] , d ( k 0 , k 1 , r 2 ) = 1 + ( k 0 + k 1 r 2 ) r 2 , r 2 = x 2 + y 2 \begin{bmatrix}u\\v\end{bmatrix}=\begin{bmatrix} fd(k_0,k_1,r^2)x \\fd(k_0,k_1,r^2)y\end{bmatrix}, \ d(k_0,k_1,r^2)=1+(k_0+k_1r^2)r^2,\ r^2=x^2+y^2 [uv]=[fd(k0,k1,r2)xfd(k0,k1,r2)y], d(k0,k1,r2)=1+(k0+k1r2)r2, r2=x2+y2
二、Jacobian矩阵推导
1、计算焦距的偏导数 ∂ u ∂ f , ∂ v ∂ f \frac{\partial u}{\partial f},\frac{\partial v}{\partial f} ∂f∂u,∂f∂v
∂ u ∂ f = d ( k 0 , k 1 , r 2 ) x ∂ v ∂ f = d ( k 0 , k 1 , r 2 ) y \begin{aligned} \frac{\partial u}{\partial f}=d(k_0,k_1,r^2)x \\ \frac{\partial v}{\partial f}=d(k_0,k_1,r^2)y \end{aligned} ∂f∂u=d(k0,k1,r2)x∂f∂v=d(k0,k1,r2)y
2、计算径向畸变系数 ∂ u ∂ k 0 , ∂ u ∂ k 1 , ∂ v ∂ k 0 , ∂ v ∂ k 1 \frac{\partial u}{\partial k_0},\frac{\partial u}{\partial k_1},\frac{\partial v}{\partial k_0},\frac{\partial v}{\partial k_1} ∂k0∂u,∂k1∂u,∂k0∂v,∂k1∂v
引入中间变量:
∂ u ∂ d ( k 0 , k 1 , r 2 ) = f x ∂ v ∂ d ( k 0 , k 1 , r 2 ) = f y ∂ d ( k 0 , k 1 , r 2 ) ∂ d ( k 0 ) = r 2 ∂ d ( k 0 , k 1 , r 2 ) ∂ d ( k 1 ) = r 4 \begin{aligned} \frac{\partial u}{\partial d(k_0,k_1,r^2)} = fx \\ \frac{\partial v}{\partial d(k_0,k_1,r^2)} = fy \\ \frac{\partial d(k_0,k_1,r^2)}{\partial d(k_0)} = r^2 \\ \frac{\partial d(k_0,k_1,r^2)}{\partial d(k_1)} = r^4 \end{aligned} ∂d(k0,k1,r2)∂u=fx∂d(k0,k1,r2)∂v=fy∂d(k0)∂d(k0,k1,r2)=r2∂d(k1)∂d(k0,k1,r2)=r4
根据链式法则:
∂ u ∂ k 0 = ∂ u ∂ d ( k 0 , k 1 , r 2 ) ∂ d ( k 0 , k 1 , r 2 ) k 0 = f x r 2 ∂ u ∂ k 1 = ∂ u ∂ d ( k 0 , k 1 , r 2 ) ∂ d ( k 0 , k 1 , r 2 ) k 1 = f x r 4 ∂ v ∂ k 0 = ∂ v ∂ d ( k 0 , k 1 , r 2 ) ∂ d ( k 0 , k 1 , r 2 ) k 0 = f y r 2 ∂ v ∂ k 1 = ∂ v ∂ d ( k 0 , k 1 , r 2 ) ∂ d ( k 0 , k 1 , r 2 ) k 1 = f y r 4 \begin{aligned} \frac{\partial u}{\partial k_0} = \frac{\partial u}{\partial d(k_0,k_1,r^2)} \frac{\partial d(k_0,k_1,r^2)}{k_0}=fxr^2 \\ \frac{\partial u}{\partial k_1} = \frac{\partial u}{\partial d(k_0,k_1,r^2)} \frac{\partial d(k_0,k_1,r^2)}{k_1}=fxr^4 \\ \frac{\partial v}{\partial k_0} = \frac{\partial v}{\partial d(k_0,k_1,r^2)} \frac{\partial d(k_0,k_1,r^2)}{k_0}=fyr^2 \\ \frac{\partial v}{\partial k_1} = \frac{\partial v}{\partial d(k_0,k_1,r^2)} \frac{\partial d(k_0,k_1,r^2)}{k_1}=fyr^4 \\ \end{aligned} ∂k0∂u=∂d(k0,k1,r2)∂uk0∂d(k0,k1,r2)=fxr2∂k1∂u=∂d(k0,k1,r2)∂uk1∂d(k0,k1,r2)=fxr4∂k0∂v=∂d(k0,k1,r2)∂vk0∂d(k0,k1,r2)=fyr2∂k1∂v=∂d(k0,k1,r2)∂vk1∂d(k0,k1,r2)=fyr4
3、计算关于平移向量的偏导 ∂ u ∂ t 0 , ∂ u ∂ t 1 , ∂ u ∂ t 2 , ∂ v ∂ t 0 , ∂ v ∂ t 1 , ∂ v ∂ t 2 \frac{\partial u}{\partial t_0},\frac{\partial u}{\partial t_1},\frac{\partial u}{\partial t_2},\frac{\partial v}{\partial t_0},\frac{\partial v}{\partial t_1},\frac{\partial v}{\partial t_2} ∂t0∂u,∂t1∂u,∂t2∂u,∂t0∂v,∂t1∂v,∂t2∂v
∂ x c ∂ t 0 = 1 , ∂ y c ∂ t 1 = 1 , ∂ z c ∂ t 2 = 1 ∂ x ∂ x c = 1 z c , ∂ y ∂ y c = 1 z c , ∂ x ∂ z c = − x c ( z c ) 2 , ∂ y ∂ z c = − y c ( z c ) 2 ∂ x ∂ t 0 = ∂ x ∂ x c ∂ x c ∂ t 0 , ∂ y ∂ t 1 = ∂ y ∂ y c ∂ y c ∂ t 1 , ∂ x ∂ t 2 = ∂ x ∂ z c ∂ z c ∂ t 2 , ∂ y ∂ t 2 = ∂ y ∂ z c ∂ z c ∂ t 2 ∂ r 2 ∂ x = 2 x , ∂ r 2 ∂ y = 2 y , ∂ r 2 ∂ t 0 = ∂ r 2 ∂ x ∂ x ∂ t 0 , ∂ r 2 ∂ t 1 = ∂ r 2 ∂ y ∂ y ∂ t 1 , ∂ r 2 ∂ t 2 = ∂ r 2 ∂ x ∂ x ∂ t 2 + ∂ r 2 ∂ y ∂ y ∂ t 2 ∂ d ∂ r 2 = k 0 + 2 k 1 r 2 , ∂ d ∂ t 0 = ∂ d ∂ r 2 ∂ r 2 ∂ t 0 , ∂ d ∂ t 1 = ∂ d ∂ r 2 ∂ r 2 ∂ t 1 , ∂ d ∂ t 2 = ∂ d ∂ r 2 ∂ r 2 ∂ t 2 ∂ d ∂ x = ∂ d ∂ r 2 ∂ r 2 ∂ x , ∂ u ∂ x = f d + f x ∂ d ∂ x , ∂ d ∂ y = ∂ d ∂ r 2 ∂ r 2 ∂ y , ∂ v ∂ y = f d + f y ∂ d ∂ y ∂ u ∂ t 0 = ∂ u ∂ d ∂ d ∂ t 0 x + ∂ u ∂ x ∂ x ∂ t 0 d , ∂ u ∂ t 1 = ∂ u ∂ d ∂ d ∂ t 1 x , ∂ u ∂ t 2 = ∂ u ∂ d ∂ d ∂ t 2 x + ∂ u ∂ x ∂ x ∂ t 2 d ∂ v ∂ t 0 = ∂ v ∂ d ∂ d ∂ t 0 y , ∂ v ∂ t 1 = ∂ v ∂ d ∂ d ∂ t 1 y + ∂ v ∂ y ∂ y ∂ t 1 d , ∂ v ∂ t 2 = ∂ v ∂ d ∂ d ∂ t 2 y + ∂ v ∂ y ∂ y ∂ t 2 d \begin{aligned} &\frac{\partial x_c}{\partial t_0}=1 ,{\kern 10pt} \frac{\partial y_c}{\partial t_1}=1 ,{\kern 10pt} \frac{\partial z_c}{\partial t_2}=1 \\ &\frac{\partial x}{\partial x_c}=\frac{1}{z_c} ,{\kern 10pt} \frac{\partial y}{\partial y_c}=\frac{1}{z_c} ,{\kern 10pt}\frac{\partial x}{\partial z_c}=-\frac{x_c}{(z_c)^2},{\kern 10pt} \frac{\partial y}{\partial z_c}=-\frac{y_c}{(z_c)^2} \\ &\frac{\partial x}{\partial t_0} = \frac{\partial x}{\partial x_c}\frac{\partial x_c}{\partial t_0},{\kern 10pt}\frac{\partial y}{\partial t_1} = \frac{\partial y}{\partial y_c}\frac{\partial y_c}{\partial t_1},{\kern 10pt}\frac{\partial x}{\partial t_2} = \frac{\partial x}{\partial z_c}\frac{\partial z_c}{\partial t_2},{\kern 10pt} \frac{\partial y}{\partial t_2} = \frac{\partial y}{\partial z_c}\frac{\partial z_c}{\partial t_2} \\ &\frac{\partial r^2}{\partial x} = 2x,{\kern 10pt}\frac{\partial r^2}{\partial y} = 2y,{\kern 10pt} \frac{\partial r^2}{\partial t_0} = \frac{\partial r^2}{\partial x}\frac{\partial x}{\partial t_0},{\kern 10pt}\frac{\partial r^2}{\partial t_1} = \frac{\partial r^2}{\partial y}\frac{\partial y}{\partial t_1},{\kern 10pt}\frac{\partial r^2}{\partial t_2} = \frac{\partial r^2}{\partial x}\frac{\partial x}{\partial t_2} + \frac{\partial r^2}{\partial y}\frac{\partial y}{\partial t_2}\\ &\frac{\partial d}{\partial r^2}=k_0 + 2 k_1r^2,{\kern 10pt}\frac{\partial d}{\partial t_0} = \frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial t_0} ,{\kern 10pt}\frac{\partial d}{\partial t_1} = \frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial t_1} ,{\kern 10pt}\frac{\partial d}{\partial t_2} = \frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial t_2}\\ &\frac{\partial d}{\partial x}=\frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial x} ,{\kern 10pt}\frac{\partial u}{\partial x} = fd+fx\frac{\partial d}{\partial x} ,{\kern 10pt}\frac{\partial d}{\partial y}=\frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial y} ,{\kern 10pt}\frac{\partial v}{\partial y} = fd+fy\frac{\partial d}{\partial y} \\ &\color{red} \frac{\partial u}{\partial t_0} = \frac{\partial u}{\partial d}\frac{\partial d}{\partial t_0}x +\frac{\partial u}{\partial x}\frac{\partial x}{\partial t_0}d ,{\kern 10pt}\frac{\partial u}{\partial t_1} = \frac{\partial u}{\partial d}\frac{\partial d}{\partial t_1}x,{\kern 10pt}\frac{\partial u}{\partial t_2} = \frac{\partial u}{\partial d}\frac{\partial d}{\partial t_2}x +\frac{\partial u}{\partial x}\frac{\partial x}{\partial t_2}d \color{black}\\ &\color{red} \frac{\partial v}{\partial t_0} = \frac{\partial v}{\partial d}\frac{\partial d}{\partial t_0}y ,{\kern 10pt}\frac{\partial v}{\partial t_1} = \frac{\partial v}{\partial d}\frac{\partial d}{\partial t_1}y+\frac{\partial v}{\partial y}\frac{\partial y}{\partial t_1}d,{\kern 10pt}\frac{\partial v}{\partial t_2} = \frac{\partial v}{\partial d}\frac{\partial d}{\partial t_2}y +\frac{\partial v}{\partial y}\frac{\partial y}{\partial t_2}d \color{black} \end{aligned} ∂t0∂xc=1,∂t1∂yc=1,∂t2∂zc=1∂xc∂x=zc1,∂yc∂y=zc1,∂zc∂x=−(zc)2xc,∂zc∂y=−(zc)2yc∂t0∂x=∂xc∂x∂t0∂xc,∂t1∂y=∂yc∂y∂t1∂yc,∂t2∂x=∂zc∂x∂t2∂zc,∂t2∂y=∂zc∂y∂t2∂zc∂x∂r2=2x,∂y∂r2=2y,∂t0∂r2=∂x∂r2∂t0∂x,∂t1∂r2=∂y∂r2∂t1∂y,∂t2∂r2=∂x∂r2∂t2∂x+∂y∂r2∂t2∂y∂r2∂d=k0+2k1r2,∂t0∂d=∂r2∂d∂t0∂r2,∂t1∂d=∂r2∂d∂t1∂r2,∂t2∂d=∂r2∂d∂t2∂r2∂x∂d=∂r2∂d∂x∂r2,∂x∂u=fd+fx∂x∂d,∂y∂d=∂r2∂d∂y∂r2,∂y∂v=fd+fy∂y∂d∂t0∂u=∂d∂u∂t0∂dx+∂x∂u∂t0∂xd,∂t1∂u=∂d∂u∂t1∂dx,∂t2∂u=∂d∂u∂t2∂dx+∂x∂u∂t2∂xd∂t0∂v=∂d∂v∂t0∂dy,∂t1∂v=∂d∂v∂t1∂dy+∂y∂v∂t1∂yd,∂t2∂v=∂d∂v∂t2∂dy+∂y∂v∂t2∂yd
4、计算关于旋转向量的偏导 ∂ u ∂ r 0 , ∂ u ∂ r 2 , ∂ u ∂ r 3 , ∂ u ∂ r 4 , ∂ u ∂ r 5 , ∂ u ∂ r 6 , ∂ u ∂ r 7 , ∂ u ∂ r 8 \frac{\partial u}{\partial r_0},\frac{\partial u}{\partial r_2},\frac{\partial u}{\partial r_3},\frac{\partial u}{\partial r_4},\frac{\partial u}{\partial r_5},\frac{\partial u}{\partial r_6},\frac{\partial u}{\partial r_7},\frac{\partial u}{\partial r_8} ∂r0∂u,∂r2∂u,∂r3∂u,∂r4∂u,∂r5∂u,∂r6∂u,∂r7∂u,∂r8∂u ∂ v ∂ r 0 , ∂ v ∂ r 2 , ∂ v ∂ r 3 , ∂ v ∂ r 4 , ∂ v ∂ r 5 , ∂ v ∂ r 6 , ∂ v ∂ r 7 , ∂ v ∂ r 8 \frac{\partial v}{\partial r_0},\frac{\partial v}{\partial r_2},\frac{\partial v}{\partial r_3},\frac{\partial v}{\partial r_4},\frac{\partial v}{\partial r_5},\frac{\partial v}{\partial r_6},\frac{\partial v}{\partial r_7},\frac{\partial v}{\partial r_8} ∂r0∂v,∂r2∂v,∂r3∂v,∂r4∂v,∂r5∂v,∂r6∂v,∂r7∂v,∂r8∂v
∂ x c ∂ r 0 = ∂ y c ∂ r 3 = ∂ z c ∂ r 6 = X , ∂ x c ∂ r 1 = ∂ y c ∂ r 4 = ∂ z c ∂ r 7 = Y , ∂ x c ∂ r 2 = ∂ y c ∂ r 5 = ∂ z c ∂ r 8 = Z ∂ r 2 ∂ r 0 = ∂ r 2 ∂ x ∂ x ∂ x c ∂ x c ∂ r 0 , ∂ r 2 ∂ r 1 = ∂ r 2 ∂ x ∂ x ∂ x c ∂ x c ∂ r 1 , ∂ r 2 ∂ r 2 = ∂ r 2 ∂ x ∂ x ∂ x c ∂ x c ∂ r 2 ∂ r 2 ∂ r 3 = ∂ r 2 ∂ y ∂ y ∂ y c ∂ y c ∂ r 3 , ∂ r 2 ∂ r 4 = ∂ r 2 ∂ y ∂ y ∂ y c ∂ y c ∂ r 4 , ∂ r 2 ∂ r 5 = ∂ r 2 ∂ y ∂ y ∂ y c ∂ y c ∂ r 5 ∂ r 2 ∂ r 6 = ∂ r 2 ∂ x ∂ x ∂ z c ∂ z c ∂ r 6 + ∂ r 2 ∂ y ∂ y ∂ z c ∂ z c ∂ r 6 , ∂ r 2 ∂ r 7 = ∂ r 2 ∂ x ∂ x ∂ z c ∂ z c ∂ r 7 + ∂ r 2 ∂ y ∂ y ∂ z c ∂ z c ∂ r 7 , ∂ r 2 ∂ r 8 = ∂ r 2 ∂ x ∂ x ∂ z c ∂ z c ∂ r 8 + ∂ r 2 ∂ y ∂ y ∂ z c ∂ z c ∂ r 8 ∂ d ∂ r 0 = ∂ d ∂ r 2 ∂ r 2 ∂ r 0 , ∂ d ∂ r 1 = ∂ d ∂ r 2 ∂ r 2 ∂ r 1 , ∂ d ∂ r 2 = ∂ d ∂ r 2 ∂ r 2 ∂ r 2 ∂ d ∂ r 3 = ∂ d ∂ r 2 ∂ r 2 ∂ r 3 , ∂ d ∂ r 4 = ∂ d ∂ r 2 ∂ r 2 ∂ r 4 , ∂ d ∂ r 5 = ∂ d ∂ r 2 ∂ r 2 ∂ r 5 ∂ d ∂ r 6 = ∂ d ∂ r 2 ∂ r 2 ∂ r 6 , ∂ d ∂ r 7 = ∂ d ∂ r 2 ∂ r 2 ∂ r 7 , ∂ d ∂ r 8 = ∂ d ∂ r 2 ∂ r 2 ∂ r 8 ∂ x ∂ r 0 = ∂ x ∂ x c ∂ x c ∂ r 0 , ∂ x ∂ r 1 = ∂ x ∂ x c ∂ x c ∂ r 1 , ∂ x ∂ r 2 = ∂ x ∂ x c ∂ x c ∂ r 2 , ∂ x ∂ r 6 = ∂ x ∂ z c ∂ z c ∂ r 6 , ∂ x ∂ r 7 = ∂ x ∂ z c ∂ z c ∂ r 7 , ∂ x ∂ r 8 = ∂ x ∂ z c ∂ z c ∂ r 8 ∂ u ∂ r 0 = f x ∂ d ∂ r 0 + f d ∂ x ∂ r 0 , ∂ u ∂ r 1 = f x ∂ d ∂ r 1 + f d ∂ x ∂ r 1 , ∂ u ∂ r 2 = f x ∂ d ∂ r 2 + f d ∂ x ∂ r 2 ∂ u ∂ r 3 = f x ∂ d ∂ r 3 , ∂ u ∂ r 4 = f x ∂ d ∂ r 4 , ∂ u ∂ r 5 = f x ∂ d ∂ r 5 ∂ u ∂ r 6 = f x ∂ d ∂ r 6 + f d ∂ x ∂ r 6 , ∂ u ∂ r 7 = f x ∂ d ∂ r 7 + f d ∂ x ∂ r 7 , ∂ u ∂ r 8 = f x ∂ d ∂ r 8 + f d ∂ x ∂ r 8 ∂ y ∂ r 3 = ∂ y ∂ y c ∂ y c ∂ r 3 , ∂ y ∂ r 4 = ∂ y ∂ y c ∂ y c ∂ r 4 , ∂ y ∂ r 5 = ∂ y ∂ y c ∂ y c ∂ r 5 , ∂ y ∂ r 6 = ∂ y ∂ z c ∂ z c ∂ r 6 , ∂ y ∂ r 7 = ∂ y ∂ z c ∂ z c ∂ r 7 , ∂ y ∂ r 8 = ∂ y ∂ z c ∂ z c ∂ r 8 ∂ v ∂ r 0 = f y ∂ d ∂ r 0 , ∂ v ∂ r 1 = f y ∂ d ∂ r 1 , ∂ v ∂ r 2 = f y ∂ d ∂ r 2 ∂ v ∂ r 3 = f y ∂ d ∂ r 3 + f d ∂ y ∂ r 3 , ∂ v ∂ r 4 = f y ∂ d ∂ r 4 + f d ∂ y ∂ r 4 , ∂ v ∂ r 5 = f u ∂ d ∂ r 5 + f d ∂ y ∂ r 5 ∂ v ∂ r 6 = f y ∂ d ∂ r 6 + f d ∂ y ∂ r 6 , ∂ v ∂ r 7 = f y ∂ d ∂ r 7 + f d ∂ y ∂ r 7 , ∂ v ∂ r 8 = f y ∂ d ∂ r 8 + f d ∂ y ∂ r 8 \begin{aligned} &\frac{\partial x_c}{\partial r_0} =\frac{\partial y_c}{\partial r_3} =\frac{\partial z_c}{\partial r_6} = X ,{\kern 10pt}\frac{\partial x_c}{\partial r_1} =\frac{\partial y_c}{\partial r_4} =\frac{\partial z_c}{\partial r_7} = Y ,{\kern 10pt}\frac{\partial x_c}{\partial r_2} =\frac{\partial y_c}{\partial r_5} = \frac{\partial z_c}{\partial r_8} = Z \\\\ &\frac{\partial r^2}{\partial r_0}=\frac{\partial r^2}{\partial x}\frac{\partial x}{\partial x_c}\frac{\partial x_c}{\partial r_0},{\kern 10pt}\frac{\partial r^2}{\partial r_1}=\frac{\partial r^2}{\partial x}\frac{\partial x}{\partial x_c}\frac{\partial x_c}{\partial r_1},{\kern 10pt}\frac{\partial r^2}{\partial r_2}=\frac{\partial r^2}{\partial x}\frac{\partial x}{\partial x_c}\frac{\partial x_c}{\partial r_2}\\ & \frac{\partial r^2}{\partial r_3}=\frac{\partial r^2}{\partial y}\frac{\partial y}{\partial y_c}\frac{\partial y_c}{\partial r_3},{\kern 10pt}\frac{\partial r^2}{\partial r_4}=\frac{\partial r^2}{\partial y}\frac{\partial y}{\partial y_c}\frac{\partial y_c}{\partial r_4} ,{\kern 10pt}\frac{\partial r^2}{\partial r_5}=\frac{\partial r^2}{\partial y}\frac{\partial y}{\partial y_c}\frac{\partial y_c}{\partial r_5} \\ & \frac{\partial r^2}{\partial r_6}=\frac{\partial r^2}{\partial x}\frac{\partial x}{\partial z_c}\frac{\partial z_c}{\partial r_6}+\frac{\partial r^2}{\partial y}\frac{\partial y}{\partial z_c}\frac{\partial z_c}{\partial r_6},{\kern 10pt}\frac{\partial r^2}{\partial r_7}=\frac{\partial r^2}{\partial x}\frac{\partial x}{\partial z_c}\frac{\partial z_c}{\partial r_7}+\frac{\partial r^2}{\partial y}\frac{\partial y}{\partial z_c}\frac{\partial z_c}{\partial r_7},{\kern 10pt}\frac{\partial r^2}{\partial r_8}=\frac{\partial r^2}{\partial x}\frac{\partial x}{\partial z_c}\frac{\partial z_c}{\partial r_8}+\frac{\partial r^2}{\partial y}\frac{\partial y}{\partial z_c}\frac{\partial z_c}{\partial r_8}\\\\ &\frac{\partial d}{\partial r_0}=\frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial r_0},{\kern 10pt}\frac{\partial d}{\partial r_1}=\frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial r_1},{\kern 10pt}\frac{\partial d}{\partial r_2}=\frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial r_2}\\ &\frac{\partial d}{\partial r_3}=\frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial r_3},{\kern 10pt}\frac{\partial d}{\partial r_4}=\frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial r_4},{\kern 10pt}\frac{\partial d}{\partial r_5}=\frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial r_5} \\ &\frac{\partial d}{\partial r_6}=\frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial r_6},{\kern 10pt}\frac{\partial d}{\partial r_7}=\frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial r_7},{\kern 10pt}\frac{\partial d}{\partial r_8}=\frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial r_8} \\\\ &\frac{\partial x}{\partial r_0}=\frac{\partial x}{\partial x_c}\frac{\partial x_c}{\partial r_0},{\kern 10pt}\frac{\partial x}{\partial r_1}=\frac{\partial x}{\partial x_c}\frac{\partial x_c}{\partial r_1},{\kern 10pt}\frac{\partial x}{\partial r_2}=\frac{\partial x}{\partial x_c}\frac{\partial x_c}{\partial r_2},{\kern 10pt} \frac{\partial x}{\partial r_6}=\frac{\partial x}{\partial z_c}\frac{\partial z_c}{\partial r_6},{\kern 10pt}\frac{\partial x}{\partial r_7}=\frac{\partial x}{\partial z_c}\frac{\partial z_c}{\partial r_7},{\kern 10pt}\frac{\partial x}{\partial r_8}=\frac{\partial x}{\partial z_c}\frac{\partial z_c}{\partial r_8} \\\\ &\color{red}\frac{\partial u}{\partial r_0} = fx\frac{\partial d}{\partial r_0}+fd\frac{\partial x}{\partial r_0},{\kern 10pt}\frac{\partial u}{\partial r_1} = fx\frac{\partial d}{\partial r_1}+fd\frac{\partial x}{\partial r_1},{\kern 10pt}\frac{\partial u}{\partial r_2} = fx\frac{\partial d}{\partial r_2}+fd\frac{\partial x}{\partial r_2}\\ &\color{red}\frac{\partial u}{\partial r_3} = fx\frac{\partial d}{\partial r_3},{\kern 10pt}\frac{\partial u}{\partial r_4} = fx\frac{\partial d}{\partial r_4},{\kern 10pt}\frac{\partial u}{\partial r_5} = fx\frac{\partial d}{\partial r_5}\\ &\color{red}\frac{\partial u}{\partial r_6} = fx\frac{\partial d}{\partial r_6}+fd\frac{\partial x}{\partial r_6},{\kern 10pt}\frac{\partial u}{\partial r_7} = fx\frac{\partial d}{\partial r_7}+fd\frac{\partial x}{\partial r_7},{\kern 10pt}\frac{\partial u}{\partial r_8} = fx\frac{\partial d}{\partial r_8}+fd\frac{\partial x}{\partial r_8}\\\\ &\frac{\partial y}{\partial r_3}=\frac{\partial y}{\partial y_c}\frac{\partial y_c}{\partial r_3},{\kern 10pt}\frac{\partial y}{\partial r_4}=\frac{\partial y}{\partial y_c}\frac{\partial y_c}{\partial r_4},{\kern 10pt}\frac{\partial y}{\partial r_5}=\frac{\partial y}{\partial y_c}\frac{\partial y_c}{\partial r_5},{\kern 10pt} \frac{\partial y}{\partial r_6}=\frac{\partial y}{\partial z_c}\frac{\partial z_c}{\partial r_6},{\kern 10pt}\frac{\partial y}{\partial r_7}=\frac{\partial y}{\partial z_c}\frac{\partial z_c}{\partial r_7},{\kern 10pt}\frac{\partial y}{\partial r_8}=\frac{\partial y}{\partial z_c}\frac{\partial z_c}{\partial r_8} \\\\ &\color{red}\frac{\partial v}{\partial r_0} = fy\frac{\partial d}{\partial r_0},{\kern 10pt}\frac{\partial v}{\partial r_1} = fy\frac{\partial d}{\partial r_1},{\kern 10pt}\frac{\partial v}{\partial r_2} = fy\frac{\partial d}{\partial r_2}\\ &\color{red}\frac{\partial v}{\partial r_3} = fy\frac{\partial d}{\partial r_3}+fd\frac{\partial y}{\partial r_3},{\kern 10pt}\frac{\partial v}{\partial r_4} = fy\frac{\partial d}{\partial r_4}+fd\frac{\partial y}{\partial r_4},{\kern 10pt}\frac{\partial v}{\partial r_5} = fu\frac{\partial d}{\partial r_5}+fd\frac{\partial y}{\partial r_5}\\ &\color{red}\frac{\partial v}{\partial r_6} = fy\frac{\partial d}{\partial r_6}+fd\frac{\partial y}{\partial r_6},{\kern 10pt}\frac{\partial v}{\partial r_7} = fy\frac{\partial d}{\partial r_7}+fd\frac{\partial y}{\partial r_7},{\kern 10pt}\frac{\partial v}{\partial r_8} = fy\frac{\partial d}{\partial r_8}+fd\frac{\partial y}{\partial r_8}\\ \end{aligned} ∂r0∂xc=∂r3∂yc=∂r6∂zc=X,∂r1∂xc=∂r4∂yc=∂r7∂zc=Y,∂r2∂xc=∂r5∂yc=∂r8∂zc=Z∂r0∂r2=∂x∂r2∂xc∂x∂r0∂xc,∂r1∂r2=∂x∂r2∂xc∂x∂r1∂xc,∂r2∂r2=∂x∂r2∂xc∂x∂r2∂xc∂r3∂r2=∂y∂r2∂yc∂y∂r3∂yc,∂r4∂r2=∂y∂r2∂yc∂y∂r4∂yc,∂r5∂r2=∂y∂r2∂yc∂y∂r5∂yc∂r6∂r2=∂x∂r2∂zc∂x∂r6∂zc+∂y∂r2∂zc∂y∂r6∂zc,∂r7∂r2=∂x∂r2∂zc∂x∂r7∂zc+∂y∂r2∂zc∂y∂r7∂zc,∂r8∂r2=∂x∂r2∂zc∂x∂r8∂zc+∂y∂r2∂zc∂y∂r8∂zc∂r0∂d=∂r2∂d∂r0∂r2,∂r1∂d=∂r2∂d∂r1∂r2,∂r2∂d=∂r2∂d∂r2∂r2∂r3∂d=∂r2∂d∂r3∂r2,∂r4∂d=∂r2∂d∂r4∂r2,∂r5∂d=∂r2∂d∂r5∂r2∂r6∂d=∂r2∂d∂r6∂r2,∂r7∂d=∂r2∂d∂r7∂r2,∂r8∂d=∂r2∂d∂r8∂r2∂r0∂x=∂xc∂x∂r0∂xc,∂r1∂x=∂xc∂x∂r1∂xc,∂r2∂x=∂xc∂x∂r2∂xc,∂r6∂x=∂zc∂x∂r6∂zc,∂r7∂x=∂zc∂x∂r7∂zc,∂r8∂x=∂zc∂x∂r8∂zc∂r0∂u=fx∂r0∂d+fd∂r0∂x,∂r1∂u=fx∂r1∂d+fd∂r1∂x,∂r2∂u=fx∂r2∂d+fd∂r2∂x∂r3∂u=fx∂r3∂d,∂r4∂u=fx∂r4∂d,∂r5∂u=fx∂r5∂d∂r6∂u=fx∂r6∂d+fd∂r6∂x,∂r7∂u=fx∂r7∂d+fd∂r7∂x,∂r8∂u=fx∂r8∂d+fd∂r8∂x∂r3∂y=∂yc∂y∂r3∂yc,∂r4∂y=∂yc∂y∂r4∂yc,∂r5∂y=∂yc∂y∂r5∂yc,∂r6∂y=∂zc∂y∂r6∂zc,∂r7∂y=∂zc∂y∂r7∂zc,∂r8∂y=∂zc∂y∂r8∂zc∂r0∂v=fy∂r0∂d,∂r1∂v=fy∂r1∂d,∂r2∂v=fy∂r2∂d∂r3∂v=fy∂r3∂d+fd∂r3∂y,∂r4∂v=fy∂r4∂d+fd∂r4∂y,∂r5∂v=fu∂r5∂d+fd∂r5∂y∂r6∂v=fy∂r6∂d+fd∂r6∂y,∂r7∂v=fy∂r7∂d+fd∂r7∂y,∂r8∂v=fy∂r8∂d+fd∂r8∂y
5、计算关于三维点的偏导数 ∂ u ∂ X , ∂ u ∂ Y , ∂ u ∂ Z , ∂ v ∂ X , ∂ v ∂ Y , ∂ v ∂ Z \frac{\partial u}{\partial X},\frac{\partial u}{\partial Y},\frac{\partial u}{\partial Z},\frac{\partial v}{\partial X},\frac{\partial v}{\partial Y},\frac{\partial v}{\partial Z} ∂X∂u,∂Y∂u,∂Z∂u,∂X∂v,∂Y∂v,∂Z∂v
∂ x c ∂ X = r 0 , ∂ x c ∂ Y = r 1 , ∂ x c ∂ Z = r 2 ∂ y c ∂ X = r 3 , ∂ y c ∂ Y = r 4 , ∂ y c ∂ Z = r 5 ∂ z c ∂ X = r 6 , ∂ z c ∂ Y = r 7 , ∂ z c ∂ Z = r 8 ∂ x ∂ X = ∂ x ∂ x c ∂ x c ∂ X + ∂ x ∂ z c ∂ z c ∂ X , ∂ y ∂ X = ∂ y ∂ y c ∂ y c ∂ X + ∂ y ∂ z c ∂ z c ∂ X ∂ x ∂ Y = ∂ x ∂ x c ∂ x c ∂ Y + ∂ x ∂ z c ∂ z c ∂ Y , ∂ y ∂ Y = ∂ y ∂ y c ∂ y c ∂ Y + ∂ y ∂ z c ∂ z c ∂ Y ∂ x ∂ Z = ∂ x ∂ x c ∂ x c ∂ Z + ∂ x ∂ z c ∂ z c ∂ Z , ∂ y ∂ Z = ∂ y ∂ y c ∂ y c ∂ Z + ∂ y ∂ z c ∂ z c ∂ Z ∂ r 2 ∂ X = ∂ r 2 ∂ x ∂ x ∂ X + ∂ r 2 ∂ y ∂ y ∂ X , ∂ r 2 ∂ Y = ∂ r 2 ∂ x ∂ x ∂ Y + ∂ r 2 ∂ y ∂ y ∂ Y , ∂ r 2 ∂ Z = ∂ r 2 ∂ x ∂ x ∂ Z + ∂ r 2 ∂ y ∂ y ∂ Z ∂ d ∂ X = ∂ d ∂ r 2 ∂ r 2 ∂ X , ∂ d ∂ Y = ∂ d ∂ r 2 ∂ r 2 ∂ Y , ∂ d ∂ Z = ∂ d ∂ r 2 ∂ r 2 ∂ Z ∂ u ∂ X = f x ∂ d ∂ X + f d ∂ x ∂ X , ∂ u ∂ Y = f x ∂ d ∂ Y + f d ∂ x ∂ Y , ∂ u ∂ Z = f x ∂ d ∂ Z + f d ∂ x ∂ Z ∂ v ∂ X = f y ∂ d ∂ X + f d ∂ y ∂ X , ∂ v ∂ Y = f y ∂ d ∂ Y + f d ∂ y ∂ Y , ∂ v ∂ Z = f y ∂ d ∂ Z + f d ∂ y ∂ Z \begin{aligned} &\frac{\partial x_c}{\partial X} = r0,{\kern 10pt}\frac{\partial x_c}{\partial Y} = r1,{\kern 10pt}\frac{\partial x_c}{\partial Z} = r2 \\ &\frac{\partial y_c}{\partial X} = r3,{\kern 10pt}\frac{\partial y_c}{\partial Y} = r4,{\kern 10pt}\frac{\partial y_c}{\partial Z} = r5 \\ &\frac{\partial z_c}{\partial X} = r6,{\kern 10pt}\frac{\partial z_c}{\partial Y} = r7,{\kern 10pt}\frac{\partial z_c}{\partial Z} = r8 \\\\ &\frac{\partial x}{\partial X} = \frac{\partial x}{\partial x_c}\frac{\partial x_c}{\partial X}+\frac{\partial x}{\partial z_c}\frac{\partial z_c}{\partial X},{\kern 10pt}\frac{\partial y}{\partial X} = \frac{\partial y}{\partial y_c}\frac{\partial y_c}{\partial X}+\frac{\partial y}{\partial z_c}\frac{\partial z_c}{\partial X}\\ &\frac{\partial x}{\partial Y} = \frac{\partial x}{\partial x_c}\frac{\partial x_c}{\partial Y}+\frac{\partial x}{\partial z_c}\frac{\partial z_c}{\partial Y},{\kern 10pt}\frac{\partial y}{\partial Y} = \frac{\partial y}{\partial y_c}\frac{\partial y_c}{\partial Y}+\frac{\partial y}{\partial z_c}\frac{\partial z_c}{\partial Y}\\ &\frac{\partial x}{\partial Z} = \frac{\partial x}{\partial x_c}\frac{\partial x_c}{\partial Z}+\frac{\partial x}{\partial z_c}\frac{\partial z_c}{\partial Z},{\kern 10pt}\frac{\partial y}{\partial Z} = \frac{\partial y}{\partial y_c}\frac{\partial y_c}{\partial Z}+\frac{\partial y}{\partial z_c}\frac{\partial z_c}{\partial Z} \\\\ &\frac{\partial r^2}{\partial X} =\frac{\partial r^2}{\partial x}\frac{\partial x}{\partial X}+\frac{\partial r^2}{\partial y}\frac{\partial y}{\partial X},{\kern 10pt}\frac{\partial r^2}{\partial Y} =\frac{\partial r^2}{\partial x}\frac{\partial x}{\partial Y}+\frac{\partial r^2}{\partial y}\frac{\partial y}{\partial Y},{\kern 10pt}\frac{\partial r^2}{\partial Z} =\frac{\partial r^2}{\partial x}\frac{\partial x}{\partial Z}+\frac{\partial r^2}{\partial y}\frac{\partial y}{\partial Z}\\\\ &\frac{\partial d}{\partial X} = \frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial X},{\kern 10pt}\frac{\partial d}{\partial Y} = \frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial Y},{\kern 10pt}\frac{\partial d}{\partial Z} = \frac{\partial d}{\partial r^2}\frac{\partial r^2}{\partial Z}\\ &\color{red}\frac{\partial u}{\partial X} = fx\frac{\partial d}{\partial X}+ fd\frac{\partial x}{\partial X},{\kern 10pt}\frac{\partial u}{\partial Y} = fx\frac{\partial d}{\partial Y}+ fd\frac{\partial x}{\partial Y} ,{\kern 10pt}\frac{\partial u}{\partial Z} = fx\frac{\partial d}{\partial Z}+ fd\frac{\partial x}{\partial Z}\\ &\color{red}\frac{\partial v}{\partial X} = fy\frac{\partial d}{\partial X}+ fd\frac{\partial y}{\partial X},{\kern 10pt}\frac{\partial v}{\partial Y} = fy\frac{\partial d}{\partial Y}+ fd\frac{\partial y}{\partial Y} ,{\kern 10pt}\frac{\partial v}{\partial Z} = fy\frac{\partial d}{\partial Z}+ fd\frac{\partial y}{\partial Z} \end{aligned} ∂X∂xc=r0,∂Y∂xc=r1,∂Z∂xc=r2∂X∂yc=r3,∂Y∂yc=r4,∂Z∂yc=r5∂X∂zc=r6,∂Y∂zc=r7,∂Z∂zc=r8∂X∂x=∂xc∂x∂X∂xc+∂zc∂x∂X∂zc,∂X∂y=∂yc∂y∂X∂yc+∂zc∂y∂X∂zc∂Y∂x=∂xc∂x∂Y∂xc+∂zc∂x∂Y∂zc,∂Y∂y=∂yc∂y∂Y∂yc+∂zc∂y∂Y∂zc∂Z∂x=∂xc∂x∂Z∂xc+∂zc∂x∂Z∂zc,∂Z∂y=∂yc∂y∂Z∂yc+∂zc∂y∂Z∂zc∂X∂r2=∂x∂r2∂X∂x+∂y∂r2∂X∂y,∂Y∂r2=∂x∂r2∂Y∂x+∂y∂r2∂Y∂y,∂Z∂r2=∂x∂r2∂Z∂x+∂y∂r2∂Z∂y∂X∂d=∂r2∂d∂X∂r2,∂Y∂d=∂r2∂d∂Y∂r2,∂Z∂d=∂r2∂d∂Z∂r2∂X∂u=fx∂X∂d+fd∂X∂x,∂Y∂u=fx∂Y∂d+fd∂Y∂x,∂Z∂u=fx∂Z∂d+fd∂Z∂x∂X∂v=fy∂X∂d+fd∂X∂y,∂Y∂v=fy∂Y∂d+fd∂Y∂y,∂Z∂v=fy∂Z∂d+fd∂Z∂y
代码实现
https://github.com/ldx-star/Bundle-Adjustment
这篇关于【三维重建】捆绑调整的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








