本文主要是介绍LOF(局部离群因子)异常值检测,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
LOF(Local Outlier Factor,局部离群因子)异常值检测的原理和实现步骤时,我们可以进一步详细解释如下:

原理
LOF算法基于密度的概念来判断数据集中的异常点。它比较每个数据点与其邻近点的局部密度,以确定该点是否异常。如果一个点的局部密度明显低于其邻近点,则它被视为异常点。
LOF算法的关键在于“局部”的概念,这意味着它考虑了数据点的邻近区域,而不是全局数据集。这使得LOF算法能够识别局部异常点,即使它们在整个数据集中的位置并不异常。
实现步骤
- 计算k距离(k-distance):
- 对于数据集中的每个点p,找到距离它最近的k个点的最大距离,这个距离就是p的k距离。
- k距离表示了p的邻域大小。
- 计算k距离邻域(k-distance neighborhood):
- 对于数据集中的每个点p,找到所有距离p不超过其k距离的点,这些点组成的集合就是p的k距离邻域。
- 计算可达距离(Reachability Distance):
- 对于点p和其k距离邻域中的点o,p关于o的可达距离定义为o的k距离和p与o之间的实际距离中的较大值。
- 可达距离用于避免距离p很近但k距离很大的点对p的局部密度产生过大的影响。
- 计算局部可达密度(Local Reachability Density,LRD):
- 对于点p,其局部可达密度是其k距离邻域中所有点关于p的可达距离之和的倒数,再除以k。
- 局部可达密度越高,说明p的邻域点越密集,p越可能是正常点。
- 计算局部离群因子(Local Outlier Factor,LOF):
- 对于点p,其LOF是其k距离邻域中所有点的局部可达密度与p的局部可达密度的比值的平均值。
- 如果LOF接近1,说明p的密度与其邻域点相似,p是正常点;如果LOF远大于1,说明p的密度明显低于其邻域点,p是异常点。
- 异常检测:
- 根据LOF值,设定一个阈值来判断哪些点是异常点。通常,LOF值大于某个阈值的点被认为是异常点。
注意事项
- k值的选择对LOF算法的结果有很大影响。k值太小可能导致误报(将正常点误判为异常点),k值太大可能导致漏报(漏掉一些真正的异常点)。
- LOF算法对高维数据可能不太有效,因为高维空间中点的距离度量可能不太准确。
- LOF算法的计算复杂度较高,对于大规模数据集可能需要较长的计算时间。
实际应用
LOF算法在欺诈检测、网络安全、工业监测等领域都有广泛的应用。例如,在信用卡欺诈检测中,LOF算法可以帮助识别出与正常交易模式显著不同的异常交易。在网络安全领域,LOF算法可以用于检测网络流量中的异常模式,从而识别出可能的网络攻击。
部分代码展示
function lof = LOF(dist,K)
m=size(dist,1); %m为对象数,dist为两两之间的距离
distance = zeros(m,m);
num = zeros(m,m); %distance 和num用来记录排序后的顺序,和对象编号顺序
kdistance = zeros(m,1); %计算每个对象的kdistance
count = zeros(m,1); %k邻域的对象数
reachdist = zeros(m,m); %计算两两之间的reachable-distance
lrd = zeros(m,1);
lof = zeros(m,1);
%计算k-距离
for i=1:m[distance(i,:),num(i,:)]=sort(dist(i,:),'ascend');kdistance(i)=distance(i,K+1); count(i) = -1;%自己的距离为0,要去掉自己for j = 1:mif dist(i,j)<=kdistance(i)count(i) = count(i)+1;endend
end
for i = 1:mfor j=1:i-1reachdist(i,j) = max(dist(i,j),kdistance(j));reachdist(j,i) = reachdist(i,j);end数据集格式为excel
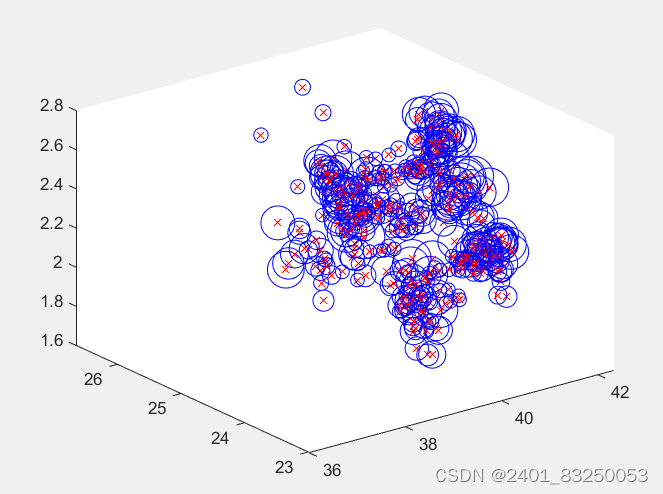
结果图

这篇关于LOF(局部离群因子)异常值检测的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




