本文主要是介绍2024五一杯数学建模B题思路代码文章教学-交通需求规划与可达率问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
交通需求规划与可达率问题
问题总结:
问题一:在一个小型交通网络中,给定的起点和终点之间的交通需求需分配到相应路径上。目标是最大化任意一条路段出现突发状况时的交通需求期望可达率。
问题二:在一个较大的交通网络中,同样需分配交通需求至特定路径,但要考虑到同时有五条路段出现突发状况的情况。 概率模型
问题三:在同一个较大的交通网络中,除了考虑五条路段同时出现突发状况外,还需考虑路段的容量上限,确保任何路段的交通量不超过其容量。
问题四:此问题涉及在现有网络中新建六条路段,以优化在任意五条路段出现突发情况时的可达率。需要确定新建路段的起点和终点,同时确保这些路段不跨越其他路段。
详细问题分析:
问题一:小型交通网络的需求分配
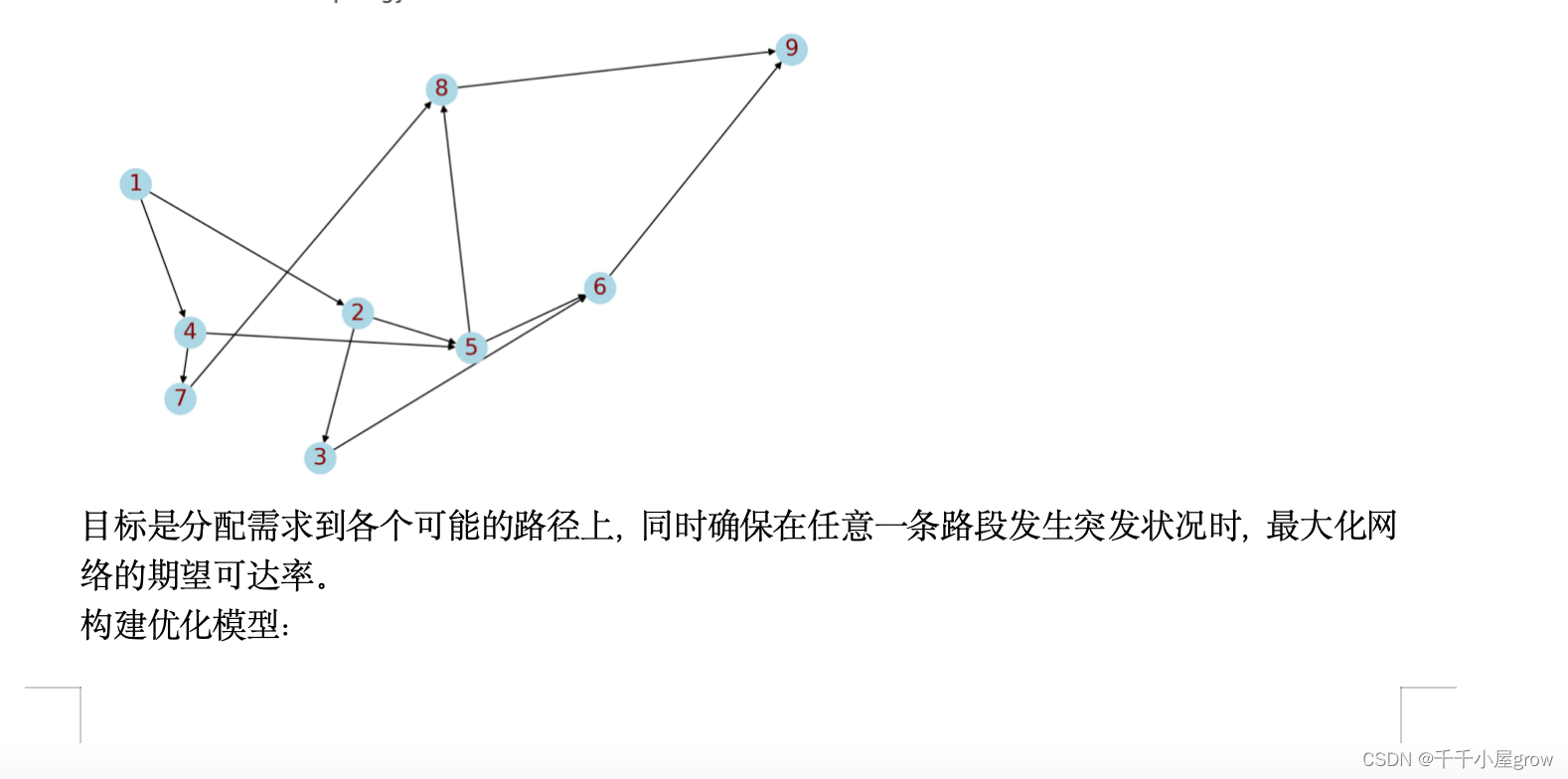
目标是分配需求到各个可能的路径上,同时确保在任意一条路段发生突发状况时,最大化网络的期望可达率。
构建优化模型:
确定所有可能的路径:对于每个起点和终点对,找出所有可能的路径。
定义变量:设xij 为从节点 i 到节点 j 的交通流量。
目标函数:最大化期望可达率,即最小化因单条路段故障导致的需求未满足的总量。
约束条件:
每对起点和终点之间的总流量应满足需求量。
流量非负性。
使用SciPy库中的优化工具来实现。
首先,让我们为每个起点和终点对确定所有可能的路径,并设置决策变量。
对于第一个起点和终点对(从1到5),我们找到了两条可能的路径:[1, 2, 5]和 [1, 4, 5]。这些路径将用于我们的流量分配模型。接下来,我们将定义决策变量和模型的目标函数。
我们将每条路径上的流量作为决策变量,并构建目标函数以最大化期望可达率。这将通过最小化由于任意单一路段故障可能造成的总未满足需求量来实现。为此,我们需要考虑每条路径对每条路段的贡献,以及每条路段的故障对总需求满足情况的影响。

问题二:较大交通网络的需求分配
目标:
与问题一类似,但需要考虑同时有五条路段出现突发情况。
模型思路:
随机性考虑:每个路段出现突发状况的概率相同,使用概率模型来估计多条路段同时出现突发状况的影响。
优化方法:可能需要采用随机优化或模拟退火等高级算法来求解。
问题三:考虑路段容量的需求分配
目标:
在问题二的基础上,增加路段容量的约束,保证任何时候各路段的交通量不超过其上限。
模型思路:
非线性约束:加入容量限制后,问题可能转为非线性规划问题。
多目标优化:可能需要同时考虑最大化可达率和最小化路段使用频率等多重目标。
问题四:新建路段的优化配置
目标:
在考虑到突发事故情况下,通过新增路段优化网络的可达率。
模型思路:
网络设计:基于现有网络,识别可能的新增路段位置。
优化模型:使用图的修改算法来评估新路段对整体网络性能的提升效果。
#【腾讯文档】2024五一杯助攻合集
# https://docs.qq.com/doc/DVU1pc1VmZVZXS29J
这篇关于2024五一杯数学建模B题思路代码文章教学-交通需求规划与可达率问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







