西瓜书学习——决策树形状、熵和决策树的本质

本文主要是介绍西瓜书学习——决策树形状、熵和决策树的本质，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

决策树形状

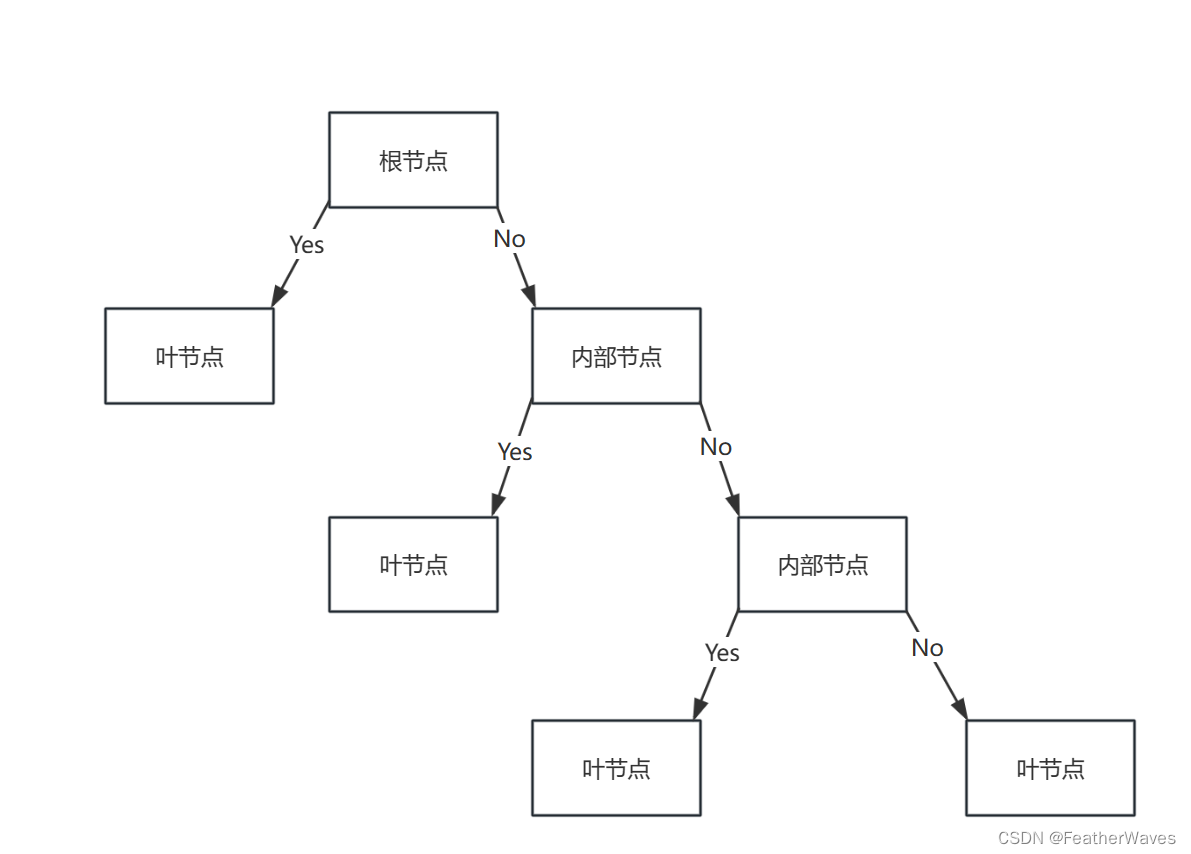
内部节点：每个内部节点代表一个特征属性。在决策树构建过程中，根据某种准则（如信息增益、基尼不纯度等）选择最优的特征属性作为节点的判断标准。数据集在每个内部节点处根据特征属性的取值被分割成子集，从而实现了数据的划分。

叶子节点：每个叶子节点代表一个决策结果。在分类任务中，叶子节点通常表示一个类别标签，而在回归任务中，叶子节点表示一个连续的输出值。叶子节点的决策结果是通过训练数据集上的多数投票（分类）或平均值（回归）得到的。

监督学习算法

决策树是一种监督学习算法，因为它需要带有标签的训练数据集来构建模型。在训练过程中，决策树算法学习如何根据输入特征来预测输出标签。

分类与回归

• 分类树：用于分类任务的决策树。每个叶子节点代表一个类别，模型的输出是预测数据点属于哪个类别。
• 回归树：用于回归任务的决策树。每个叶子节点代表一个连续值，模型的输出是预测数据点的连续值。

无论是分类还是回归，决策树都是通过递归地划分数据集来构建的。在分类树中，通常使用信息增益、增益率或基尼不纯度来选择最优的特征属性；而在回归树中，通常使用最小二乘回归树的方法来选择最优的特征属性和分割点。

决策树的一个优点是它们易于理解，因为它们的决策过程可以通过可视化来直观展示。然而，决策树也容易过拟合，特别是当树的结构非常深时。为了避免过拟合，可以采用剪枝技术，如预剪枝和后剪枝，来限制树的复杂度。此外，决策树的一个变体是随机森林，它通过集成多个决策树来提高模型的泛化能力。

熵

信息熵

信息熵可以理解为信息含量的度量，熵越高，信息含量越大，不确定性也越大。对于离散随机变量，其熵可以通过以下公式计算：

$$H(X)=-\sum _{i=1}^{n}p(x_i){\log }_{b}p(x_i)$$

其中，$H(X)$ 是随机变量 $X$ 的熵，$p(x_i)$ 是随机变量 $X$ 取值为 $x_i$ 的概率，$n$是随机变量 $X$ 的所有可能取值的个数，$b$ 是计算熵时使用的底数，通常取 2、e或 10，分别对应于以比特、纳特或十特为单位的熵。

假设我们有一个公平的六面骰子。我们想要知道掷骰子时得到的信息量。每个面出现的概率都是 1/6，因此我们可以计算这个随机事件的熵。

首先，我们选择以2为底数（这样可以计算以比特为单位的熵），然后应用熵的公式：

$$H(X)=-\sum _{i=1}^{6}p(x_i){\log }_{2}p(x_i)$$

其中 $p(x_i)=1/6$ 对于所有的 $i$（因为每个面出现的概率是相等的）。
$$\begin{gathered} H(X)=-6\times \frac{1}{6}{\log }_2\frac{1}{6} \\ H(X)=-{\log }_2\frac{1}{6} \\ H(X)={\log }_{2}6 \\ H(X)\approx 2.585 \end{gathered}$$

所以，一个公平的六面骰子的信息熵大约是 2.585 比特。这意味着每次掷骰子时，你得到的信息量大约是 2.585 比特。

现在，如果我们考虑一个不公平的骰子，其中某个面出现的概率更高，那么这个面的信息量就会减少（因为你已经预期它更可能出现），从而降低整个系统的熵。相反，如果所有面出现的概率相等，熵就会更高，因为每个结果都是同样不可预测的。

香农熵 (Shannon Entropy) - H(X)

香农熵是衡量单个随机变量不确定性的度量。对于离散随机变量 $X$，其香农熵定义为：

$$H(X)=-\sum _{i}p(x_i){\log }_{b}p(x_i)$$

其中，$p(x_i)$是随机变量 X 取值为$x_i$的概率，$b$是底数（通常取 2、e 或 10）。

联合熵 (Joint Entropy) - H(X, Y)

联合熵是衡量两个或多个随机变量共同发生的不确定性的度量。对于两个随机变量 $X$ 和 $Y$，其联合熵定义为：

$$H(X,Y)=-\sum _{x,y}p(x,y){\log }_{b}p(x,y)$$

其中，$p(x,y)$是 $X$ 和 $Y$ 同时取值为$x$和$y$的联合概率。

条件熵 (Conditional Entropy) - H(Y|X)

条件熵是在已知一个随机变量的情况下，另一个随机变量的不确定性的度量。对于随机变量 $Y$ 在已知 $X$ 的情况下的条件熵定义为：

$$H(Y|X)=\sum _{x}p(x)H(Y|X=x)$$

其中，$H(Y|X=x)$是在 $X$ 取值为 $x$ 的条件下 $Y$的条件熵。

互信息 (Mutual Information) - I(X; Y)

互信息是衡量两个随机变量之间相互依赖性的度量。互信息定义为：

$$I(X;Y)=H(Y)-H(Y|X)$$

互信息也可以表示为联合熵和单独熵的差：

$$I(X;Y)=H(X)+H(Y)-H(X,Y)$$

相对熵 (Relative Entropy) / KL散度 (Kullback-Leibler Divergence) - DKL(P||Q)

相对熵，也称为KL散度，是衡量两个概率分布之间差异的度量。对于两个概率分布 $P$ 和 $Q$，KL散度定义为：

$$D_{KL}(P||Q)=\sum _{i}P(i)\log \frac{P(i)}{Q(i)}$$

KL散度是非负的，并且不是对称的，即$D_{KL}(P||Q)\ne D_{KL}(Q||P)$。

交叉熵 (Cross-Entropy) - H(P, Q)

交叉熵是衡量两个概率分布之间差异的另一种度量。对于概率分布 $P$ 和 $Q$，交叉熵定义为：

$$H(P,Q)=-\sum _{i}P(i)\log Q(i)$$

交叉熵可以用来衡量 $Q$ 分布与 $P$ 分布之间的差异。

相互关系

• 互信息 $I(X;Y)$ 可以看作是 $X$ 和 $Y$ 共享的信息量，或者是在知道 $X$ 的值后 $Y$ 的不确定性的减少量。

• 条件熵 $H(Y|X)$ 可以通过香农熵 $H(Y)$ 减去互信息 $I(X;Y)$ 来计算。

• KL散度 $DKL(P||Q)$ 可以通过交叉熵 $H(P,Q)$ 减去 $P$ 的熵 $H(P)$ 来计算。

这些熵和散度在机器学习、数据科学和通信理论中有着广泛的应用，用于量化不确定性、优化模型、评估模型性能以及比较概率分布。

H(Y) 和 H(Y|X)

H(Y)

$H(Y)$ 是随机变量 $Y$ 的无条件熵，它衡量的是 $Y$ 本身的不确定性。换句话说，$H(Y)$ 告诉我们在没有任何其他信息的情况下，随机变量 $Y$ 的取值有多么不可预测。无条件熵越大，$Y$ 的取值就越分散，我们也就越难准确预测 Y 的具体取值。

$H(Y)$ 的计算公式是：

$$H(Y)=-\sum _{y\in Y}p(y){\log }_{b}p(y)$$

其中，$p(y)$ 是随机变量 $Y$ 取值为 $y$ 的概率，$b$ 是计算熵时使用的底数（通常取 2、e 或 10）。

H(Y|X)

$H(Y|X)$ 是在已知随机变量 $X$ 的取值的情况下，随机变量 $Y$ 的条件熵。它衡量的是在已经知道 $X$ 的信息后，$Y$ 的不确定性还有多少。如果 $X$ 和 $Y$ 完全独立，那么知道 $X$ 的取值不会对 $Y$ 的不确定性产生影响，$H(Y|X)$ 将等于 $H(Y)$。如果 $X$ 和 $Y$ 完全相关，那么一旦知道了 $X$ 的取值，$Y$ 的取值也就确定了，此时 $H(Y|X)$ 将为 0。

$H(Y|X)$ 的计算公式是：

$$H(Y|X)=\sum _{x\in X}p(x)H(Y|X=x)$$

其中，$p(x)$ 是随机变量 $X$ 取值为 $x$ 的概率，$H(Y|X=x)$ 是在 $X$ 取值为 $x$ 的条件下 $Y$ 的条件熵，其计算公式为：

$$H(Y|X=x)=-\sum _{y\in Y}p(y|x){\log }_{b}p(y|x)$$

其中，$p(y|x)$ 是在 $X$ 取值为 $x$ 的条件下，$Y$ 取值为 $y$ 的条件概率。

理解关系

$H(Y)$ 和 $H(Y|X)$ 之间的关系可以通过互信息 $I(X;Y)$ 来理解，互信息衡量的是知道 $X$ 的值后 $Y$ 的不确定性的减少量。互信息 $I(X;Y)$ 可以表示为：

$$I(X;Y)=H(Y)-H(Y|X)$$

这也可以写作：

$$I(X;Y)=H(Y)-H(Y|X)=H(X)+H(Y)-H(X,Y)$$

互信息 $I(X;Y)$ 描述了知道 $X$ 的值后 $Y$ 的不确定性的减少量。如果 $X$ 和 $Y$ 完全独立，那么 $I(X;Y)=0；$如果 $X$ 和 $Y$ 完全相关，那么 $I(X;Y)=H(Y)$。

决策树的本质

损失函数：总信息熵

决策树的构建是一个递归的过程，每次选择最优的特征来分割数据集，直到满足停止条件。在这个过程中，我们需要一个准则来衡量分割的好坏，这个准则就是损失函数。在决策树中，常用的损失函数是总信息熵（Overall Information Entropy），它衡量的是数据集的不确定性。我们希望每次分割都能最大程度地减少数据集的不确定性，从而提高模型的预测准确性。

信息熵是由香农提出的，用于衡量一个随机变量的不确定性。在决策树中，我们通常使用信息熵来衡量数据集的不确定性。数据集的信息熵定义为：

$$H(D)=-\sum _{i=1}^n{p}_i{\log }_2{p}_i$$

其中，$p_i$ 是数据集中第 $i$ 类样本的比例。信息熵越大，数据集的不确定性越高。

梯度：信息增益

在机器学习中，梯度是损失函数的导数，它指向损失函数增加最快的方向。在决策树中，我们没有显式的梯度概念，但可以类比地引入“梯度”的概念，即信息增益（Information Gain），它衡量的是分割前后数据集信息熵的减少量。我们希望每次分割都能获得最大的信息增益，从而最大程度地减少数据集的不确定性。

信息增益的计算公式为：

$$IG(D,A)=H(D)-\sum _{j=1}^m\frac{|D_j|}{|D|}H(D_j)$$

其中，$H(D)$是数据集 D的信息熵，$D_j$是数据集 $D$ 在特征 $A$ 的第 $j$ 个取值下的子集，$|D_j|$是子集 $D_j$的样本数，$|D|$是数据集 $D$的样本数。

决策树：梯度下降路径

在构建决策树的过程中，我们每次选择最优的特征来分割数据集，这可以类比于梯度下降算法中的迭代优化过程。在梯度下降中，我们沿着梯度的反方向更新参数，以减小损失函数的值。

在决策树中，我们选择信息增益最大的特征进行分割，这可以看作是在沿着信息熵减少的方向优化，即“梯度下降路径”。

非参数模型

决策树是一种非参数模型，这意味着它不依赖于数据的分布假设，可以捕捉数据中的非线性关系。决策树的灵活性使得它适用于多种数据类型和任务，但它也容易过拟合，因此需要剪枝等技术来提高模型的泛化能力。

总结来说，决策树的本质是一种基于总信息熵的损失函数，通过信息增益来选择最优特征进行分割的梯度下降路径，它是一种灵活的非参数模型，可以捕捉数据中的复杂关系。

这篇关于西瓜书学习——决策树形状、熵和决策树的本质的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---