本文主要是介绍leetcode51.N皇后(困难)-回溯法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!


思路
都知道n皇后问题是回溯算法解决的经典问题,但是用回溯解决多了组合、切割、子集、排列问题之后,遇到这种二维矩阵还会有点不知所措。
首先来看一下皇后们的约束条件:
- 不能同行
- 不能同列
- 不能同斜线
确定完约束条件,来看看究竟要怎么去搜索皇后们的位置,其实搜索皇后的位置,可以抽象为一棵树。
下面我用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如图:
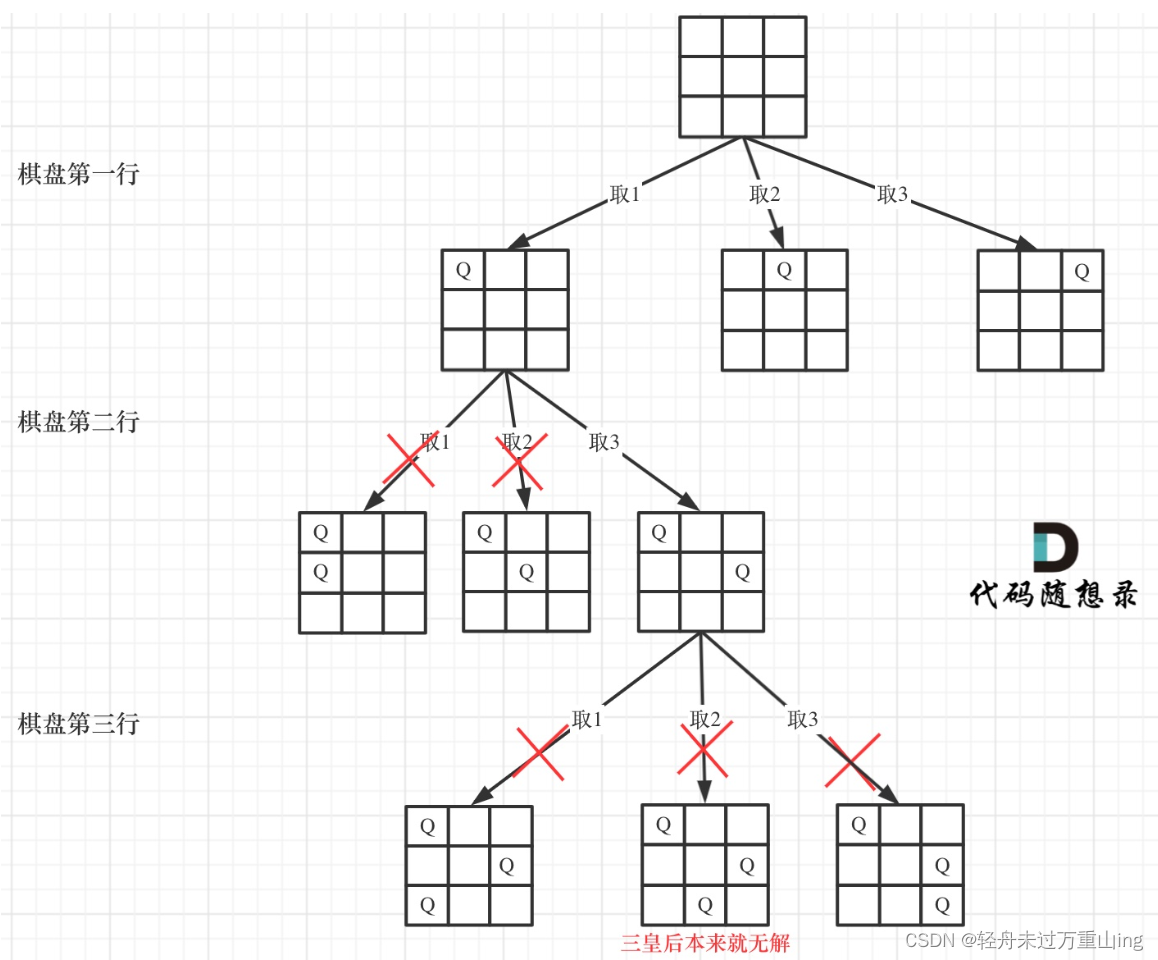
从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
那么我们用皇后们的约束条件,来回溯搜索这棵树,只要搜索到了树的叶子节点,说明就找到了皇后们的合理位置了。
然后套用递归三部曲解决。
- 递归函数参数
- 递归终止条件
- 单层搜索的逻辑
这里还要外加一个 :验证棋盘是否合法
按照如下标准去重:
- 不能同行
- 不能同列
- 不能同斜线 (45度和135度角)
java版本代码:
class Solution {List<List<String>> res = new ArrayList<>(); //全局变量res集合,用于存储解决方案的列表// 解决N皇后问题的方法,返回解决方案的集合public List<List<String>> solveNQueens(int n) {char[][] chessboard = new char[n][n]; // 创建一个N*N的字符棋盘for (char[] c : chessboard) {Arrays.fill(c, '.'); // 初始化棋盘,填充为'.'}backTrack(n, 0, chessboard); // 调用回溯方法,开始搜索解决方案return res; // 返回所有解决方案的集合}// 回溯方法,用于搜索解决N皇后问题的解决方案// n 为输入的棋盘大小// row 是当前递归到棋盘的第几行了public void backTrack(int n, int row, char[][] chessboard) {if (row == n) { // 终止条件:如果已经填满了所有行,即找到了一种解决方案res.add(Array2List(chessboard)); // 将当前棋盘状态添加到解决方案的集合中(list集合里的元素还是个集合list,见示例)return;}for (int col = 0; col < n; ++col) { // 遍历当前行的所有列if (isValid(row, col, n, chessboard)) { // 如果当前位置可以放置皇后chessboard[row][col] = 'Q'; // 放置皇后backTrack(n, row + 1, chessboard); // 递归搜索下一行的解决方案chessboard[row][col] = '.'; // 回溯,撤销当前位置的皇后(把Q替换成 .即可)}}}// 将二维字符数组转换为字符串集合public List Array2List(char[][] chessboard) {List<String> list = new ArrayList<>(); // 创建一个空集合for (char[] c : chessboard) { // 遍历棋盘的每一行 字符数组:char[] c,eg:{"Q",".",".",".",} 、list.add(String.copyValueOf(c)); // 将当前行的字符数组char[] c 转换为字符串并添加到集合list中}return list; // 返回转换后的集合 eg:[".Q..","...Q","Q...","..Q."]}// 检查当前位置是否可以放置皇后isValid()方法 :从上往下去找的,所以对角线只找了左上和右上public boolean isValid(int row, int col, int n, char[][] chessboard) {// 检查同一列是否已经放置了皇后for (int i = 0; i < row; ++i) { // 遍历当前列之前的所有行if (chessboard[i][col] == 'Q') { // 如果当前位置上方有皇后return false; // 返回false,表示当前位置不能放置皇后}}// 检查45度对角线上是否已经放置了皇后for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) { // 向左上方遍历if (chessboard[i][j] == 'Q') { // 如果当前位置左上方有皇后return false; // 返回false,表示当前位置不能放置皇后}}// 检查135度对角线上是否已经放置了皇后for (int i = row - 1, j = col + 1; i >= 0 && j <= n - 1; i--, j++) { // 向右上方遍历if (chessboard[i][j] == 'Q') { // 如果当前位置右上方有皇后return false; // 返回false,表示当前位置不能放置皇后}}return true; // 如果以上条件都不满足,表示当前位置可以放置皇后,返回true}
}
这篇关于leetcode51.N皇后(困难)-回溯法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






