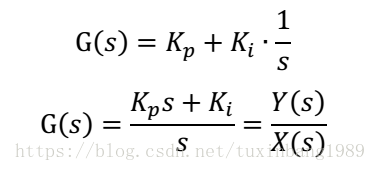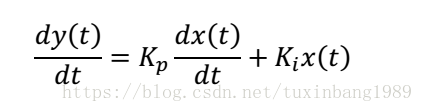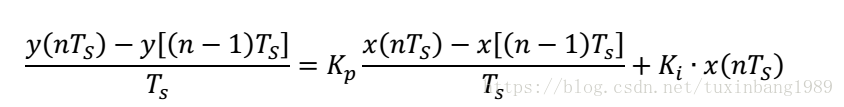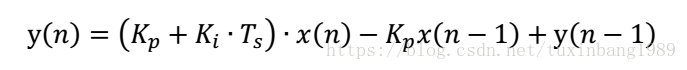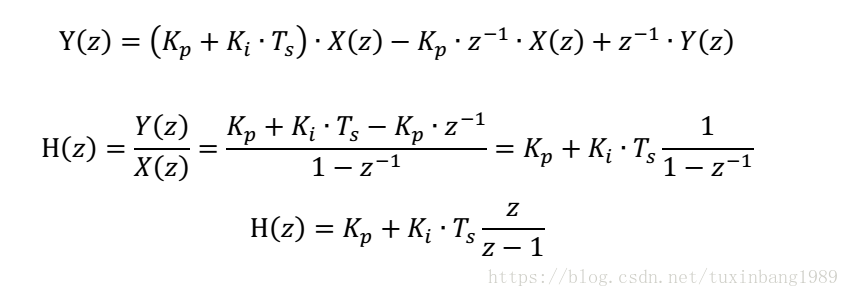本文主要是介绍PI校正环节的程序实现推导过程,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
PI校正环节在经典控制论中非常有用,特别是对负反馈控制系统,基本上都有PI校正环节。
1.下面分别说明比例环节和积分环节的作用,以阶跃信号为例。
①比例环节单独作用
以上分析说明,若只有比例环节的控制系统,阶跃响应也是一个阶跃信号,但会存在一定静差,且静差值随Kp增大而减小,但始终存在,不随时间变化。
输出的理论波形跟实际的数字控制输出波形会不一致。因为实际数字控制系统每隔一个计算周期运算一次,而在这个计算周期中,输出量只受上一次的调节参数和中间变量的控制。所以可能会出现超调情况。
②比例-积分共同作用
拉氏反变换
以上分析说明,当加入积分项后,阶跃响应为一逐渐上升的曲线,且误差分量随时间逐渐趋于零;KI越大,误差分量衰减越快,KP越大,误差分量衰减越慢。
PI校正环节的优缺点:
比例系数Kp增大,则会减小稳态误差,减小了上升时间,提高了响应速度,但会引入并逐渐增大超调量,直至系统振荡;
积分环节提高了系统型别,消除稳态误差,但参数KI若过大,积分作用太强,会在大偏差阶段引起过大超调,调节时间变长,最后振荡。
2.PI环节的表达式
传递函数
微分方程
对应的离散方程为
写成序列形式
写出相应的 z 变换系统方程
根据序列形式,可以写出程序代码:
#define Ts 0.00001 // 采样时间
typedef struct PI_Ele{float kp; // 比例环节系数float ki; // 积分环节系数float x1;float x2;float yout;float y1;
} PI_Vector;
#define PI_Macro(PI_Vector v) \ // 算法的宏定义v.yout = (v.kp+v.ki*Ts)*v.x2-v.kp*x1+v.y1; \v.x1 = v.x2; \v.y1 = v.yout;
这篇关于PI校正环节的程序实现推导过程的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!